PCl点云学习十（PFH、FPFH、VFH直方图描述子）

来源：pcl官网

PFH

1. 简介

• 局部点的法线和曲率不能对应唯一的点

2. 理论准备

• 使用目标点k临近区域内的邻域点，通过归一化曲率和法线，并对其进行编码，构建多维直方图
• 多维直方图包含不变的6维姿态、邻域点不同的采样频率、不同水平的噪声
• 术语
  $p_q:$待查询点，红色的点
  $r:$半径
  $k:$邻域点的个数并且全在半径r内，相互之间互相连接
  通过计算邻域点内k个点对之间的直方图，得到PFH描述子，最终计算复杂度为$O(k^2)$
  
• 计算两点之间$p_i,p_j$之间的法线$n_i,n_j$，在其中一个点上定义一个固定坐标系($uvw$坐标系)，存在如下关系：
  $$\begin{gathered} u=n_s \\ v=u\times \frac{p_t-p_s}{||p_t-p_s|{|}_2} \\ w=u\times v \end{gathered}$$
  法线$n_s$与$n_t$之间的法线之差可以表示为一组角度：

$$\{\begin{array}{l}\alpha =v\ast n_t\\ \varphi =u\ast \frac{p_t-p_s}{d}\\ \theta =\arctan (w\ast n_t,u\ast n_t)\\ d=||p_t-p_s||\end{array}$$
每个点对可以得到一组4个值$<\alpha ,\varphi ,\theta ,d>$，将所有4元组合并到直方图，每一维划分为b个子区域，统计临近点落在子区域的次数,得到$b^4$个直方图，在2.5数据集中最好忽略$d$维时

• pcl中每维数据使用5个区间，默认不使用$d$维
  

3. pcl中代码

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace pcl;
using namespace std;
int main(int argc, const char **argv)
{
    PointCloud<PointXYZ>::Ptr cloud(new PointCloud<PointXYZ>());
    PointCloud<Normal>::Ptr normals(new PointCloud<Normal>());
    PointCloud<PointXYZ>::Ptr cloudNan(new PointCloud<PointXYZ>());
    PointCloud<Normal>::Ptr normalsNan(new PointCloud<Normal>());
    PointCloud<PFHSignature125>::Ptr cloudPFH(new PointCloud<PFHSignature125>());

    pcl::io::loadPCDFile("/home/n1/notes/pcl/PFH/test.pcd", *cloud);
    pcl::NormalEstimation<PointXYZ, Normal> ne; //创建法线滤波器
    ne.setInputCloud(cloud);
    pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>());
    ne.setSearchMethod(tree); //设置搜索方法

    ne.setRadiusSearch(0.01); //设置搜索半径
    ne.compute(*normals);
    std::vector<int> indices; //处理无效值
    //pcl::removeNaNFromPointCloud(normals,normals,indices);//剔除无效数据

    //剔除无效点
    for (int i = 0; i < normals->size(); i++)
    {
        if (pcl::isFinite<pcl::Normal>((*normals)[i]))
        {
            // PCL_WARN("normals[%d] is finite\n", i);
            continue;
        }
        cloudNan->push_back(cloud->points[i]);
        normalsNan->push_back(normals->points[i]);
    }
    cloudNan->points.resize (cloudNan->width * cloudNan->height);
    normalsNan->points.resize (normalsNan->width * normalsNan->height);
    cout<<"size:"<<cloudNan->size()<<endl;
    pcl::PFHEstimation<PointXYZ,Normal,PFHSignature125> pfh;
    pfh.setInputCloud(cloudNan);
    pfh.setInputNormals(normalsNan);
    pcl::search::KdTree<pcl::PointXYZ>::Ptr pfhtree (new pcl::search::KdTree<pcl::PointXYZ> ());
    pfh.setSearchMethod(pfhtree);
    pfh.setRadiusSearch(0.03);
    pfh.compute(*cloudPFH);
        cout<<"cloudPFH size:"<<cloudPFH->size()<<endl;
    boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer(new pcl::visualization::PCLVisualizer("3D Viewer"));
    viewer->setBackgroundColor(0.0, 0.0, 0.0);
    viewer->addPointCloudNormals<pcl::PointXYZ, pcl::Normal>(cloud, normals);
    while (!viewer->wasStopped())
    {
        viewer->spinOnce();
    }
    return 0;
}

来自

FPFH(fast Point Feature Histograms)

简化了直方图，使其计算复杂度从$O(n{k}^2)$降低到$O(nk)$

• 4.1 步骤一：计算Pq和它邻域点之间（查询点与临近点）$\alpha ,\beta ,\theta$，记为$SPFH$值
  $$\{\begin{array}{l}\alpha =v\ast n_t\\ \varphi =u\ast \frac{p_t-p_s}{d}\\ \theta =\arctan (w\ast n_t,u\ast n_t)\\ d=||p_t-p_s||\end{array}$$

• 4.2 步骤二：重新计算每个点的k邻域，使用临近点的SPFH值来代替直方图：
  $w_k:$权重为查询点与邻域点之间的距离
  $$FPFH(P_q)=SPFH(P_q)+\frac{1}{k}\sum _{i=1}^k\frac{1}{w_k}\ast SPFH(P_k)$$

• 4.3 可以实时提取，论文中的步骤如下：
  

• 4.4 pcl中代码:
  核心代码，替他同PFH

    pcl::FPFHEstimation<PointXYZ,Normal,FPFHSignature33> fpfh;
    fpfh.setInputCloud(cloudNan);
    fpfh.setInputNormals(normalsNan);
    pcl::search::KdTree<pcl::PointXYZ>::Ptr fpfhtree (new pcl::search::KdTree<pcl::PointXYZ> ());
    fpfh.setSearchMethod(fpfhtree);
    fpfh.setRadiusSearch(0.03);//必须大于法线半径
    fpfh.compute(*cloudFPFH);

VFH(viewpoint feature Histogram)

官网
用作聚类或者6维位姿估计

1. 理论
   VFH源于FPFH，因为FPFH描述子便于识别，但是起步不具有伸缩不变性，所以在FPFH上添加视角点，以保持其尺度不变性。
   视角点方向的计算与FPFH中计算相对法线时同时进行
2. 如何计算
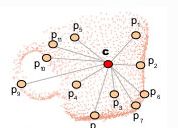
   2.1 收集视角点与每个法线的夹角作为直方图来计算视点分量。（将法线平移到的几何中心点与视角点构成的夹角）
   c：几何中心点
   2.2 计算FPFH的参数$\alpha ,\varphi ,\theta$
   
   3.源代码

#include 
#include 
#include 
#include 
#include 
#include 
using namespace pcl;
using namespace std;
using namespace pcl::visualization;
int main(int argc, const char** argv) {
    PCLPlotter *plotter = new PCLPlotter("My Plotter");
    PointCloud<PointXYZ>::Ptr cloud(new PointCloud<PointXYZ>());
    PointCloud<Normal>::Ptr normals(new PointCloud<Normal>());
    PointCloud<PointXYZ>::Ptr cloudNan(new PointCloud<PointXYZ>());
    PointCloud<Normal>::Ptr normalsNan(new PointCloud<Normal>());
    PointCloud<VFHSignature308>::Ptr cloudVFH(new PointCloud<VFHSignature308>());

    pcl::io::loadPCDFile("/home/n1/notes/pcl/VFH/test.pcd", *cloud);
    pcl::NormalEstimation<PointXYZ, Normal> ne; //创建法线滤波器
    ne.setInputCloud(cloud);
    pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>());
    ne.setSearchMethod(tree); //设置搜索方法

    ne.setRadiusSearch(0.01); //设置搜索半径
    ne.compute(*normals);


    //剔除无效点
    for (int i = 0; i < normals->size(); i++)
    {
        if (pcl::isFinite<pcl::Normal>((*normals)[i]))
        {
            // PCL_WARN("normals[%d] is finite\n", i);
            continue;
        }
        cloudNan->push_back(cloud->points[i]);
        normalsNan->push_back(normals->points[i]);
    }
    cloudNan->points.resize (cloudNan->width * cloudNan->height);
    normalsNan->points.resize (normalsNan->width * normalsNan->height);
    cout<<"size:"<<cloudNan->size()<<endl;

    pcl::VFHEstimation<PointXYZ,Normal,VFHSignature308> VFH;
    VFH.setInputCloud(cloud);
    VFH.setInputNormals(normals);
    VFH.setRadiusSearch(0.03);
     pcl::search::KdTree<pcl::PointXYZ>::Ptr VFHtree(new pcl::search::KdTree<pcl::PointXYZ>());
    VFH.setSearchMethod(tree);
    VFH.compute(*cloudVFH);
    cout<<"size:"<<cloudVFH->size()<<endl;
    
    plotter->setXRange(0, 350); //设置y轴范围
    double x[308];
    double y[308];
    
    for(int i=0;i<308;i++)
    {
        x[i]=i;
        y[i]=(cloudVFH->points[0].histogram[i]);
    }
  while (!plotter->wasStopped())
  {

    plotter->addPlotData (x, y, 308, "VFH");//x,y,点的个数，曲线名
    plotter->spinOnce(2000);
    plotter->clearPlots();
  }    
    return 0;
}