CV攻城狮入门VIT(vision transformer)之旅——近年超火的Transformer你再不了解就晚了!
作者简介:秃头小苏,致力于用最通俗的语言描述问题
专栏推荐:深度学习网络原理与实战
近期目标:写好专栏的每一篇文章
支持小苏:点赞、收藏⭐、留言
文章目录
- CV攻城狮入门VIT(vision transformer)之旅——近年超火的Transformer你再不了解就晚了!
-
- 写在前面
- 整体框架
- self Attention✨✨✨
-
- 执行步骤
-
- step1:获取 q i 、 k i 、 v i q^i、k^i、v^i qi、ki、vi
- step2:计算attention score
- step3:通过softmax层
- step4:得到输出 b i b^i bi
- 代码演示
-
- step1:准备输入
- step2:初始化权重矩阵
- step3:生成 Q 、 K 、 V Q、K、V Q、K、V
- step4:计算attention score
- step5:attn_score矩阵通过softmax层
- step6:将attn_scores_softmax与矩阵V相乘
- 特别注意
- 小结
- Multi-Head Attention✨✨✨
-
- step1:获取 q i 、 k i 、 v i q^i、k^i、v^i qi、ki、vi
- step2:分裂产生多个 q i , j 、 k i , j 、 v i , j q^{i,j}、k^{i,j}、v^{i,j} qi,j、ki,j、vi,j
- step3:对所有head使用self Attention
- step4:拼接所有head输出的结果
- step5:Concat后的结果乘上 W o W^o Wo矩阵
- 小结
- encoder
- decoder
-
- 训练阶段
- 测试阶段
- 总结
- 论文下载地址
- 参考连接
- 附录
-
- input输入解析
-
- Input Embedding
- Positional Encoding(位置编码)
- 小结
CV攻城狮入门VIT(vision transformer)之旅——近年超火的Transformer你再不了解就晚了!
写在前面
近年来,VIT模型真是屠戮各项榜单啊,就像是15年的resnet,不管是物体分类,目标检测还是语义分割的榜单前几名基本都是用VIT实现的!!!朋友,相信你点进来了也是了解了VIT的强大,想一睹VIT的风采。正如我的标题所说,作为一名CV程序员,没有接触过NLP(自然语言处理)的内容,这给理解VIT带来了一定的难度,但是为了紧跟时代潮流,我们还是得硬着头皮往transformer的浪潮里冲一冲。那么这里我准备做一个VIT的入门系列,打算一共分为三篇来讲述,计划如下:
- 第一篇:介绍NLP领域的transformer,这是我们入门VIT的必经之路,我认为这也是最艰难的一步。当然我会尽可能从一个CV程序员的角度来帮助大家理解,也会秉持我写文章的宗旨——通俗易懂,相信你耐心看完会有所收获。
- 第二篇:介绍VIT,即transformer模型在视觉领域的应用,当你对第一篇transformer了解透彻后,这部分难度不大,所谓先苦
后甜,所以大家还是要多花些功夫在第一篇文章理解上。 - 第三篇:梳理VIT的代码,让大家对VIT有一个更加清晰的认识。大家遇到代码也不要有畏难情绪,对于不明白的地方我们大可以
调试看看输出的变化或者查阅文档,总之方法总比困难多!
那么下面我们就要开始了,给大家详细的唠唠transformer!!!准备发车
整体框架
在介绍transformer的整体框架之前,我先来简单说说我们为什么采用transformer结构,即transformer结构有什么优势呢?在NLP中,在transformer出现之前,主流的框架是RNN和LSTM,但这些框架都有一个共同的缺陷,就是程序难以并行化。举个例子,我们期望用RNN来进行语言的翻译任务,即输入I Love China,输出我爱中国。对于RNN来说,要是现在我们要输出中国,就必须先输出我和爱,这个过程是难以并行的,即我们必须先得到一些东西才能进行下一步。【注:这里不知大家能否听懂哈,但只要知道传统架构有难以并行化的缺陷即可】
这样的话,就可以顺理成章的提出transformer了,其最主要就是解决了类似RNN框架难以并行的特点。后文我也会详细介绍transformer是如何进行并行处理数据的。
现在就让我们来看看transformer的整体框架,如下图所示:【注:下图图片公式皆为论文中所截,这里整理到了一起】
看了上图,不用想太多,你就是不理解,我想任谁第一眼看到这堆玩意都是懵逼的,但是没关系,后面我会慢慢的解析这个图。
这一部分我想大致介绍一下这篇文章的行文安排,这样大家应该就不会有很乱的感觉。首先我会介绍self Attention模块和Multi-Head Attention模块。这两部分是transformer的核心,可以这么说,搞懂了这两个部分transformer你基本就掌握大部分了。接着我会讲解encoder和decoderr模块,明白的Multi-Head Attention后,其实encoder和decoder模块就非常简单了。最后,我会做一个总结,提出我的一些思考和看法。
self Attention✨✨✨
在写这部分之前呢,我觉得有必要提醒一下大家,对于我下面讲述的内容你可能会很难理解self Attention为什么会这么做,我给的意见是大家先不用过多的在意,而是先了解self Attention的过程,这个过程理解后,你可能就会对self Attention产生自己独特的认识,当然这部分介绍完后我也会给出自己的理解供大家参考。此外,这部分我会先给出self Attention的执行步骤,然后会结合代码帮大家更深入的理解这个过程,大家务必耐心看完!!!
【注:执行步骤部分的图都为自己所画,一方面希望能用自己的思路表述清楚这部分,另一方面也想在锻炼一下自己的作图水平,作图不易,恳请大家点赞支持,转载请附链接。代码演示部分参考这篇文章】
执行步骤
step1:获取 q i 、 k i 、 v i q^i、k^i、v^i qi、ki、vi
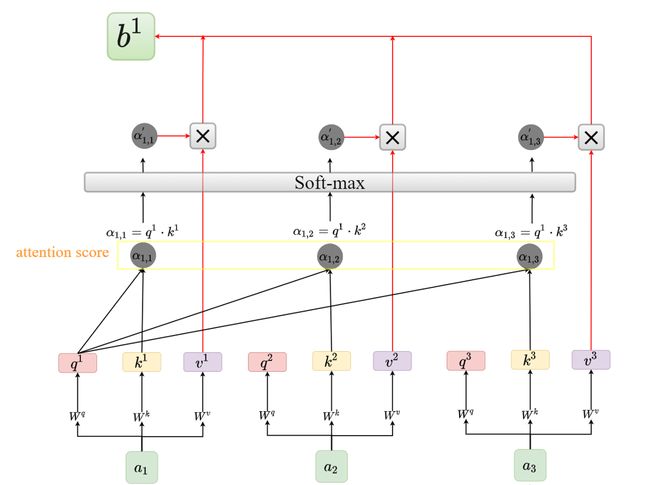
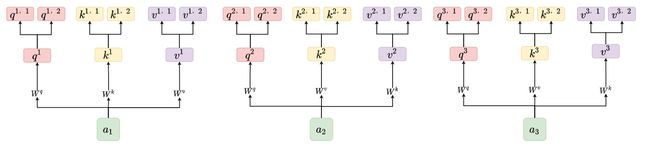
下面我就来介绍self Attention的步骤了。首先,需要有一系列的输入,以三个输入 a 1 a_1 a1、 a 2 a_2 a2、 a 3 a_3 a3 为例,我们分别将 a 1 a_1 a1、 a 2 a_2 a2、 a 3 a_3 a3 乘以 W q W_q Wq、 W k W_k Wk、 W v W_v Wv 矩阵得到对应的 q q q、 k k k、 v v v ,如下图所示:
需要注意的是这里的 W q W_q Wq、 W k W_k Wk、 W v W_v Wv 是共享的。【注:或许你还不明白 a 1 a_1 a1、 a 2 a_2 a2、 a 3 a_3 a3 怎么通过乘一个矩阵变成 q q q、 k k k、 v v v 的,不用担心,在执行步骤介绍完后,我会举一些特例结合代码帮大家理解这些过程,所以还是像我先前说到那样对不理解的点先不用着急,耐心的看完你可能会有所收获!!!】
在每给出一个执行步骤后,我都会列出这部分执行的图解公式,其实这些都是一些矩阵运算,如下图所示:
step2:计算attention score
得到这些 q q q、 k k k、 v v v 后,我们会分别用q去乘每一个 k T k^T kT得到一个数值 a i j a_{ij} aij,即用 q 1 分 别 乘 k 1 T 、 k 2 T 、 k 3 T q_1分别乘k_1^T、k_2^T、k_3^T q1分别乘k1T、k2T、k3T; q 2 分 别 乘 k 1 T 、 k 2 T 、 k 3 T q_2分别乘k_1^T、k_2^T、k_3^T q2分别乘k1T、k2T、k3T; q 3 分 别 乘 k 1 T 、 k 2 T 、 k 3 T q_3分别乘k_1^T、k_2^T、k_3^T q3分别乘k1T、k2T、k3T,如下图所示:【注:为方便表示,先使用 q 1 分 别 乘 k 1 T 、 k 2 T 、 k 3 T q_1分别乘k_1^T、k_2^T、k_3^T q1分别乘k1T、k2T、k3T得到 a 1 , 1 、 a 1 , 2 、 a 1 , 3 a_{1,1}、a_{1,2}、a_{1,3} a1,1、a1,2、a1,3】
a 1 , 1 、 a 1 , 2 、 a 1 , 3 a_{1,1}、a_{1,2}、a_{1,3} a1,1、a1,2、a1,3是一个数值,我们称为attention score,其表示的是每个输入的重要程度。这部分的图解公式如下:
step3:通过softmax层
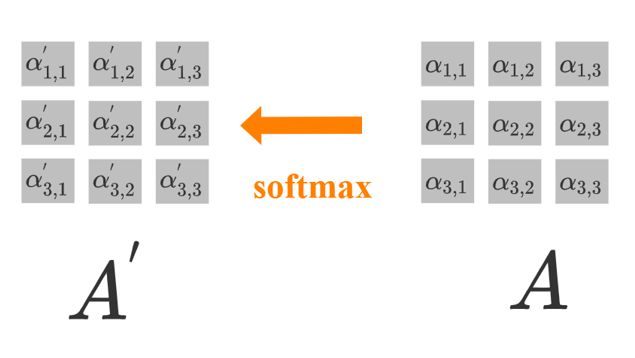
这步就比较简单了,即把上步得到的 a 1 , 1 、 a 1 , 2 、 a 1 , 3 a_{1,1}、a_{1,2}、a_{1,3} a1,1、a1,2、a1,3经过一个softmax层得到输出 a 1 , 1 ′ 、 a 1 , 2 ′ 、 a 1 , 3 ′ a_{1,1}^{'}、a_{1,2}^{'}、a_{1,3}^{'} a1,1′、a1,2′、a1,3′,如下图所示:
这里有一点我需要说明,如果你看attention的论文或者一些文章解读,在经过softmax层前会除了一个 d k \sqrt {{{\rm{d}}_k}} dk,起到了一个归一化的作用,我这里没有除, 因为后面代码举例时不除这个 d k \sqrt {{{\rm{d}}_k}} dk会更方便大家理解,至于这里除不除 d k \sqrt {{{\rm{d}}_k}} dk对大家理解是没有任何影响的,而且不除 d k \sqrt {{{\rm{d}}_k}} dk其实也是一种方法。
这里在给出此步骤的图解公式:
step4:得到输出 b i b^i bi
得到 a 1 , 1 ′ 、 a 1 , 2 ′ 、 a 1 , 3 ′ a_{1,1}^{'}、a_{1,2}^{'}、a_{1,3}^{'} a1,1′、a1,2′、a1,3′后,会让其分别乘 v 1 、 v 2 、 v 3 v_1、v_2、v_3 v1、v2、v3 再相加得到 b 1 b^1 b1,过程如下:
这部分的图解公式如下:
上文通过 q 1 分 别 乘 k 1 T 、 k 2 T 、 k 3 T q_1分别乘k_1^T、k_2^T、k_3^T q1分别乘k1T、k2T、k3T最终得到 b 1 b^1 b1 ,同理我们可以通过 q 2 分 别 乘 k 1 T 、 k 2 T 、 k 3 T q_2分别乘k_1^T、k_2^T、k_3^T q2分别乘k1T、k2T、k3T和 q 3 分 别 乘 k 1 T 、 k 2 T 、 k 3 T q_3分别乘k_1^T、k_2^T、k_3^T q3分别乘k1T、k2T、k3T得到 b 2 和 b 3 b^2和b^3 b2和b3。如下图所示:
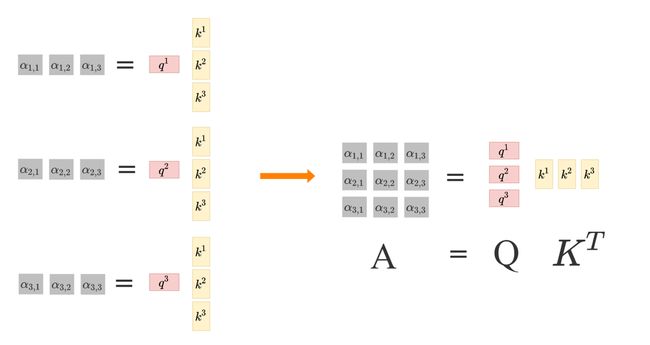
在上述step2、step3和step4中,由于没有介绍 b 2 和 b 3 b^2和b^3 b2和b3的生成过程,因此只给出了有关 b 1 b^1 b1的图解公式。这里再补充上完整的图解公式,如下:
step2:
step3:
step4:
最后,为让大家理解此过程是并行的,我将步骤1到步骤4的过程整合在一起,其中 I I I表示输入的向量,通过下图可以很明显的看出这些矩阵运算是可以并行的,即我们把所有的输入 a i a_{i} ai拼在一起成为 I I I,将I输入网络进行一系列的矩阵运算。
代码演示
这部分会根据上述的理论过程结合代码加深各位的理解。此外,这部分我也会分步骤介绍,但会细化理论部分的步骤,这样大家理解起来会更舒服,但整体的步骤是没有变的。
step1:准备输入
我们定义的输入有三个,它们的维度都是1×4的,将它们放在一起构成一个3×4的输入张量,代码如下:
import torch
x = [
[1, 0, 1, 0], # Input 1
[0, 2, 0, 2], # Input 2
[1, 1, 1, 1] # Input 3
]
x = torch.tensor(x, dtype=torch.float32)
我们来看看输入x的结果:
## 输出结果
tensor([[1., 0., 1., 0.],
[0., 2., 0., 2.],
[1., 1., 1., 1.]])
step2:初始化权重矩阵
我们知道要拿输入x和权重矩阵 W q W_q Wq、 W k W_k Wk、 W v W_v Wv分别相乘得到 q q q、 k k k、 v v v,而x的维度是3×4,为保证矩阵可乘,可设 W q W_q Wq、 W k W_k Wk、 W v W_v Wv的维度都为4×3,这样得到的 q q q、 k k k、 v v v都为3×3维。
w_query = [
[1, 0, 1],
[1, 0, 0],
[0, 0, 1],
[0, 1, 1]
]
w_key = [
[0, 0, 1],
[1, 1, 0],
[0, 1, 0],
[1, 1, 0]
]
w_value = [
[0, 2, 0],
[0, 3, 0],
[1, 0, 3],
[1, 1, 0]
]
##将w_query、w_key、w_value变成张量形式
w_query = torch.tensor(w_query, dtype=torch.float32)
w_key = torch.tensor(w_key, dtype=torch.float32)
w_value = torch.tensor(w_value, dtype=torch.float32)
step3:生成 Q 、 K 、 V Q、K、V Q、K、V
这步就是矩阵的乘法,注意@表示矩阵的乘法,*表示矩阵按位相乘。代码如下:
querys = x @ w_query
keys = x @ w_key
values = x @ w_value
同样的,我们可以看看此步得到的 Q 、 K 、 V Q、K、V Q、K、V结果:
## Q
tensor([[1., 0., 2.],
[2., 2., 2.],
[2., 1., 3.]])
## K
tensor([[0., 1., 1.],
[4., 4., 0.],
[2., 3., 1.]])
## V
tensor([[1., 2., 3.],
[2., 8., 0.],
[2., 6., 3.]])
step4:计算attention score
计算attention score其实就是计算 Q ⋅ K T Q \cdot K^T Q⋅KT ,代码如下:
attn_scores = querys @ keys.T
计算得到的attn_scores结果如下:
##attn_scores
tensor([[ 2., 4., 4.],
[ 4., 16., 12.],
[ 4., 12., 10.]])
注意,上图只画出了 q 1 ⋅ K T q_1 \cdot K^T q1⋅KT的计算结果,为 [ 2. , 4. , 4. ] [2., 4., 4.] [2.,4.,4.] ,同理你可以得到 q 2 ⋅ K T q_2 \cdot K^T q2⋅KT 和 q 1 ⋅ K T q_1 \cdot K^T q1⋅KT的结果,分别为 [ 4. , 16. , 12. ] [4., 16., 12.] [4.,16.,12.] 和 [ 4. , 12. , 10. ] [4., 12., 10.] [4.,12.,10.] ,将它们组合在一起即得到了attn_scores矩阵,其维度为3×3。
step5:attn_score矩阵通过softmax层
将上步得到的attn_scores输入softmax层,代码如下:
from torch.nn.functional import softmax
attn_scores_softmax = softmax(attn_scores, dim=-1)
我们可以来看看attn_scores_softmax的结果:
tensor([[6.3379e-02, 4.6831e-01, 4.6831e-01],
[6.0337e-06, 9.8201e-01, 1.7986e-02],
[2.9539e-04, 8.8054e-01, 1.1917e-01]])
上面的结果有效数字太多了,后文不好教学展示,因此我们对attn_scores_softmax的结果取小数点后一位,即attn_scores_softmax变成下列形式:
attn_scores_softmax = [
[0.0, 0.5, 0.5],
[0.0, 1.0, 0.0],
[0.0, 0.9, 0.1]
]
##转换为tensor格式
attn_scores_softmax = torch.tensor(attn_scores_softmax)
##输出attn_scores_softmax结果
#tensor([[0.0000, 0.5000, 0.5000],
# [0.0000, 1.0000, 0.0000],
# [0.0000, 0.9000, 0.1000]])
step6:将attn_scores_softmax与矩阵V相乘
这部分代码如下:
outputs = attn_scores_softmax@values
这里可以看一下这部分的输出:
# outputs结果
tensor([[2.0000, 7.0000, 1.5000],
[2.0000, 8.0000, 0.0000],
[2.0000, 7.8000, 0.3000]])
注意:这部分不是按照参考链接所给代码写的,参考链接中把这步拆分成了两个部分,还涉及到了三维矩阵的乘法,我认为是不好理解的,感兴趣的可以自己去看看。
特别注意
代码演示这部分的代码和图是参考Illustrated: Self-Attention 这篇文章,我觉得写的非常好,图文并茂的展现了self Attention的过程。但是我认为这个例子似乎是有一些缺陷的,当然了,这里所说的缺陷并没有针对作者对self Ateention的解释,而是这个例子不能对应我们下文提出的encoder和decoder模块,我现在说encoder 和decoder 模块你肯定还不明白说的是什么,但是我这里先提出这个例子的缺陷,大家有个印象就好。
那到底是什么缺陷呢?我们可以直接来看上文step7中图片,可以发现我们输入的是3个4维向量,即维度为3×4;而输出为3个三维向量,即维度为3×3。这里的维度是不同的,这主要是由于我们在由输入生成 Q 、 K 、 V Q、K、V Q、K、V时所乘的权重矩阵 W q W_q Wq、 W k W_k Wk、 W v W_v Wv维度导致的。那么输入输出的维度不一致为什么会在encoder 和 decoder 出现问题呢?其实啊,在Attention操作后都会接上一个残差模块,这就要求Attention 操作前后输入输出的维度一致。
讲到这里,我相信大家已经知道问题就出在输入输出的维度上的,那么后文我们就会默认经过Attention模块后输入输出的维度保持不变。
这部分我没有修改这部分代码及图片一方面是偷了个懒,另一方面是想让大家更加深刻的意识到这个输入输出维度的问题。还有一点需要注意,在下文介绍Multi-Head Attention时是最后通过乘一个 W o W^o Wo矩阵实现的,在相关部分我也会介绍。
小结
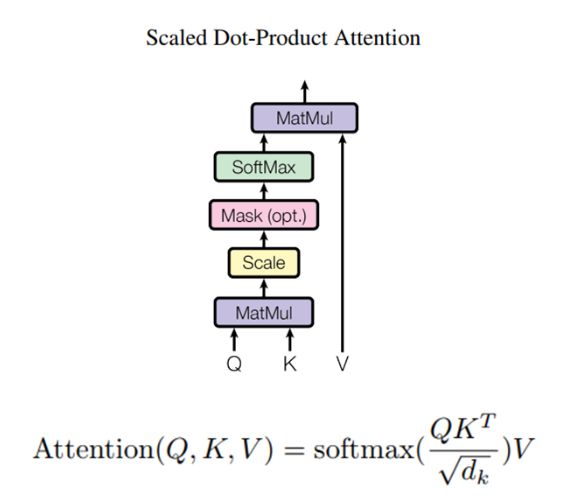
最后我们来对照整体框架的第一张图来看看self Attention的过程,如下图:
对于上图其实有两点和我们上文讲述的有所差异,第一点是红色底框中的Mask是可选的(opt.),我们并没有采用,关于这个Mask我会在后文讲述decoder模块部分进行讲解;还有一点是上图采用的是Scaled Dot-Product Attention,而我们采用的是Dot-Product Attention,这两个有什么区别呢?其实区别我们在step3:通过softmax层有提到,即没有除以 d k \sqrt {{{\rm{d}}_k}} dk。
到这里,self Attention的内容就介绍完了。我自认为讲解得算是比较清楚的了,希望能对大家有所帮助。
Multi-Head Attention✨✨✨
Multi-Head Attention称为多头注意力机制,其实你理解了上文的自注意力机制(self Attention),再来看这部分其实就很简单了,下面就跟着我一起来学学吧!!!
step1:获取 q i 、 k i 、 v i q^i、k^i、v^i qi、ki、vi
首先第一步和self Attention一模一样,获取 q i 、 k i 、 v i q^i、k^i、v^i qi、ki、vi,如下图所示:
step2:分裂产生多个 q i , j 、 k i , j 、 v i , j q^{i,j}、k^{i,j}、v^{i,j} qi,j、ki,j、vi,j
以下以两个head为例进行阐述,即将 q 1 q^1 q1分裂成两个 q 1 , 1 和 q 1 , 2 q^{1,1}和q^{1,2} q1,1和q1,2,将 q 2 q^2 q2分裂成两个 q 2 , 1 和 q 2 , 2 q^{2,1}和q^{2,2} q2,1和q2,2,将 q 3 q^3 q3分裂成两个 q 3 , 1 和 q 3 , 2 q^{3,1}和q^{3,2} q3,1和q3,2如下图所示:
那么这个过程是怎么进行的呢,其实也很简单,只需要分别乘上两个矩阵 W 1 Q W_1^Q W1Q和 W 2 Q W_2^Q W2Q即可。【注意: q 1 、 q 2 、 q 3 乘 q_1、q_2、q_3乘 q1、q2、q3乘 W 1 Q W_1^Q W1Q会分别得到 q 1 , 1 、 q 2 , 1 、 q 3 , 1 q^{1,1}、q^{2,1}、q^{3,1} q1,1、q2,1、q3,1; q 1 、 q 2 、 q 3 乘 q_1、q_2、q_3乘 q1、q2、q3乘 W 2 Q W_2^Q W2Q会分别得到 q 1 , 2 、 q 2 , 2 、 q 3 , 2 q^{1,2}、q^{2,2}、q^{3,2} q1,2、q2,2、q3,2】
为了方便大家理解,结合特例作图如下:即我们只需有 W 1 Q W_1^Q W1Q和 W 2 Q W_2^Q W2Q矩阵即可将 q q q分成多个。
同理,我们可以将 k 和 v k和v k和v采用同样的方法,即都相应的乘以两个矩阵进行分裂,结果如下图所示:
step3:对所有head使用self Attention
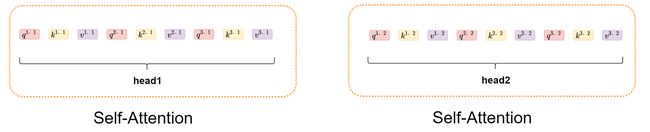
我们可以将上述结果分成两个head进行处理,如下图所示:
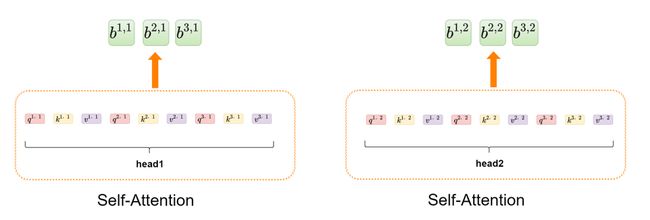
你会发现head1和head2就是我们前面所说的self Attention里面的元素,这样会从head1和head2得到对应输出,如下图所示:
step4:拼接所有head输出的结果
这一步我们会将上一步不同head输出的结果进行Concat拼接,如下图所示:
step5:Concat后的结果乘上 W o W^o Wo矩阵
这一步会乘上 W o W^o Wo矩阵,其作用主要是融合之前多个head的结果,并使我们的输出和输入时维度保持一致,如下图所示:【注:这里是不是和我们介绍Self Attention模块时讲的特别注意部分很像呢,即Multi-Head Attention是通过 W o W^o Wo矩阵控制输入输出维度一致的】
小结
同样的,这里我们也来对照整体框架中的图片来看看Multi-Head Attenton的过程,如下图所示:
你会发现这副图画的比较抽象,用虚影表示出多个head的情景,我想大家是能够理解的。需要注意的一点是上图中的Linear操作其实就是指我们对原数据乘一个矩阵进行变换。
那么到这里,Multi-Head Attention的内容就介绍完了,希望能对大家有所帮助。
encoder
encoder模块结构如下图黄色虚线框内所示:
首先我们要先介绍一下输入,即上图Input Embedding + Positional Encoding 部分,因为这部分我认为内容还是挺多的,因此放在了附录部分,大家可先点击查看。
了解了输入,其实就剩下了灰色框部分,其实这部分还蛮简单的,其主要由两个小部分组成,其一是Multi-Head Attention+Add&Norm,其二是Feed Forward+Add&Norm。
我们先来介绍第一小部分,假设输入是维度为(N,d)的矩阵,用 I I I 来表示,首先会进入一个Multi-Head Attention模块,这部分我们上文已经详细介绍过了,这里不再阐述,通过Multi-Head Attention模块后得到输出 B B B ,其维度同样是(N,d)。接着使用一个残差模块将 I I I 和 B B B 加到一起得到 B ‘ , 最 后 对 B ‘ {{\rm{B}}^`} , 最后对{{\rm{B}}^`} B‘,最后对B‘ 进行Layer Normalization操作得到输出 O 1 O_1 O1,其维度同样是(N,d)。【关于Layer Normalization不了解的可以参考我的这篇文章:Batch_Normalization 、Layer_Normalization 、Group_Normalization你分的清楚吗 】
这部分操作的表达式如下:
O 1 = L a y e r N o r m a l i z a t i o n ( I + M u l t i - H e a d A t t e n t i o n ( I ) ) O_1=Layer \ Normalization(I + Multi\text{-}Head Attention(I)) O1=Layer Normalization(I+Multi-HeadAttention(I))
是不是发现这种表达式一下子就把上图的结构都展现出来了呢,所以数学真的很奇妙!!!
接下来来介绍第二小部分。这回的输入即为 O 1 O_1 O1,维度为(N,d)。首先会进入一个Feed Forward网络,这是什么呢,其实很简单,就是两个全连接层,如下图所示:
经过Feed Forward层后,我们的输出为 O 1 1 O_1^1 O11,前后尺寸保持不变。接着我们同样会进行Add和Layer Normalization操作,最后得到输出 O 2 O_2 O2,此时 O 2 O_2 O2的维度同样为(N,d)。
这部分操作的表达式如下:
O 2 = L a y e r N o m a l i z a t i o n ( O 1 + F e e d F o r w a r d N e t w o r k ( O 1 ) ) O_2=Layer \ Nomalization(O_1+Feed \ Forward \ Network(O_1)) O2=Layer Nomalization(O1+Feed Forward Network(O1))
这样我们就算是把一个encoder网络介绍完了,细心的同学可能会发现encoder结构图傍边写了个 N × N× N×,没错啦,和大家想的一样,我们会将这个结构重复N次。重复N次就不要我讲了叭,但需要强调一点,一个网络结构要能够重复堆叠,那么它的输入输出的维度应该是一致的,很显然我们上面介绍的结构满足这已条件。
这部分是不是发现还蛮简单滴,同样,希望大家都有所收获!!!
decoder
decoder的结构如下图黄色虚线框内所示:
decoder的结构相较于encoder就难多了,一共包含四个子结构(灰色框中三个),分别为Masked Multi-head Attention+Add&Norm 、Multi-Head Attention+Add&Norm 、 Feed Forward+Add&Norm 和 Linear+Softmax。
我觉得这部分最难理解的就是训练和测试是不同的,下面我将分为训练阶段和测试阶段来为大家讲解这个decoder模块。
训练阶段
我们先来讲讲decoder的训练阶段是如何运行的。首先要明确我们的任务——将“我有一只猫”翻译成“I have a cat”。选用这个例子也是我看网上资料基本都是这个例子,图片都是于此相关的,这部分我实在是不想再画图了,这篇文章确实写的太久了,也太累了,所以也就偷个懒,就借用一下别人的图啦!!!【这里的参考链接我放在最后那部分,因为我看评论区博主说这些图片是一篇英文博客上的,不过我没找到原始博客】
接着我们来看看decoder的输入和输出是什么:
- 输入:encoder的输出和decoder自身的输出
- 输出:输出词的概率分布
对于这个输入输出你现在可能还不是很理解,接下来我会慢慢分析。
我觉得很有必要的一点是让大家清楚decoder结构主要做了什么?——decoder会根据之前的翻译,求得目前最有可能的翻译结果。例如输入“
这里不知道大家能否明白,我当时看这部分时还是有所困惑的,即我们的任务不是将“我有一只猫”翻译成“I have a cat”嘛,为什么这里输入和输出都是英文啊?这块我没看到相关的解释,可能时我们CV程序员对NLP的理解有所欠缺,我谈谈自己的看法——我认为大家和我进入了一个误区,即decoder的输入到底是什么?通过我上文的我们可以知道decoder输入为encoder的输出和decoder自身的输出。可以看到,decoder根本就没有把“我是一只猫”作为输入,它会先输入一个开始标志
如果大家觉得自己明白了这一部分,先给自己点个赞!!!然后我再来问大家一个问题看看你是否是真的明白了呢——为什么我们输入
傻瓜!!!这当然是我们训练的结果啦!!!不然这傻瓜机器怎么会这么智能。我简单的画个图为大家解释解释。

上图展示了我们训练的大致过程,即我们输入
这回大家是不是对Decoder的理解更近一步了呢?如果是的话,我就再来问大家一个问题——我们输入
到这里,我相信大家对decoder整体的训练已经有了一个较清晰的认识。下面我就来结合decoder的结构图来看看decoder里到底都有些什么。
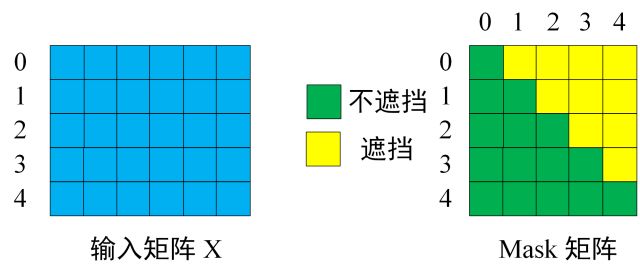
首先是输入部分,这部分我在上文中讲述的已经够清楚了。在训练阶段我们会将“0 1 2 3 4分别代表“
-
得到输入矩阵和Mask矩阵,两者维度一致。图中显示遮挡位置的值为0。可以发现单词0只能使用单词0的信息,单词1可以使用单词0和单词1的信息。
-
通过输入矩阵X计算得到 Q 、 K 、 V Q、K、V Q、K、V并计算 Q ⋅ K T Q \cdot K^T Q⋅KT
-
Q ⋅ K T Q \cdot K^T Q⋅KT 与Mask矩阵按位相乘,得到 M a s k Q ⋅ K T Mask \ \ Q \cdot K^T Mask Q⋅KT
-
对 M a s k Q ⋅ K T Mask \ \ Q \cdot K^T Mask Q⋅KT 进行Softmax操作,使 M a s k Q ⋅ K T Mask \ \ Q \cdot K^T Mask Q⋅KT矩阵的每一行相加都为1
-
M a s k Q ⋅ K T Mask \ \ Q \cdot K^T Mask Q⋅KT与矩阵V相乘,得到输出Z
上述过程只展示的是一个Head的情况,输出了Z,最后应该把所有Head的结果拼接,使最终的Z和输入X的维度一致。
Masked Multi-Head Attention结束后使一个Add&LayerNormalization层,这个我在encoder中已经讲述的很清楚了,这里不再赘述。经过Add&LayerNormalization层后的输出维度仍和输入X维度一致。
接着会进入第二个Multi-Head Attention层,注意此时的 K 、 V K、V K、V来自于encoder,而 Q Q Q来自decoder。这样做的好处是在decoder时,每一个词都可以利用encoder中所有单词的信息。接着同样是一个Add&LayerNormalization层。
然后会进入Feed Forward+Add&Norm层,接着会将整个结构重复N次。
最后会进入Linear+Softmax层,最终输出预测的单词,因为 Mask 的存在,使得单词 0 的输出 Z(0,) 只包含单词 0 的信息,如下:
Softmax 根据输出矩阵的每一行预测下一个单词,如下图所示:
这部分我推荐大家听听李宏毅老师的课程:台大李宏毅21年机器学习课程 self-attention和transformer
测试阶段
明白了上文训练阶段decoder是怎么工作的,那么测试阶段就很容易理解了。其实我在训练阶段也有提及,主要区别就是此时我们不是一次将“
- 输入
,decoder输出 I 。 - 输入前面已经解码的
和 I,decoder输出have。 - 输入已经解码的“
I have a cat”,decoder输出解码结束标志位,每次解码都会利用前面已经解码输出的所有单词嵌入信息。
那么很明显测试阶段我们是无法做并行化处理的!!!
总结
终于算是把transformer的内容讲完了,这里我给出一张Transformer的整体结构图,我觉得画的非常好,如下图所示:【图片来源于此篇文章】
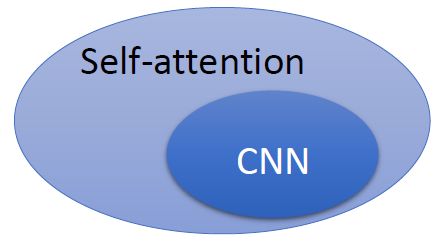
另外,作为CV程序员的我们,往往对CNN网络是更加熟悉的。那么CNN和Transformer中的self-Attention是否有什么联系呢?大家可以去网上找找资料,其实CNN可以看作是一种简化版的self-Attention,或者说self-Attention是一种复杂化的CNN,它们的大致关系如下:
我们知道越复杂的模型,往往就需要更多的参数来训练,因此在训练Transformer时就需要更多的数据,关于这一点在后面讲述的VIT模型中会有体现,敬请期待吧!!!
最后的最后,还是希望大家有所收获!!!另外,如果文章对你有所帮助,希望得到你小小的赞,这是对创作最大的支持
论文下载地址
Attention Is All You Need
参考连接
1、Transformer中Self-Attention以及Multi-Head Attention详解
2、台大李宏毅21年机器学习课程 self-attention和transformer
3、Transformer论文逐段精读【论文精读】
4、ViT论文逐段精读【论文精读】
5、shusheng wang 讲解 Transformer模型
6、Illustrated: Self-Attention
7、Vision Transformer 超详细解读 (原理分析+代码解读) (一)
8、Transformer Decoder详解
9、Transformer模型详解(图解最完整版)
附录
input输入解析
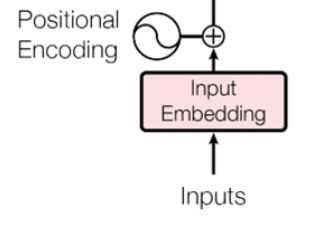
这部分来谈谈encoderr的输入部分,其结构示意图如下:
上图主要包含两个概念,一个是Input Embedding ,一个是Positional Encoding。下面就来逐一的进行介绍。
Input Embedding
我们先来看Input Embedding,何为Input Embedding呢?这里我先卖个关子,先不介绍这个概念,而是先从我们的输入一点点谈起。现假设我们要实现一个文本翻译任务,假设具体任务为将汉字“秃 头 小 苏 ”翻译成拼音“tu tou xiao su”,这里我们只关注输入,此时的输入应该是“秃 头 小 苏”四个汉字,但是作为程序猿的我们应该知道,这四个汉字计算机是不认识的,那么就需要将“秃 头 小 苏”转化为计算机认识的语言,一种常见的做法是独热编码(one-hot编码),如下图所示:【对于独热编码不熟悉的自行百度,这里不再介绍】

可以看出,上图可以用一串数字表示出“秃 头 小 苏”这四个汉字,如用1 0 0 0表示“秃”,用0 1 0 0表示“头”…
但是这种表示方法是否存在缺陷呢?大家都可以思考思考,我给出两点如下:
- 这种编码方式对于我这个案例来说貌似是还蛮不错的,但是大家有没有想过,对于一个文本翻译任务来说,往往里面有大量大量的汉字,假设有10000个,那么一个单独的字,如“秃”就需要一个1×10000维的矩阵来表示,而且矩阵中有9999个0,这无疑是对空间的一种浪费。
- 这种编码方式无法表示两个相关单词的关系,如“秃”和“头”这两个单词明显是有某种内在的关系的,但是独热编码却无法表示这种关系。
那么我们采用什么方法来缓解这种问题呢?答案就是Embedding!!!那么何为Embedding呢,我的理解就是改变原来输入input的维度,。比如我们现在分别先用“1”,“2”,“ 3”,“ 4” 分别代表“秃”,“头”,“小”,“苏”这四个字,然后将“1”,“2”,“ 3”,“ 4”送入embedding层,代码如下:
import torch
import torch.nn as nn
embedding = nn.Embedding(5, 3)
input = torch.IntTensor([[1,2,3,4]])
上文代码(5,3)中的3就代表我们输出每个单词的维度,可以看一下输出结果,如下图所示:
输出矩阵的每一行都代表了一个词,如第一行[0.2095 -0.6338 0.5679]代表1,即代表“秃”。
我们可以修改一下Embedding的参数,将(5,3)换成(5,4),如下:
import torch
import torch.nn as nn
embedding = nn.Embedding(5, 4)
input = torch.IntTensor([[1,2,3,4]])
这时我们在来看看输出结果,此时每个词就是一个4维向量:
通过上面代码的演示,不知大家有没有体会到Embedding可以控制输入维度的作用呢。有关Embedding函数的使用请参照pytorch官网对此部分的解读,点击☞☞☞了解详情。
最后我们来大致看看通过Embedding后会达到怎样的效果:

可以看出,“秃”和“头”在某个空间中离的比较近,说明这两个词的相关性较大。即Embedding不仅可以控制我们输入的维度,还可以从较高的维度去考虑一些词,那么会发现一些词之前存在某种关联。
Positional Encoding(位置编码)
首先谈谈我们为什么要采用位置编码,还记得我们前文所说的Attention操作嘛,其采用的是并行化的操作,即会将输入一同输入Attention,这种并行化就会导致在输入是没有是没有顺序的。同样拿输入“秃 头 小 苏”为列,没有加入位置编码时,我们不管时输入“秃 头 小 苏”、“小 头 苏 秃”或其它等等,对我们的输出结果是没有任何影响的,这部分此篇文章还简单的做了个小实验,大家可以参考一下。
通过上文的介绍,我们知道没有位置编码会导致不管我们的输入顺序如何变换,对于最后的结果是没有影响的,这肯定不是我们期望看到的。那我们就给它整个位置编码呗!可是我们应该采用什么方式的位置编码呢?我想大家可以很自然的想到一个,那就是一个词标一个数字就得了呗,如下表所示:
| 词 | 编码 |
|---|---|
| 秃 | 0 |
| 头 | 1 |
| 小 | 2 |
| 苏 | 3 |
这种编码操作简单,但是编码长度是不可控的,即词的个数越多,后面编码词越大,这样的方式其实不是理想的。
那我们还可以使用什么编码方式呢?既然上述所述编码规则是编码长度不可控,那么就可以通过除以词的长度将其控制在0-1的范围内呀,如下表所示:
| 词 | 编码 |
|---|---|
| 秃 | 0 4 = 0.00 \frac{0}{4}=0.00 40=0.00 |
| 头 | 1 4 = 0.25 \frac{1}{4}=0.25 41=0.25 |
| 小 | 2 4 = 0.50 \frac{2}{4}=0.50 42=0.50 |
| 苏 | 3 4 = 0.75 \frac{3}{4}=0.75 43=0.75 |
你或许觉得这种编码方式还是蛮不错的,但是呢这种方式会导致结果的尺寸会随着词的长度变换而不断变换,即上例中我们每个词编码结果的间距是0.25,但是要是我们有100个词,有100个词时,这个间距又会变成多少呢?这种尺度的不统一,对模型的训练是不友好的。
“你一会介绍这个方法,这个方法不行;一会介绍那个方法,那个方法不行。那到底行不行!!!”,~~呜呜,大佬们别喷啊,我这是想让大家看看有哪些思路,况且论文中所给的编码方式也不一定是最好的,大家都可以多想想嘛。那么下面就给各位老大爷带来论文中关于此部分的位置编码方式,公式如下:
P E p o s , 2 i = s i n ( p o s / ( 1000 0 2 i / d m o d e l ) ) PE_{pos,2i}=sin(pos/(10000^{2i/d_{model}})) PEpos,2i=sin(pos/(100002i/dmodel))
P E p o s , 2 i + 1 = c o s ( p o s / ( 1000 0 2 i / d m o d e l ) ) PE_{pos,2i+1}=cos(pos/(10000^{2i/d_{model}})) PEpos,2i+1=cos(pos/(100002i/dmodel))
不知道大家看到这个公式做何感想呢?反正对我来说我是懵的。下面就为大家来介绍介绍。首先来解释一下公式中符号的含义:pos表示词的位置,同样拿“秃 头 小 苏”为例,pos=0表示第一个词“秃”,pos=1表示第二个词“头”。2i和2i+1表示Positional Encoding(位置编码)的维度,这个怎么理解呢,我们知道2i是偶数位,2i+1是奇数位,假设我们现在对“秃”字进行位置编码,那么位置编码向量的第0个位置,即偶数位采用的是 P E p o s , 2 i = s i n ( p o s / ( 1000 0 2 i / d m o d e l ) ) PE_{pos,2i}=sin(pos/(10000^{2i/d_{model}})) PEpos,2i=sin(pos/(100002i/dmodel))这个公式,而位置编码向量的第1个位置,即奇数位采用的公式为 P E p o s , 2 i + 1 = c o s ( p o s / ( 1000 0 2 i / d m o d e l ) ) PE_{pos,2i+1}=cos(pos/(10000^{2i/d_{model}})) PEpos,2i+1=cos(pos/(100002i/dmodel)) 。 d m o d e l d_{model} dmodel表示输入的维度大小,即我们上小节所述的Input Embedding。【注id的取值范围为 [ 0 , . . . , d m o d e / 2 ] [0,...,d_{mode/2}] [0,...,dmode/2]】
知道了这些符号含义,不知道大家是否有所感悟。如果感觉还差一点的话也没关系,我相信我再举两个例子大家就明白了。首先还是“秃 头 小 苏”这个例子,我们先来看看第一个词“秃”的位置编码:【注:设 d m o d e l d_{model} dmodel=512】

再来看看“头”的编码,如下:

我相信通过上面的例子你应该已经对这种方式的位置编码有所了解了,即你知道了如何用这种方式来对某个词进行编码。但是你可能会问,为什么用这个方式来进行位置编码呢?即这种位置编码的优势在哪里呢?这里我为大家呈现3点:
- 每个位置都有唯一的一个位置编码
- 能够适应比训练集里面所有句子更长的句子,假设训练集里面最长的句子是有 100 个单词,突然来了一个长度为101 的句子,则使用公式计算的方法可以计算出第101位的 Embedding。
- 可以让模型很容易的计算出相对位置。【这一点似乎比较难理解,我详细的为大家说说】
第3点说明:
第3点说可以让模型很容易的计算出相对位置,怎么理解呢,其实就是说任意位置的 P E p o s + k PE_{pos+k} PEpos+k都可以被 P E p o s PE_{pos} PEpos和 P E k PE_{k} PEk表示。这时候很多资料就给大家列出了一个谁都知道的三角公式,如下:
s i n ( α + β ) = s i n ( α ) c o s ( β ) + c o s ( α ) s i n ( β ) sin(\alpha + \beta)=sin(\alpha)cos(\beta)+cos(\alpha)sin(\beta) sin(α+β)=sin(α)cos(β)+cos(α)sin(β)
c o s ( α + β ) = c o s ( α ) c o s ( β ) − s i n ( α ) s i n ( β ) cos(\alpha + \beta)=cos(\alpha)cos(\beta)-sin(\alpha)sin(\beta) cos(α+β)=cos(α)cos(β)−sin(α)sin(β)
后面就没有解释了,这可能就是专家视角吧!!!认为谁都知道,可是我却不认为大家都能明白其中的含义,至少我当时就没明白。【大佬请忽略】下面我就为大家解释解释为什么通过这两个三角公式就会使任意位置的 P E p o s + k PE_{pos+k} PEpos+k都可以被 P E p o s PE_{pos} PEpos和 P E k PE_{k} PEk表示,如下图所示:【注:为方便公式书写,这里令 1000 0 2 i / d m o d e l = M {10000^{2i/{d_{model}}}} = M 100002i/dmodel=M】
通过上图可以看出,对于pos+k位置的位置编码可以表示位pos位置和k位置的线性组合。这样的线性组合意味着某个位置向量蕴含了其它位置向量的信息。
【注:可能很多人会问为什么这个M,即 1000 0 2 i / d m o d e l {10000^{2i/{d_{model}}}} 100002i/dmodel中的10000有什么讲究嘛,其实吧,也没必要选用这个10000,之前看过一篇英文文章,就对这个数进行过分析,但是我现在找不着链接了,总之大家不用特别纠结这个10000】
小结
最后,我们再来看看这张图:
可以看出我们最后的输入会将Input Embedding 和Positional Encoding进行相加,那么这就要求Input Embedding 和Positional Encoding的维度使一致的。这里大家会不会有这样的疑问呢,我们将Input Embedding 和Positional Encoding相加,不是会将原来表示位置信息的Positional Encoding混入到Input Embedding中了,这样不就感觉很难再找到Positional Encoding的信息了嘛?似乎采用concat(拼接)更加合适吧!!!这里给出一种解释,参考的是这篇文章:【Positional Encoding用 e i e^i ei表示,Input Embedding 用 a i a^i ai表示】
我们先给每一个位置的 x i ∈ R ( 1 , d ) x^i \in R(1,d) xi∈R(1,d) append一个位置编码的向量 p i ∈ R ( 1 , N ) p^i \in R(1,N) pi∈R(1,N) ,得到一个新的输入向量 p i ∈ R ( 1 , d + N ) p^i \in R(1,d+N) pi∈R(1,d+N),这个向量作为新的输入,乘以一个transformation matrix W = [ W I W p ] ∈ R ( d + N , d ) W=\left[ \begin{array}{cc} {W^I}\\ {{\rm{W}}^p} \end{array} \right] \in R(d+N,d) W=[WIWp]∈R(d+N,d) 。那么:
x p i ⋅ W = [ x i p i ] ⋅ [ W I W p ] = x i ⋅ W I + p i ⋅ W P = a i + e i x_p^i⋅ W =[x^ip^i]⋅\left[ \begin{array}{cc} {W^I}\\ {{\rm{W}}^p} \end{array} \right]=x^i⋅W^I+p^i⋅W^P=a^i+e^i xpi⋅W=[xipi]⋅[WIWp]=xi⋅WI+pi⋅WP=ai+ei
所以, e i e^i ei与 a i a^i ai相加就等同于把原来的输入 x i x^i xiconcat一个表示位置的位置编码 p i p^i pi ,再做transformation。
大家觉得这个解释怎么样呢?我当时看到就觉得这实在是太妙了。那么这部分就为大家呈现这么多了,同样希望大家都收获满满喔!!!
如若文章对你有所帮助,那就
![]()