李宏毅机器学习笔记——误差与梯度下降
误差与梯度下降
- 误差的来源
-
- Variance
- Bias
- 小结
-
- 交叉验证
- 梯度下降
-
- 学习率
-
- 自动调整学习率
- 随机梯度下降
- 特征缩放(Feature Scaling)
- 梯度下降原理
误差的来源
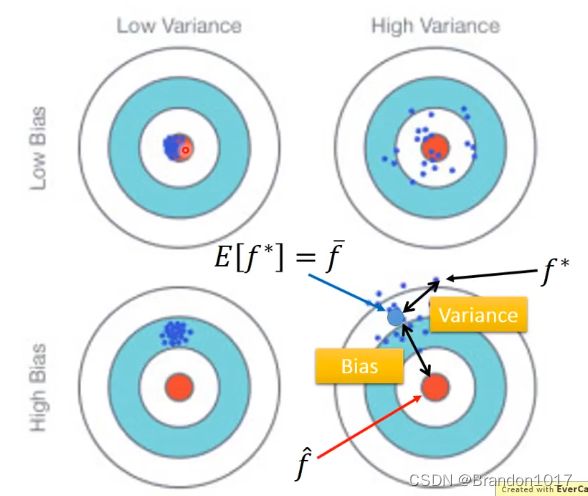
训练得到的模型 f ∗ f^* f∗ 和真实的模型 f ^ \hat f f^ 之间的距离(差距)就是Bias+Variance。
Variance

于是可以得到规律:
简单的模型的Variance比较小,而复杂的模型的Variance比较大。
因为简单的模型受不同的样本的影响比较小,而复杂的模型受样本的影响比较大。
Bias
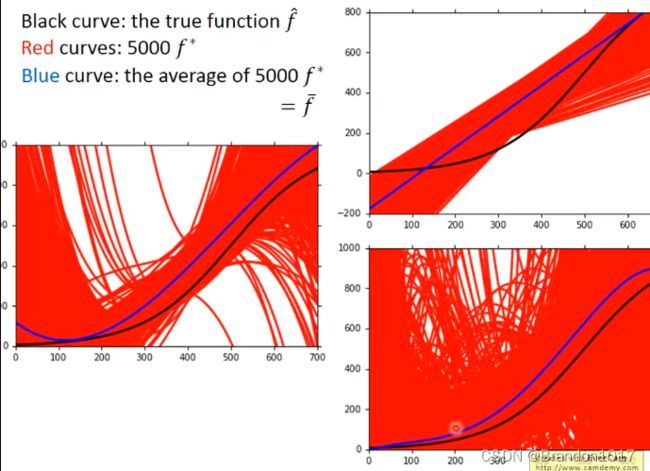
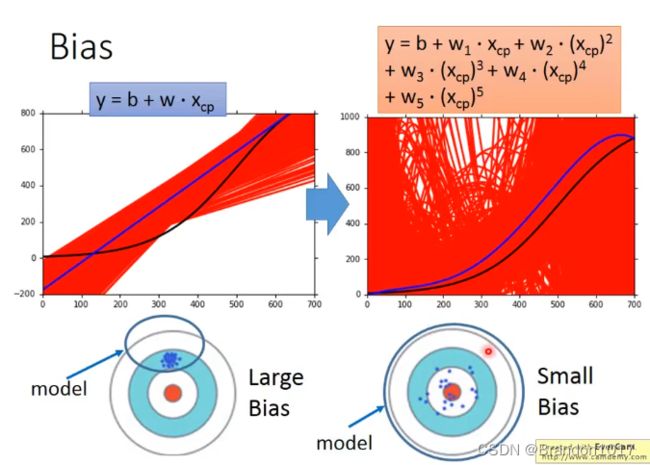
得到规律:
简单的模型的Bias比较大,而复杂的模型的Bias会比较小。
因为简单的模型所在的集合比较小,而复杂的模型所在的集合会比较大,会更可能包含了真实模型,所以会更准确些。
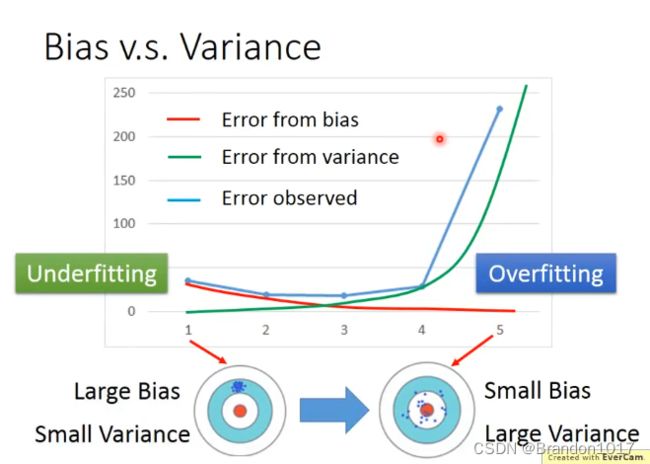
小结
高Bias,低Variance——欠拟合(Underfitting)
诊断:模型在训练集上有较大的误差。
低Bias,高Vairance——过拟合(Overfitting)
诊断:模型在训练集上误差较小,但在测试集上有较大的误差。
对于较大的Bias,我们可以增加特征数或者将模型变得复杂化(加入高次幂或者交互项)。
对于较大的Variance,我们需要更多的训练样本,或者在模型中加入正则项。
交叉验证
于是我们想要得到一个准确的模型,我们需要尽可能地降低Bias和Variance,但我们不能简单地将在测试集上的误差最小的模型作为最终模型,所以我们要将数据集分为:训练集、验证集、测试集。我们把训练好的模型在验证集上选出较优的,然后用测试集进行最终确认。我们不建议将测试集测试的结果反过来再对模型进行改进。
另一种方法:N折交叉验证。
将数据分为训练集和测试集,再将训练集平分为n份,每次将n-1份的数据用作训练,将剩下一份数据作为验证集得到模型误差,这样循环数据可以得到n次的模型误差,再将误差求平均作为这个模型集合训练后的误差,最后比较不同模型集合间的优劣。
梯度下降
回顾:需要找到最优的参数,使得Loss Function最小,我们采用的方法是梯度下降。

学习率
我们要适当选取学习率。
学习率太小,可能更新参数速度太慢。
学习率太大,可能收敛不到最小值。
可以将参数迭代更新的次数和Loss可视化:
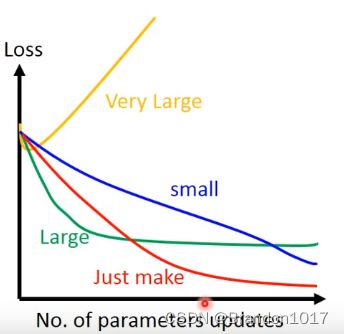
合适的学习率会使得Loss随着迭代次数先快速下降,再趋于平缓。
自动调整学习率
比较流行、简单的想法:
在一开始,设置较大的学习率,使得Loss快速下降,然后逐渐减小学习率,使得Loss慢慢收敛。
学习率的衰减: η t = η t + 1 \eta^t = \frac{\eta}{\sqrt{t+1}} ηt=t+1η
- Adagrad
在学习率衰减的基础上进行改进:
简化可以得到参数更新公式:
w t + 1 = w t − η Σ i = 0 t ( g i ) 2 g t w^{t+1}=w^t-\frac{\eta}{\sqrt{\Sigma^t_{i=0}(g^i)^2}}g^t wt+1=wt−Σi=0t(gi)2ηgt
可能有疑问的地方: g t g^t gt与 Σ i = 0 t ( g i ) 2 \sqrt{\Sigma^t_{i=0}(g^i)^2} Σi=0t(gi)2所起到的作用相反。
一种解释:起到一种反差的效果。

另一种正式的解释:
我们希望参数可以一次更新到位,这只最理想的状态,而参数所在的位置和最低点所在的位置(以loss function为二次函数为例),之间的距离就是 |一次微分|/二次微分。
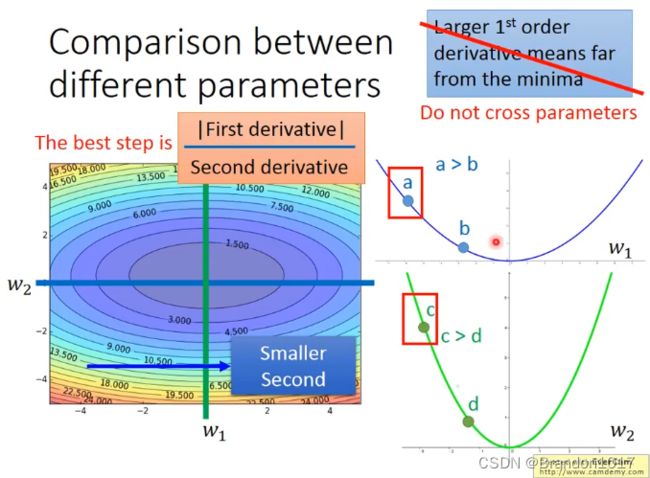
Σ i = 0 t ( g i ) 2 \sqrt{\Sigma^t_{i=0}(g^i)^2} Σi=0t(gi)2这一项在做的事情就是去估计二次微分的大小,用于间接替代二次微分。
随机梯度下降
原来的梯度下降是考虑所有样本的loss计算,而随机梯度下降只考虑某一个参数的loss进行更新。
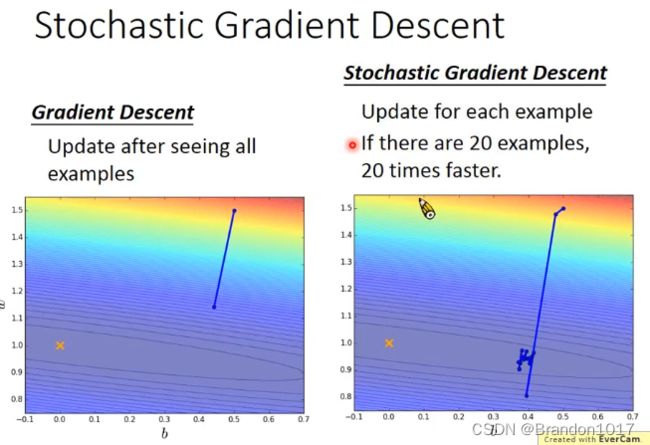
优点:速度更快。
缺点:可能最后无法收敛。
特征缩放(Feature Scaling)
将样本的特征进行缩放(标准化),为了去除量纲的影响。
常见缩放方法:标准化。即减去均值并除以标准差。
梯度下降原理
引入泰勒展开公式,考虑 h ( x ) h(x) h(x)在 x = x 0 x=x_0 x=x0处展开: h ( x ) = h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) + h ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + . . . h(x)=h(x_0)+h'(x_0)(x-x_0)+\frac{h''(x_0)}{2!}(x-x_0)^2+... h(x)=h(x0)+h′(x0)(x−x0)+2!h′′(x0)(x−x0)2+...
于是当 x x x靠近 x 0 x_0 x0时,有 h ( x ) ≈ h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) h(x)\approx h(x_0)+h'(x_0)(x-x_0) h(x)≈h(x0)+h′(x0)(x−x0)。
在二维情境下,上述式子可描述为: h ( x , y ) ≈ h ( x 0 , y 0 ) + ∂ h ( x 0 , y 0 ) ∂ x ( x − x 0 ) + ∂ h ( x 0 , y 0 ) ∂ y ( y − y 0 ) h(x,y)\approx h(x_0,y_0)+\frac{\partial h(x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial h(x_0,y_0)}{\partial y}(y-y_0) h(x,y)≈h(x0,y0)+∂x∂h(x0,y0)(x−x0)+∂y∂h(x0,y0)(y−y0)
那么考虑损失函数 L ( θ ) L(\theta) L(θ)在一点 ( a , b ) (a,b) (a,b),它可以近似为:
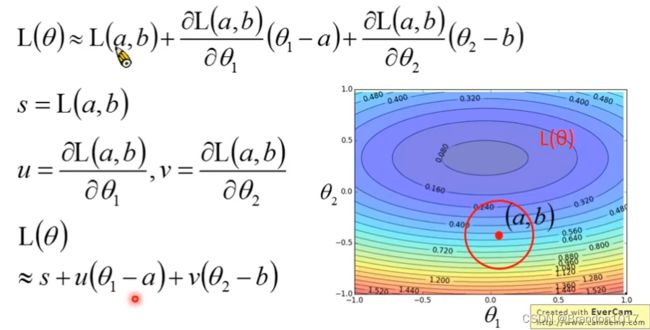

这样我们就从泰勒展开推导到梯度下降。其中最重要的一点就是要在 ( a , b ) (a,b) (a,b)的一个极小的领域中找到最小值,这样才能使得梯度下降,否则可能会失效。而 ( a , b ) (a,b) (a,b)的领域的大小,就对应着学习率,这也是为什么实际中,我们的学习率要设置得相对小才行。