“算法分析与设计”课程设计：回溯法解决八皇后问题并可视化输出（Python实现）

学习目标：

用Python语言和回溯法解决八皇后棋盘问题，并实现可视化输出

---

学习内容：

问题分析

问题描述：八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。 高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。

课设要求

要求：利用回溯法求解八皇后问题，输出该问题的全部解，实现可视化展示。
以上是本次课程设计的要求。

算法思路与解决方案

回溯法特点

回溯法是一种选优搜索法，按照选优条件深度优先搜索，以达到目标。当搜索到某一步时，发现原先选择并不是最优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术称为回溯法，而满足回溯条件的某个状态称为“回溯点”。
回溯法是从初始状态出发，按照深度优先搜索的方式，根据产生子结点的条件约束，搜索问题的解。当发现当前结点不满足求解条件时，就回溯，尝试其他的路径。回溯法是一种“能进则进,进不了则换，换不了则退”的搜索方法。

算法关键技术

（1）定义问题的解空间
n皇后问题解的形式为n元组: {x₁，x₂，…，x_i，…，x_n}，分量x_i表示第i个皇后放置在第i行第x_i列，x_i,的取值为1，2，…，n。例如x₂=5，表示第2个皇后放置在第2行第5列。显约束为不同行。
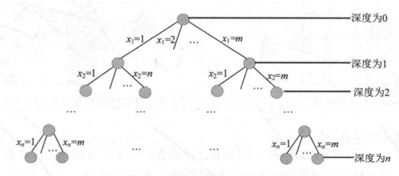
（2）解空间的组织结构
n皇后问题的解空间是一棵m (m=n）叉树，树的深度为n，如图所示。

（3）搜索解空间
· 约束条件
在第t行放置第t个皇后时，第t个皇后的位置不能和前t-1个皇后同列、同斜线。第i个皇后和第j个皇后不同列，即x_i=x_j，并且不同斜线|i一j| != [x_i一x_j]。
· 限界条件
该问题不存在放置方案好坏的情况，所以不需要设置限界条件。
· 搜索过程
从根开始，以深度优先搜索的方式进行搜索。根结点是活结点，并且是当前的扩展结点。在搜索过程中，当前的扩展结点沿纵深方向移向一个新结点,判断该新结点是否满足隐约束。如果满足，则新结点成为活结点，并且成为当前的扩展结点，继续深一层的搜索;如果不满足，则换到该新结点的兄弟结点继续搜索;如果新结点没有兄弟结点，或其兄弟结点已全部搜索完毕，则扩展结点成为死结点，搜索回溯到其父结点处继续进行。搜索过程直到找到问题的根结点变成死结点为止。

算法优化

1．算法复杂度分析
(1)时间复杂度
n皇后问题的解空间是一棵m (m=n)叉树，树的深度为n。最坏情况下，解空间树除了最后一层外，有1+n+n²+…+n^(n-1)=(nⁿ-1)(n-1)≈n^(n-1)个结点需要扩展，而这些结点每个都要扩展n个分支，总的分支个数为n，每个分支都判断约束函数，判断约束条件需要O(n)的时间，因此耗时O(n^(n-1))。在叶子结点处输出当前最优解需要耗时O(n)，在最坏情况下回搜索到每一个叶子结点,叶子个数为nⁿ,故耗时为O(n^(n-1))。因此,时间复杂度为O(n^(n-1))。
(2)空间复杂度
回溯法的另一个重要特性就是在搜索执行的同时产生解空间。在所搜过程中的任何时刻，仅保留从开始结点到当前扩展结点的路径，从开始结点起最长的路径为n。程序中我们使用x[]数组记录该最长路径作为可行解，所以该算法的空间复杂度为O(n)。
2.算法优化拓展
在上面的求解过程中，我们的解空间过于庞大，所以时间复杂度很高，算法效率当然会降低。解空间越小，算法效率越高。因为解空间是我们要搜索解的范围，就像大海捞针，难度很大，在一个水盆里捞针，难度就小了，如果在一个碗里捞针，就更容易了。
我们用四皇后问题来简化表示一下
四皇后问题，显约束为不同行的解空间树如图

显约束可以控制解空间大小，隐约束是在搜索解空间过程中判定可行解或最优解的。
例如x₁=1的分支，x₂就不能再等于1，因为这样就同列了。如果x₁=1、x₂=2，x₃就不能再等于1、2，也就是说x_t的值不能与前t-1个解的取值相同。每层结点产生的孩子数比上一层少一个。四皇后问题，显约束为不同行、不同列的解空间树如图所示。

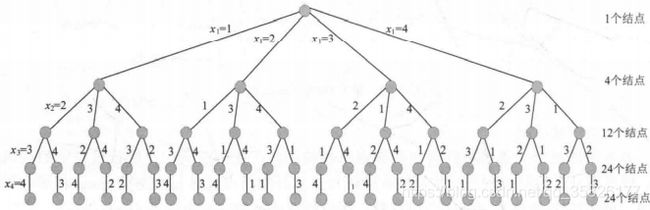
我们可以清楚地看到解空间变小了好多，极大地降低了算法的时间复杂度，此时时间复杂度为O(n³)。

Python代码实现

这里参考了https://blog.csdn.net/weixin_44227192/article/details/106931823?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-0&spm=1001.2101.3001.4242 大佬的代码，并进行了部分修改

import matplotlib.pyplot as plt
import matplotlib
import numpy as np
# ------------------------
#设定中文字符集，解决绘图时中文乱码问题
matplotlib.rcParams['font.sans-serif'] = ['SimHei']

#放置函数
def Queen_set(n):
    global num
    queen_list2=[i+1 for i in queen_list]
    if n==8:
        print("第"+str(num)+"种:",(1,queen_list2[0]),(2,queen_list2[1]),(3,queen_list2[2]),(4,queen_list2[3])
        ,(5,queen_list2[4]),(6,queen_list2[5]),(7,queen_list2[6]),(8,queen_list2[7]))

        plot_chess(queen_list)
        num+=1
        return
    else:
        for i in range(8):
            if check(n,i):
                queen_list.append(i)    #在当前位置放置皇后
                Queen_set(n+1)  #递归，进入下一层搜索
                queen_list.pop() #回溯关键点，清除前一步的错误数据


#检测当前位置是否符合要求
#depth:搜索深度 index:目前的摆放情况
def check(depth,index):
    if depth==0:
        return True
    else:
        for i in range(depth):
            if queen_list[i] == index:   #判断列是否符合
                return False
            #判断对角线规则是否符合
            elif index==queen_list[i]-depth+i or index==queen_list[i]+depth-i:
                return False
        return True

#绘制棋盘并保存求解结果
def plot_chess(result):
    global num
    mat=np.zeros((8,8))
    for i in range(8):
        for j in range(8):
            if result[i]==j:
                mat[i,j]=1
            elif (i+j)%2==0:
                mat[i,j]=-1
            else:
                mat[i,j]=0
    my_cmap=matplotlib.colors.LinearSegmentedColormap.from_list('my_camp',['white','black','red'],3)
    plt.imshow(mat,cmap=my_cmap)
    plt.title("第"+str(num)+"种解法",fontsize=16)
    plt.xticks([])
    plt.yticks([])
    plt.savefig('C:/Users/zhous/Desktop/算法课设/EightQueens Palace/'+str(num)+'.png') #保存图片的路径,自行修改

queen_list = []
num = 1
Queen_set(0)

结果可视化

这里参考了https://blog.csdn.net/weixin_45405128/article/details/102510877?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522162427419916780261924951%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=162427419916780261924951&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_allbaidu_landing_v2~default-1-102510877.first_rank_v2_pc_rank_v29&utm_term=%E7%94%A8matplotlib%E7%94%BB%E6%A3%8B%E7%9B%98&spm=1018.2226.3001.4187 大佬的可视化棋盘代码

#绘制棋盘并保存求解结果
def plot_chess(result):
    global num
    mat=np.zeros((8,8))
    for i in range(8):
        for j in range(8):
            if result[i]==j:
                mat[i,j]=1
            elif (i+j)%2==0:
                mat[i,j]=-1
            else:
                mat[i,j]=0
    my_cmap=matplotlib.colors.LinearSegmentedColormap.from_list('my_camp',['white','black','red'],3)
    plt.imshow(mat,cmap=my_cmap)
    plt.title("第"+str(num)+"种解法",fontsize=16)
    plt.xticks([])
    plt.yticks([])
    plt.savefig('C:/Users/zhous/Desktop/算法课设/EightQueens Palace/'+str(num)+'.png') #保存图片的路径,自行修改

---

学习收获：

解决问题

一、字体问题导致的运行报错
在设定中文字符集，解决绘图时中文乱码问题时，我们遇到了运行报错。

如图所示，所显示的报错意为未找到相应字体。为了解决此问题，我们搜索了CSDN，具体步骤为：

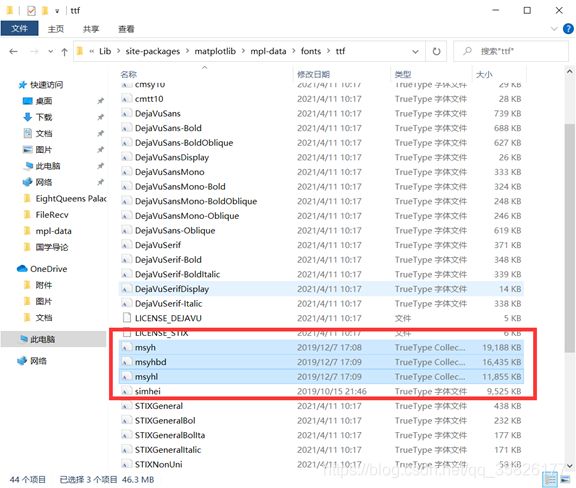
1. 找到Mircosoft YaHei UI字体文件
   一般在C:\Windows\Fonts 里可以看到，如下图
   
2. 将字体文件拷贝至下面的文件夹。里自己的python安装目录F:\Python3.7\Lib\site-packages\matplotlib\mpl-data\fonts\ttf
   拷贝完成后，该文件夹里会有MSYH.TTC 文件
   
3. 修改matplotlibrc文件
   打开matplotlibrc文件
   (1)删除 font.family 前面的 # 并将冒号后面改为“Microsoft YaHei”；
   (2)删除font.sans-serif 前面的 # 并在冒号后面添加“Microsoft YaHei”
   
   
   修改完成后保存，将python关闭，重新启动运行程序，成功解决。

二、输出结果格式不清晰明确
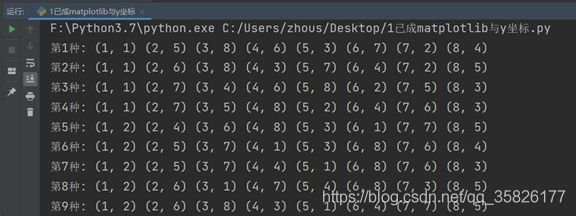
在运行结果中，输出的列表中的每个数表示的是纵向坐标即列坐标，横向坐标默认为从1至8， 如图：

我们将原先代码

print("第"+str(num)+"种:",queen_list2)

修改为

print("第"+str(num)+"种:",(1,queen_list2[0]),(2,queen_list2[1]),(3,queen_list2[2]),(4,queen_list2[3]),(5,queen_list2[4]),(6,queen_list2[5]),(7,queen_list2[6]),(8,queen_list2[7]))

之后，我们成功输出了(x, y)格式的坐标值

---

学习收获：

通过本次课程设计我们很好地解决了八皇后的放置问题，也丰富了我们的编程语言知识，积累了解决问题的经验。

学习产出：

1、 技术笔记 3 遍
2、CSDN 技术博客 1 篇
3、 课程设计报告书 1 篇
4、演示PPT 1 例