李宏毅机器学习误差和梯度下降法
文章目录
-
-
- 误差(Error)
-
- 误差的来源
- 模型的估测
- 偏差和方差的评估
- 偏差大-欠拟合
- 方差大-过拟合
- 模型选择
- 梯度下降法
-
- 梯度下降法的介绍
- 梯度下降法的几个Tips
-
- Tip1:调整学习率
- Tip2:随机梯度下降法
- Tip3:特征缩放
- 梯度下降法的限制
-
误差(Error)
误差的来源
- E r r o r Error Error 的主要来源有两个,分别是 b i a s bias bias 和 v a r i a n c e variance variance (偏差和方差)。
模型的估测
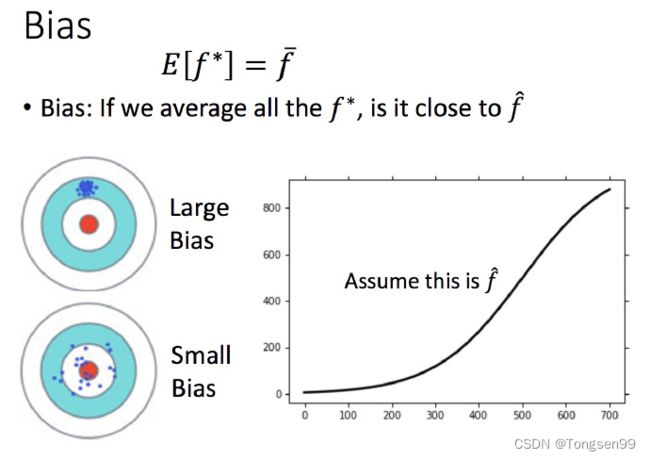
step1~step3 训练得到我们的理想模型 f ∗ f^* f∗, f ∗ f^* f∗ 其实是 f ^ \hat f f^ 的一个估测。

这个过程就像打靶, f ^ \hat f f^ 就是我们的靶心, f ∗ f^* f∗ 就是我们投掷的结果。如上图所示, f ^ \hat f f^ 与 f ∗ f^* f∗ 之间蓝色部分的差距就是偏差和方差导致的。
偏差和方差的评估
假设随机变量X(总体)的数学期望为 μ \mu μ,方差为 σ 2 \sigma^{2} σ2。假设训练样本的均值为 m m m,方差为 s 2 s^{2} s2。
通过抽样采集N个数据点:{ x 1 , x 2 , … , x N x^1 , x^2 , … , x^N x1,x2,…,xN},计算N个数据的平均值(不等于 μ \mu μ,因为只有数据量足够大的情况下,才能逼近 μ \mu μ)。对多个 m m m计算期望值可得到 μ \mu μ,这是无偏估计。
同样抽样采集N个数据点:{ x 1 , x 2 , … , x N x^1 , x^2 , … , x^N x1,x2,…,xN} ,计算N个数据的平均值,然后计算得到样本的方差 s 2 s^2 s2。对多个 s 2 s^2 s2计算期望值,但这却是一个有偏估计。但如果增加N的的个数,就接近于无偏估计了。
- 简单模型的方差比较小(就像射击的时候,每次射击的设置都集中在一个比较小的区域内),复杂模型的方差比较大(散布比较开)。因为简单的模型受到不同训练集的影响是比较小的。
- 简单模型的偏差比较大,复杂模型的偏差比较小。直观的解释:简单的模型函数集的space比较小,所以可能space里面就没有包含靶心,肯定射不中。而复杂的模型函数集的space比较大,可能就包含的靶心,只是没有办法找到确切的靶心在哪,但足够多的,就可能得到真正的靶心。
- b i a s bias bias过大就是欠拟合, v a r i r a n c e varirance varirance过大就是过拟合。
偏差大-欠拟合
此时应该重新设计模型。可以:
- 将更多的特征加进去,比如考虑高度,重量,或者HP值等等。
- 或者考虑更多次幂、更复杂的模型。
如果此时再收集更多的data去训练,也是没有什么帮助的,因为设计的函数集本身就不好,再找更多的训练集也不会更好。
方差大-过拟合
- 采取和训练更多的数据。
- 采用正则化(希望参数越小越好)。正则化可能会使得 b i a s bias bias增加,使得函数空间不包括目标函数target。
模型选择
- 在偏差和方差之间需要一个权衡,使得总错误最小
一个好方法是使用交叉验证,把训练集划分为训练集和验证集。通过训练数据得到模型,然后把模型放到验证集上面进行验证,假设在Model 1,Model 2,Model 3中得到最佳模型为Model 3。然后再把Model 3放到Training Set所有数据上跑,得到模型的参数。需要注意的是,不能再跟据public Testing Set的结果再去重新选模型,如果这么做的话,就会使得模型的泛化能力下降。
N-折交叉验证:

在上图中,这三份中训练结果Average错误是模型1最好,再用全部训练集训练模型1。
梯度下降法
梯度下降法的介绍
- 梯度下降是一种非常通用的优化算法,能够为大范围的问题找到最优解。梯度下降的中心思想就是迭代地调整参数从而使成本函数最小化。
假设你迷失在山上的浓雾之中,你能感觉到的只有你脚下路面的坡度。快速到达山脚的一个策略就是沿着最陡的方向下坡。这就是梯度下降的做法:通过测量参数向量θ相关的误差函数的局部梯度,并不断沿着降低梯度的方向调整,直到梯度降为0,到达最小值! 具体来说,首先使用一个随机的θ值(这被称为随机初始化),然后逐步改进,每次踏出一步,每一步都尝试降低一点成本函数(如MSE),直到算法收敛出一个最小值。
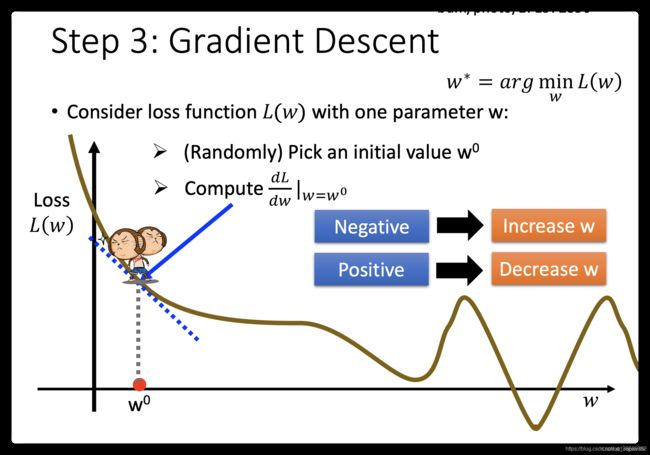
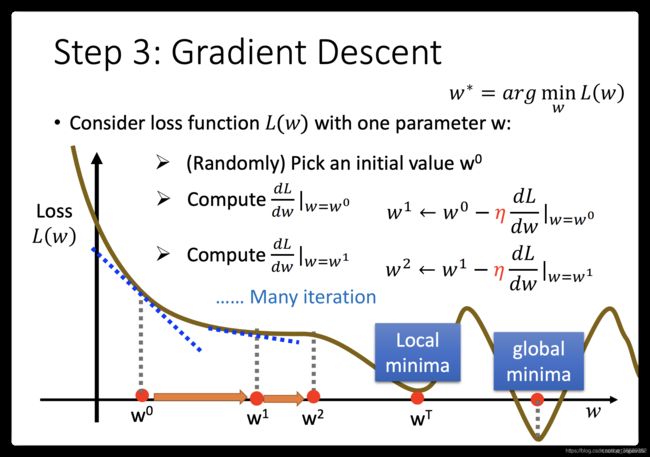
这里需要引入一个学习率的概念:即移动的步长 η \eta η
大致步骤如下:
- 步骤1:随机选取一个 w 0 w^0 w0
- 步骤2:计算微分,也就是当前的斜率,根据斜率来判定移动的方向:
- 大于0减小 w w w值
- 小于0增加 w w w值
- 步骤3:根据学习率移动
- 重复步骤2和步骤3,直到找到最低点
换言之,即为最优化问题:
θ ∗ = arg min θ L ( θ ) \theta^∗= \underset{ \theta }{\operatorname{arg\ min}} L(\theta) θ∗=θarg minL(θ)
其中:
- L L L :loss function(损失函数)
- θ \theta θ :parameters(参数)
我们的任务是要找一组参数 θ \theta θ ( θ \theta θ 指代一堆参数,同 w w w 和 b b b),让损失函数越小越好。
具体步骤如下(假设 θ \theta θ 有里面有两个参数 θ 1 , θ 2 \theta_1, \theta_2 θ1,θ2):
- step1:随机选取初始值
θ 0 = [ θ 1 0 θ 2 0 ] \theta^0 = \begin{bmatrix} \theta_1^0 \\ \theta_2^0\end{bmatrix} θ0=[θ10θ20] - step2:分别计算初始点处,两个参数对 L L L 的偏微分,然后 θ 0 \theta^0 θ0 减掉 η \eta η 乘上偏微分( ▽ L ( θ ) \triangledown L(\theta) ▽L(θ) 即为梯度。)的值,得到一组新的参数。
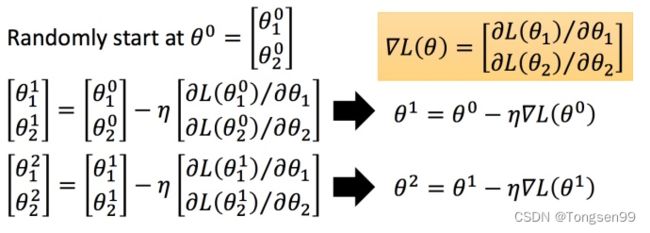
- step3:同理反复进行这样的计算。

- 学习率太低导致迭代至收敛太慢
- 学习率太高导致直接越过谷底,算法发散
不过对于局部最优点,线性回归问题不大,因为线性回归中的损失函数为凸函数,所以不存在局部最优点。
梯度下降法的几个Tips
Tip1:调整学习率
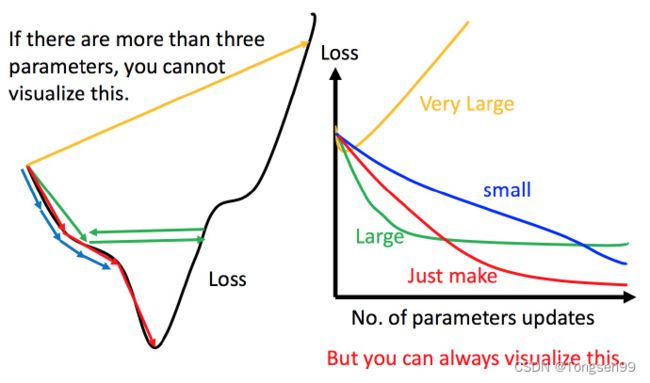
上图为不同大小的学习率 η \eta η的参数和损失值的曲线。
自适应学习率:随着次数的增加,通过一些因子来减少学习率。
- 通常刚开始,初始点会距离最低点比较远,所以使用大一点的学习率
- update好几次参数之后,比较靠近最低点了,此时减少学习率
- 比如 η t = η t t + 1 \eta^t =\frac{\eta^t}{\sqrt{t+1}} ηt=t+1ηt, t t t 是次数。随着次数的增加, η t \eta^t ηt 减小
注意,学习率不能是一个值通用所有特征,不同的参数需要不同的学习率。
Adagrad 算法:每个参数的学习率都除上之前微分的均方根。
普通梯度下降为:
g t = ∂ L ( θ t ) ∂ w g^t =\frac{\partial L(\theta^t)}{\partial w} gt=∂w∂L(θt)
η t = η t t + 1 \eta^t =\frac{\eta^t}{\sqrt{t+1}} ηt=t+1ηt
w t + 1 ← w t − η t g t w^{t+1} \leftarrow w^t -η^tg^t wt+1←wt−ηtgt
- w w w 是一个参数
Adagrad可以做的更好:
w t + 1 ← w t − η t σ t g t w^{t+1} \leftarrow w^t -\frac{η^t}{\sigma^t}g^t wt+1←wt−σtηtgt
- σ t \sigma^t σt :之前参数的所有微分的均方根。对于每个参数都是不一样的。
举个例子:
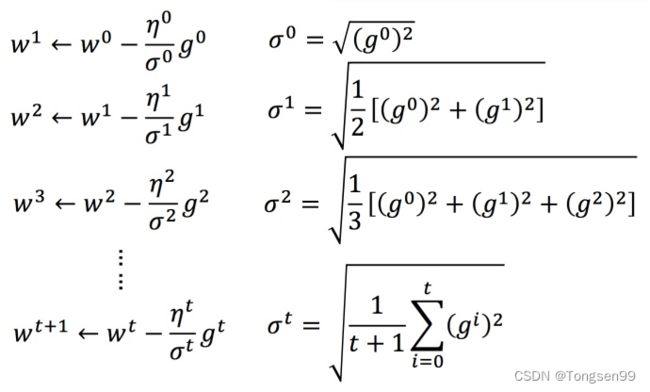
将 Adagrad 的式子进行化简:
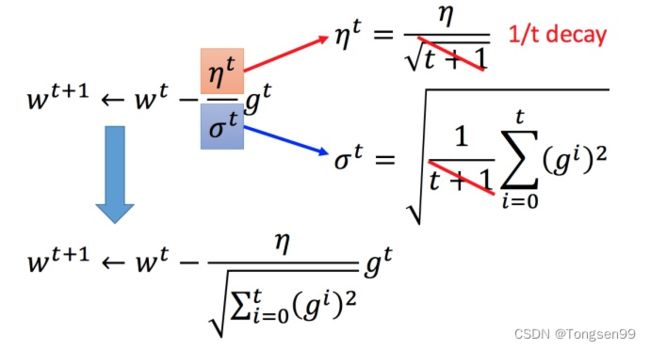
矛盾:在 Adagrad 中,当梯度越大的时候,步伐应该越大,但下面分母又导致当梯度越大的时候,步伐会越小。

梯度越大,所需要的步幅越大?前提条件是同一个参数。
跨参数可能会得到错误的结论,即多参数下结论不一定成立,对比不同参数如下:
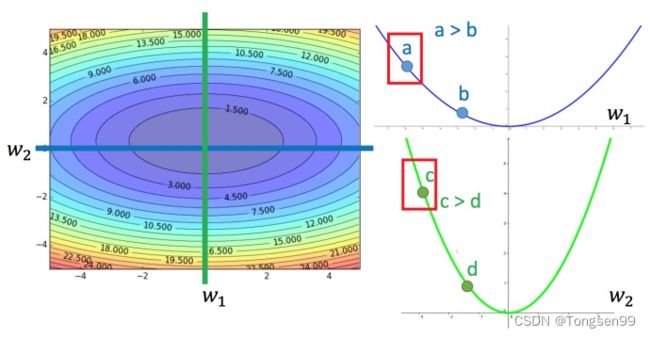
在上图中,左边是两个参数的损失函数,颜色代表损失函数的值。如果只考虑参数 w 1 w_1 w1,就像图中蓝色的线,得到右边上图结果;如果只考虑参数 w 2 w_2 w2,就像图中绿色的线,得到右边下图的结果。确实对于 a a a和 b b b,结论(梯度越大,所需要的步幅越大)是成立的,同理 c c c和 d d d也成立。但是如果对比 a a a和 c c c,就不成立了, c c c梯度 比 a a a大,但 c c c距离最低点是比较近的。
再回到之前的 Adagrad:
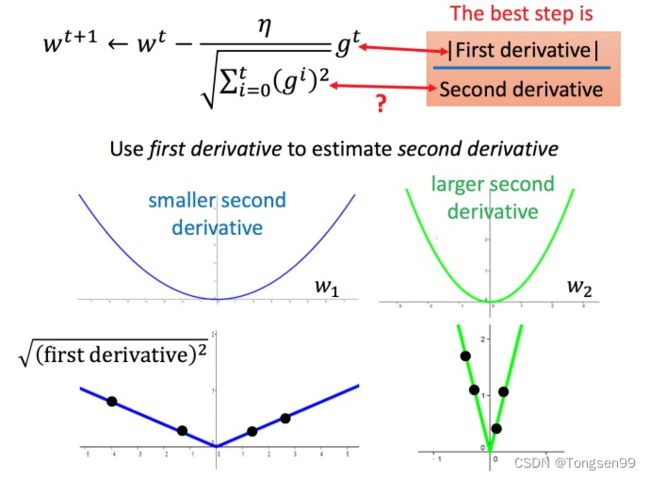
对于 ∑ i = 0 t ( g i ) 2 \sqrt{\sum_{i=0}^t(g^i)^2} ∑i=0t(gi)2 就是希望再尽可能不增加过多运算的情况下模拟二次微分。(如果计算二次微分,在实际情况中可能会增加很多的时间消耗)。
Tip2:随机梯度下降法
根据计算梯度的样本个数,可分为批量梯度下降(全部样本)、小批量梯度下降(batch个数的样本)、随机梯度下降(单个样本)。
其中:
- 随机梯度下降法更快,因为损失函数不需要处理训练集所有的数据。
选取一个例子 x n x^n xn:
L = ( y ^ n − ( b + ∑ w i x i n ) ) 2 L=(\hat y^n-(b+\sum w_ix_i^n))^2 L=(y^n−(b+∑wixin))2
θ i = θ i − 1 − η ▽ L n ( θ i − 1 ) \theta^i =\theta^{i-1}- \eta\triangledown L^n(\theta^{i-1}) θi=θi−1−η▽Ln(θi−1)
此时不需要像之前那样对所有的数据进行处理,只需要计算某一个例子的损失函数 L n L^n Ln,就可以赶紧update 梯度。
与普通梯度下降法对比:
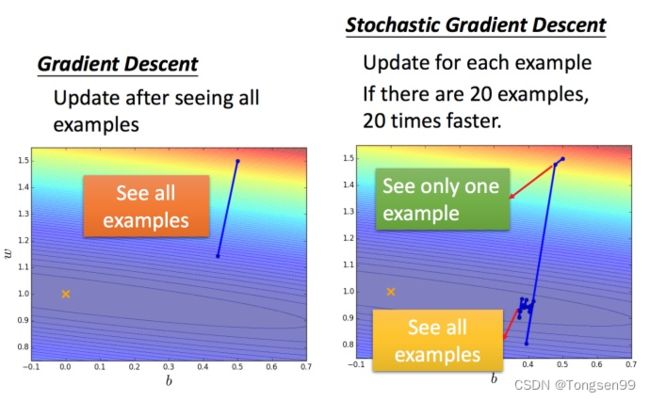
Tip3:特征缩放
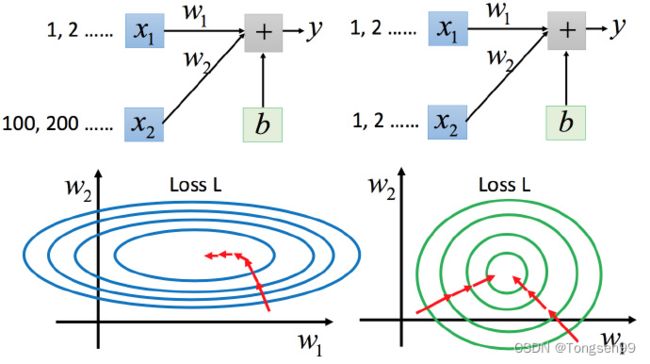
- 上图左边是 x 1 x_1 x1 的scale比 x 2 x_2 x2 要小很多,所以当 w 1 w_1 w1 和 w 2 w_2 w2 做同样的变化时, w 1 w_1 w1 对 y y y 的变化影响是比较小的, w 2 w_2 w2 对 y y y 的变化影响是比较大的。
- 坐标系中是两个参数的error surface(现在考虑左边蓝色),因为 w 1 w_1 w1 对 y y y 的变化影响比较小,所以 w 1 w_1 w1 对损失函数的影响比较小, w 1 w_1 w1 对损失函数有比较小的微分,所以 w 1 w_1 w1 方向上是比较平滑的。同理 w 2 w_2 w2 对 y y y 的影响比较大,所以 w 2 w_2 w2 对损失函数的影响比较大,所以在 w 2 w_2 w2 方向有比较尖的峡谷。
- 上图右边是两个参数scaling比较接近,右边的绿色图就比较接近圆形。
- 左边的梯度下降并不是向着最低点方向走的,而是顺着等高线切线法线方向走的。但绿色就可以向着圆心(最低点)走,这样做参数更新也是比较有效率。
特征缩放的两种方法:归一化和标准化。
归一化:将数据映射到(0,1)上。
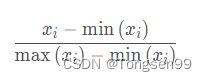
标准化:类似于标准正态分布过程,将这列数据处理成均值为0,方差为1。
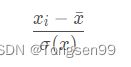
梯度下降法的限制
- 容易陷入局部最优点
- 可能卡在不是极值,但微分值是0的地方
- 可能实际中只是当微分值小于某一个数值就停下来了,但这里只是比较平缓,并不是极值点