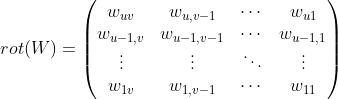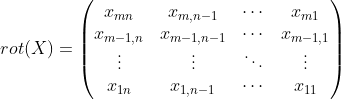NNDL 作业7：第五章课后题（1×1 卷积核 | CNN BP）
目录
习题5-2 证明宽卷积具有交换性，即公式:
习题5-3 分析卷积神经网络中用1×1的卷积核的作用
习题5-4 对于一个输入为100×100×256的特征映射组，使用3×3的卷积核，输出为100×100×256的特征映射组的卷积层，求其时间和空间复杂度。如果引入一个1×1的卷积核，先得到100×100×64的特征映射，再进行3×3的卷积，得到100×100×256的特征映射组，求其时间和空间复杂度。
习题5-7 忽略激活函数，分析卷积网络中卷积层的前向计算和反向传播是一种转置关系
推导CNN反向传播算法（选做）
设计简易CNN模型，分别用Numpy、Pytorch实现卷积层和池化层的反向传播算子，并代入数值测试.(选做)
总结
参考链接
习题5-2 证明宽卷积具有交换性，即公式:
证明：
不失一般性，设：
则：
，
两端各补
和
个零，得到
:
两端各补
和 
个零 ， 得到
:
由定义：
将
代入，计算可得：
因此：
即：
原始得证。
习题5-3 分析卷积神经网络中用1×1的卷积核的作用
- 增加网络的深度，添加非线性
可以减少网络模型参数，增加网络层深度，一定程度上提升模型的表征能力。1*1卷积核，可以在保持feature map尺度不变的（即不损失分辨率）的前提下大幅增加非线性特性（利用后接的非线性激活函数），把网络做的很deep。
- 升维或者降维
feature map和1*1的卷积核做卷积时，只需要考虑当前像素即可，并不需要考虑周围的像素值。因此第一个作用主要是可以用来调节feature map的通道数，对不同通道上的像素点进行线性组合，即可实现feature map的升维或降维功能，这也是通道见信息的交互和整合过程。
- 减少网络参数，是成倍数减少
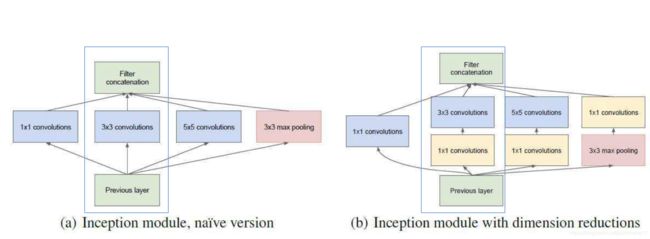
减少模型参数这一想法最早应该是在GoogleNet中提出的，假设给定如下两个Inception模块：
如上图，现在蓝色方框中，左侧是3∗3的卷积，而右侧是1∗1 和一个3∗3的卷积。两者的功能是一样的，即得到的输出维度相同。现在要计算两者的参数量，直觉上来说，单个3∗3的卷积参数似乎较少，但事实真的如此吗？
我们假设Previous Layer得到结果的维度是（96, 28, 28），即这个Inception模块的输入是96通道，长宽均为28的feature map，卷积后输出通道为48。假设经过左侧和右侧模块的方框所需要的计算参数分别为p1，p2，则p1和p2的计算公式如下：
p1 = 96 ∗ 3 ∗ 3 ∗ 48 = 41472
右图中第一个1 ∗ 1 1*11∗1卷积可以先将原始输入降维，假设这里降到32维，则：
p2 = 96 ∗ 1 ∗ 1 ∗ 32 + 32 ∗ 3 ∗ 3 ∗ 48 = 16896
注：卷积核的通道数与输入的feature map一致，而卷积核的个数与输出channel一致。
我们惊奇的发现，反而是第二种采用了1 ∗ 1 1*11∗1和3 ∗ 3 3*33∗3两次卷积的结构，拥有更少的训练参数。由此可见，虽然加入了这额外的1 ∗ 1 1*11∗1的卷积层，但竟然可以减少训练的参数。
- 跨通道信息交互（channal的变换）
我们还可以用另一种角度去理解1*1卷积，可以把它看成是一种全连接，如下图：
第一层有6个神经元，分别是a1—a6，通过全连接之后变成5个，分别是b1—b5，第一层的六个神经元要和后面五个实现全连接，本图中只画了a1—a6连接到b1的示意，可以看到，在全连接层b1其实是前面6个神经元的加权和，权对应的就是w1—w6，到这里就很清晰了：
第一层的6个神经元其实就相当于输入特征里面那个通道数：6，而第二层的5个神经元相当于1*1卷积之后的新的特征通道数：5。
习题5-4 对于一个输入为100×100×256的特征映射组，使用3×3的卷积核，输出为100×100×256的特征映射组的卷积层，求其时间和空间复杂度。如果引入一个1×1的卷积核，先得到100×100×64的特征映射，再进行3×3的卷积，得到100×100×256的特征映射组，求其时间和空间复杂度。
时间复杂度：时间复杂度即模型的运行次数。
空间复杂度：空间复杂度即模型的参数数量。
①时间复杂度=100*100*3*3**256*256=5898240000
空间复杂度=3*3**256*256+100*100*256=3149824
②时间复杂度=100*100*1*1*256*64+100*100*3*3*64*256=1638400000
空间复杂度=1*1*256*64+100*100*64+3*3*64*256+100*100*256=3363840
习题5-7 忽略激活函数，分析卷积网络中卷积层的前向计算和反向传播是一种转置关系
以一个3×3的卷积核为例，输入为X输出为Y
将4×4的输入特征展开为16×1的矩阵，y展开为4×1的矩阵，将卷积计算转化为矩阵相乘
由
而 
即
所以
再看一下上面的Y=CX可以发现忽略激活函数时卷积网络中卷积层的前向计算和反向传播是一种转置关系。
推导CNN反向传播算法（选做）
1.已知池化层的
，求出上一隐藏层的
在前向传播过程中，池化层一般会使用Max或Average对输入进行池化，池化的区域大小给定。现在我们要从缩小区域后的，还原之前较大区域对应的误差。
在反向传播时，我们首先会把δlδl的所有子矩阵矩阵大小还原成池化之前的大小，然后如果是MAX，则把δlδl的所有子矩阵的各个池化局域的值放在之前做前向传播算法得到最大值的位置。如果是Average，则把δlδl的所有子矩阵的各个池化局域的值取平均后放在还原后的子矩阵位置。这个过程一般叫做upsample。
用一个例子可以很方便的表示：假设我们的池化区域大小是2x2。的第k个子矩阵为：
如果池化区域大小为2*2，我们先将做还原，即变成：
1）如果是MAX，假设我们之前在前向传播时记录的最大值位置分别是左上，右下，右上，左下，则转换后的矩阵为：
2） 如果是Average，则进行平均：转换后的矩阵为：
3）这样我们就得到了卷积层后一层upsample后的，由于池化层没有W、b参数需要学习，是一个分辨率变化过程，使用的是线性激活函数。所以
结论：由池化层的结果向前一层传播的话，由于池化层没有参数需要学习，但是由于池化操作造成了数据维度的变化，所以需要有一个数据的上采样过程，上采样过程跟池化的方法有关。上采样之后，由于池化是个线性函数的过程，所以要求针对上一层的z的梯度，中间只有一个上一层的z到a的激活函数，因此得出上面的结论。
2.已知卷积层的，求出上一隐藏层的
我们首先写出卷积层的前向传播过程公式，假设
为卷积层前的输入数据，
为经过一个卷积核和激活函数的操作结果
我们以一个l-1层为3*3的矩阵为例，卷积核W^l为2*2，滑动步伐为1，则输出为2*2的矩阵。简化b^l为0，左侧为l-1层，右侧为l层
首先我们从前面的DNN可以得出求解对于W和b的梯度变化，求该层 的是关键的，而且层与层之间是递推的关系
进而现在如果我们从最后一层递推到前面的层的话， 成为了需要关键计算的，对于普通的DNN层的话，结果就是上式中去掉的计算结果，下面我们讨论卷积层前后的z^l-1和z^l的关系。
我们依然以上面的例子为例，3*3的a^l-1输入，2*2卷积核，1步长，输出为2*2的z^l，我们把卷积前后的结果展开，左侧为卷积后的结果z^l，右侧为卷积前的结果a^l-1，我们先讨论，z^l和a^l-1的关系
根据之前的递推公式，我们也可以得出
从上面的公式我们可以得出例子中每个的计算结果。由于上一层的输入包含9个数据，a11与公式1有关，a12与公式1、公式2有关，a13与公式2有关，a21与公式1、公式3有关，a22与四个公式都有关，a23与公式2、公式4有关，a31与公式3有关，a32与公式3、公式4有关，a33与公式4有关。所以上一层a的梯度误差可能和多个输出相关。
上面的操作可以用一个卷积的形式来表示，为了符合梯度计算，我们在误差矩阵周围添加了一圈0。然后将卷积核翻转后（上下、左右）进行卷积操作，便算出来了上一层输入的误差
现在我们算出了卷积层之间过渡的递推公式，即卷积层后的输出的误差和旋转卷积核的卷积结果（
到
的计算，
）。所以我们现在已经求出了卷积层连续过渡的关键因素（等同于DNN中的
到
）。
设计简易CNN模型，分别用Numpy、Pytorch实现卷积层和池化层的反向传播算子，并代入数值测试.(选做)
卷积层的反向传播实现：
from typing import Dict, Tuple
import numpy as np
import pytest
import torch
def conv2d_forward(input: np.ndarray, weight: np.ndarray, bias: np.ndarray,
stride: int, padding: int) -> Dict[str, np.ndarray]:
"""2D Convolution Forward Implemented with NumPy
Args:
input (np.ndarray): The input NumPy array of shape (H, W, C).
weight (np.ndarray): The weight NumPy array of shape
(C', F, F, C).
bias (np.ndarray | None): The bias NumPy array of shape (C').
Default: None.
stride (int): Stride for convolution.
padding (int): The count of zeros to pad on both sides.
Outputs:
Dict[str, np.ndarray]: Cached data for backward prop.
"""
h_i, w_i, c_i = input.shape
c_o, f, f_2, c_k = weight.shape
assert (f == f_2)
assert (c_i == c_k)
assert (bias.shape[0] == c_o)
input_pad = np.pad(input, [(padding, padding), (padding, padding), (0, 0)])
def cal_new_sidelngth(sl, s, f, p):
return (sl + 2 * p - f) // s + 1
h_o = cal_new_sidelngth(h_i, stride, f, padding)
w_o = cal_new_sidelngth(w_i, stride, f, padding)
output = np.empty((h_o, w_o, c_o), dtype=input.dtype)
for i_h in range(h_o):
for i_w in range(w_o):
for i_c in range(c_o):
h_lower = i_h * stride
h_upper = i_h * stride + f
w_lower = i_w * stride
w_upper = i_w * stride + f
input_slice = input_pad[h_lower:h_upper, w_lower:w_upper, :]
kernel_slice = weight[i_c]
output[i_h, i_w, i_c] = np.sum(input_slice * kernel_slice)
output[i_h, i_w, i_c] += bias[i_c]
cache = dict()
cache['Z'] = output
cache['W'] = weight
cache['b'] = bias
cache['A_prev'] = input
return cache
def conv2d_backward(dZ: np.ndarray, cache: Dict[str, np.ndarray], stride: int,
padding: int) -> Tuple[np.ndarray, np.ndarray, np.ndarray]:
"""2D Convolution Backward Implemented with NumPy
Args:
dZ: (np.ndarray): The derivative of the output of conv.
cache (Dict[str, np.ndarray]): Record output 'Z', weight 'W', bias 'b'
and input 'A_prev' of forward function.
stride (int): Stride for convolution.
padding (int): The count of zeros to pad on both sides.
Outputs:
Tuple[np.ndarray, np.ndarray, np.ndarray]: The derivative of W, b,
A_prev.
"""
W = cache['W']
b = cache['b']
A_prev = cache['A_prev']
dW = np.zeros(W.shape)
db = np.zeros(b.shape)
dA_prev = np.zeros(A_prev.shape)
_, _, c_i = A_prev.shape
c_o, f, f_2, c_k = W.shape
h_o, w_o, c_o_2 = dZ.shape
assert (f == f_2)
assert (c_i == c_k)
assert (c_o == c_o_2)
A_prev_pad = np.pad(A_prev, [(padding, padding), (padding, padding),
(0, 0)])
dA_prev_pad = np.pad(dA_prev, [(padding, padding), (padding, padding),
(0, 0)])
for i_h in range(h_o):
for i_w in range(w_o):
for i_c in range(c_o):
h_lower = i_h * stride
h_upper = i_h * stride + f
w_lower = i_w * stride
w_upper = i_w * stride + f
input_slice = A_prev_pad[h_lower:h_upper, w_lower:w_upper, :]
# forward
# kernel_slice = W[i_c]
# Z[i_h, i_w, i_c] = np.sum(input_slice * kernel_slice)
# Z[i_h, i_w, i_c] += b[i_c]
# backward
dW[i_c] += input_slice * dZ[i_h, i_w, i_c]
dA_prev_pad[h_lower:h_upper,
w_lower:w_upper, :] += W[i_c] * dZ[i_h, i_w, i_c]
db[i_c] += dZ[i_h, i_w, i_c]
if padding > 0:
dA_prev = dA_prev_pad[padding:-padding, padding:-padding, :]
else:
dA_prev = dA_prev_pad
return dW, db, dA_prev
@pytest.mark.parametrize('c_i, c_o', [(3, 6), (2, 2)])
@pytest.mark.parametrize('kernel_size', [3, 5])
@pytest.mark.parametrize('stride', [1, 2])
@pytest.mark.parametrize('padding', [0, 1])
def test_conv(c_i: int, c_o: int, kernel_size: int, stride: int, padding: str):
# Preprocess
input = np.random.randn(20, 20, c_i)
weight = np.random.randn(c_o, kernel_size, kernel_size, c_i)
bias = np.random.randn(c_o)
torch_input = torch.from_numpy(np.transpose(
input, (2, 0, 1))).unsqueeze(0).requires_grad_()
torch_weight = torch.from_numpy(np.transpose(
weight, (0, 3, 1, 2))).requires_grad_()
torch_bias = torch.from_numpy(bias).requires_grad_()
# forward
torch_output_tensor = torch.conv2d(torch_input, torch_weight, torch_bias,
stride, padding)
torch_output = np.transpose(
torch_output_tensor.detach().numpy().squeeze(0), (1, 2, 0))
cache = conv2d_forward(input, weight, bias, stride, padding)
numpy_output = cache['Z']
assert np.allclose(torch_output, numpy_output)
# backward
torch_sum = torch.sum(torch_output_tensor)
torch_sum.backward()
torch_dW = np.transpose(torch_weight.grad.numpy(), (0, 2, 3, 1))
torch_db = torch_bias.grad.numpy()
torch_dA_prev = np.transpose(torch_input.grad.numpy().squeeze(0),
(1, 2, 0))
dZ = np.ones(numpy_output.shape)
dW, db, dA_prev = conv2d_backward(dZ, cache, stride, padding)
assert np.allclose(dW, torch_dW)
assert np.allclose(db, torch_db)
assert np.allclose(dA_prev, torch_dA_prev)池化层的反向传播实现：
import numpy as np
from module import Layers
class Pooling(Layers):
def __init__(self, name, ksize, stride, type):
super(Pooling).__init__(name)
self.type = type
self.ksize = ksize
self.stride = stride
def forward(self, x):
b, c, h, w = x.shape
out = np.zeros([b, c, h//self.stride, w//self.stride])
self.index = np.zeros_like(x)
for b in range(b):
for d in range(c):
for i in range(h//self.stride):
for j in range(w//self.stride):
_x = i *self.stride
_y = j *self.stride
if self.type =="max":
out[b, d, i, j] = np.max(x[b, d, _x:_x+self.ksize, _y:_y+self.ksize])
index = np.argmax(x[b, d, _x:_x+self.ksize, _y:_y+self.ksize])
self.index[b, d, _x +index//self.ksize, _y +index%self.ksize ] = 1
elif self.type == "aveg":
out[b, d, i, j] = np.mean((x[b, d, _x:_x+self.ksize, _y:_y+self.ksize]))
return out
def backward(self, grad_out):
if self.type =="max":
return np.repeat(np.repeat(grad_out, self.stride, axis=2),self.stride, axis=3)* self.index
elif self.type =="aveg":
return np.repeat(np.repeat(grad_out, self.stride, axis=2), self.stride, axis=3)/(self.ksize * self.ksize)总结
这次实验手动推导并反复理解反向传播的公式和含义，对于CNN的反向传播理解加深，推导了宽卷积的交换性，这里参考了老师的推导过程，同时对于1*1的卷积核理解加深，学习了卷积神经网络中用1×1的卷积核的作用，且1×1卷积核可以增加模型非线性表达能力，掌握了时间复杂度和空间复杂度的计算过程，收获很大。
参考链接
NNDL作业 宽卷积具有交换性_HBU_David的博客-CSDN博客
如何理解卷积神经网络中的1*1卷积_zxucver的博客-CSDN博客_1*1卷积
卷积神经网络中1*1卷积的作用_m0_61899108的博客-CSDN博客
CNN的反向传播过程的推导（池化层、卷积层）_legend_hua的博客-CSDN博客