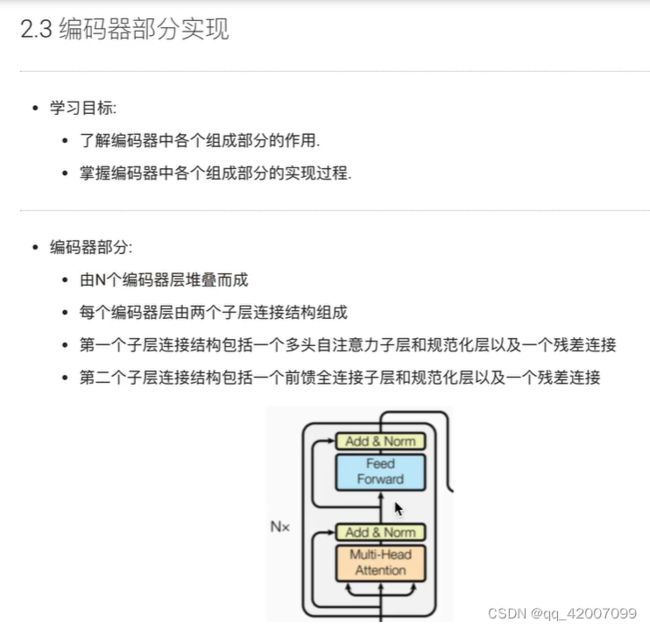
Transformer编码部分的解析

1.掩码张量 

​​​

 

def subsequent_mask(size):
    attn_shape = (1,size,size)  #代表掩码张量的后两个维度
    
    #先np.one构建一个全1的矩阵，然后利用np.triu()形成上三角
    subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
    return torch.from_numpy(1-subsequent_mask)  #使得三角矩阵翻转

size = 5
sm = subsequent_mask(size)
print(sm)

>>>tensor([[[1, 0, 0, 0, 0],
            [1, 1, 0, 0, 0],
            [1, 1, 1, 0, 0],
            [1, 1, 1, 1, 0],
            [1, 1, 1, 1, 1]]], dtype=torch.uint8)

其中，np.triu(a, k)是取矩阵a的上三角数据，但这个三角的斜线位置由k的值确定。

np.triu([[1,2,3],[4,5,6],[7,8,9],[10,11,12]]，k=0)

>>>>array([[1, 2, 3],
           [0, 5, 6],
           [0, 0, 9],
           [0, 0, 0]])


np.triu([[1,2,3],[4,5,6],[7,8,9],[10,11,12]],k=1)
>>>>array([[0, 2, 3],
           [0, 0, 6],
           [0, 0, 0],
           [0, 0, 0]])


np.triu([[1,2,3],[4,5,6],[7,8,9],[10,11,12]],k=-1)
>>>>>array([[ 1,  2,  3],
           [ 4,  5,  6],
           [ 0,  8,  9],
           [ 0,  0, 12]])

当np.triu(a, k = 1)时，得到主对角线向上平移一个距离的对角线，也叫右上对角线及其以上的数据。

当np.triu(a, k = -1)时，得到主对角线向下平移一个距离的对角线，也叫左下对角线及其以上的数据，

2.注意力机制

#query, key, value注意力的三个输入
def attention(query, key, value,mask=None, dropout=None):
     # 获取query的最后一维的大小，一般情况下就等同于我们的词嵌入维度
    d_k = query.size(-1)
    
    #key需要最后两个维度转变（满足矩阵计算规则），再除以缩放系数
    # 得到注意力的得分张量scores
    scores = torch.matmul(query, key.transpose(-2,-1))/math.sqrt(d_k)
    
    if mask is not None:
        # 使用tensor的masked_fill方法，将掩码张量和scores张量每个位置一一比较
        # 如果掩码张量处为0 则对应的score张量用-1e9替换
        scores = scores.masked_fill(mask==0, -1e9)
    p_atten = F.softmax(scores, dim=-1)
    if dropout is not None:       #是否使用dropout进行随机置零
        p_atten = dropout(p_atten)              #传入p_atten进行置零
        
        #最后，根据公式将p_attn与value张量相乘获得最终的query注意力输出，同时返回注意力张量
    return torch.matmul(p_atten, value.float()), p_atten  

query = key = value = pe_result
attn, p_atten =  attention(query, key, value)
print('attn',attn)
print(attn.shape)
print('p_atten',p_atten)
print(p_atten.shape)

当query=key=value为自注意力机制。

.mask_fill(x==0,-1e9)表示矩阵x值为0的地方用-1e9填充

x = torch.zeros(4,5)
print(x)
x.masked_fill(x==0, -1e9)


>>>tensor([[0., 0., 0., 0., 0.],
           [0., 0., 0., 0., 0.],
           [0., 0., 0., 0., 0.],
           [0., 0., 0., 0., 0.]])

>>>tensor([[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
          [-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
          [-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
          [-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09]])

3.多头注意力机制

 

多头注意力机制的作用:
·这种结构设计能让每个注意力机制去优化每个词汇的不同特征部分，从而均衡同一种注意力机制可能产生的偏差，让词义拥有来自更多元的表达，实验表明可以从而提升模型效果。多头注意力机制最重要的是将词嵌入向量进行切分

需要使用clone函数将他们一同初始化到一个网络层列表对象中 

#定义一个克隆函数，再多头中有多个结构相同的线性层
def clone(module, N):
    """
    module:目标网络层
    N：克隆的数量
    """
    #在函数中，我们通过for循环对module进行N次深度拷贝，使其每个module成为独立的层，
    #然后将其放在nn. ModuleList类型的列表中存放.
    return nn.ModuleList({copy.deepcopy(module) for _ in range(N)})

class MultiHeadAttention(nn.Module):
    """在类的初始化时，会传入三个参数，head代表头数,embedding_dim代表词嵌入的维度,
        dropout代表进行dropout操作时置0比率，默认是0.1."" """
    def __init__(self, head, embedding_dim, dropout=0.1):
        super(MultiHeadAttention,self).__init__()
        
        #在函数中，首先使用了一个测试中常用的assert语句，判断h是否能被d_model整除,
        #这是因为我们之后要给每个头分配等量的词特征.也就是embedding_dim/head个.
        assert embedding_dim % head ==0
        
        #得到每个头分配的词嵌入维度
        self.d_k = embedding_dim // head
        
        self.head = head
        
        #然后获得线性层对象，通过nn的Linear实例化，它的内部变换矩阵是embedding_dim×embedding_dim 
        #为什么是四个呢，这是因为在多头注意力中，Q，K，V各需要一个，最后concat拼接的矩阵还需要一个，
        self.linears = clones(nn.Linear(embedding_dim, embedding_dim),4)
        
        # self.attn为None，它代表最后得到的注意力张量，现在还没有结果所以为None.
        self.attn = None
        self.dropout=nn.Dropout(p=dropout)
        
    def forward(self,query, key, value,mask=None):
        if mask is not None:
            mask = mask.unsqueeze(1)
            
        #接着，我们获得一个batch_size的变量，他是query尺寸的第1个数字，代表有多少条样本.
        batch_size = query.size(0)
        
        #首先利用zip将输入QKV与三个线性层组到一起，然后使用for循环，将输入QKV分别传到线性层中，
        #做完线性变换后，开始为每个头分割输入，这里使用view方法对线性变换的结果进行维度重塑，多加了一个维度
        #这样就意味着每个头可以获得一部分词特征组成的句子，其中的-1代表自适应维度，
        #计算机会根据这种变换自动计算这里的值.然后对第二维和第三维进行转置操作，
        #为了让代表句子长度维度和词向量维度能够相邻，这样注意力机制才能找到词义与句子位置的关系，
        # 从attention函数中可以看到，利用的是原始输入的倒数第一和第二维.这样我们就得到了每个头的输入

        query,key,value =[model(x).view(batch_size, -1, self.head, self.d_k).transpose(1,2)
        for model, x in zip(self.linears, (query, key, value))]
        
        #得到每个头的输入后，接下来就是将他们传入到attention中，
        #这里直接调用我们之前实现的attention函数.同时也将mask和dropout传入其中．
        x, self.attn = attention(query, key, value,mask=mask,dropout=self.dropout)
        
        #通过多头注意力计算后，得到了每个头计算结果组成的4维张量，我们需要将其转换为输入的形状
        #因此这里开始进行第一步处理环节的逆操作，先对第二和第三维进行转置，然后使用contiguous
        #这个方法的作用就是能够让转置后的张量应用view方法，否则将无法直接使用，
        #所以，下一步就是使用view重塑形状，变成和输入形状相同.
        x = x.transpose(1,2).contiguous().view(batch_size,-1,self.head*self.d_k)
        
        #最后使用线性层列表中的最后一个线性层对输入进行线性变换得到最终的多头注意力结构的输出.
        return self.linears[-1](x)

        

head = 8
embedding_dim=512
dropout=0.2
query = key = value = pe_result
mask = Variable(torch.zeros(2,4,4))
mha = MultiHeadAttention( head, embedding_dim, dropout)
mha_result = mha(query, key, value,mask)
print(mha_result)
print(mha_result.shape)