第十四章聚类方法.14.3K均值聚类

本课程来自深度之眼，部分截图来自课程视频以及李航老师的《统计学习方法》第二版。
公式输入请参考： 在线Latex公式

主要内容

k均值聚类的定义：类的中⼼、硬聚类
样本空间划分：特征向量、类与簇、从样本到类的函数
k均值聚类策略：损失函数最⼩化
损失函数的定义：各类损失函数的表达式与异同点
聚类算法总结：迭代算法、新类中⼼、收敛
k均值聚类实例：运⽤算法逐步求解聚类过程
k均值聚类算法特性：收敛性、初始类的选择、类别数k的选择
k均值聚类工作框架与改进：k均值算法流程与缺点改进方法

k均值聚类的定义

k均值聚类是基于样本集合划分的聚类算法。
k均值聚类将样本集合划分为k个⼦集，构成k个类，将n个样本分到k个类中，每个样本到其所属类的中⼼的距离最小。
每个样本只能属于⼀个类，k均值聚类是硬聚类。

样本空间划分

给定n个样本的集合
每个样本由⼀个特征向量表示，特征向量的维数是m。
k均值聚类的⽬标是将n个样本分到k个不同的类或簇中，这⾥假设$k＜n$。
k个类$G_1,G_2,\dots ,G_k$形成对样本集合X的划分，划分结果满足子空间互不相交：
$$G_i\cap G_j=\varnothing$$
且每个样本都属于某一个类：
$$\bigcup _{i=1}^k{G}_i=X$$
⽤C表示划分，⼀个划分对应着⼀个聚类结果。
划分C是⼀个多对⼀的函数，因为不同的划分获得的损失函数值可能一样。
k均值聚类的模型是⼀个从样本到类的函数。
划分或者聚类可以⽤函数$l=C_{(j)}$表示，其中样本⽤⼀个整数$i\in \{1,2,\cdots ,n\}$表示，类⽤⼀个整数$l\in \{1,2,\cdots ,k\}$表示。

k均值聚类策略

k均值聚类归结为样本集合X的划分，或者从样本到类的函数的选择问题。
k均值聚类的策略是通过损失函数的最⼩化选取最优的划分或函数$C^{\ast }$。
k均值聚类采⽤欧⽒距离平⽅（squared Euclidean distance）作为样本之间的距离 $d(x_i,x_j)$
$$d(x_i,x_j)=\sum _{k=1}^m(x_{ki}-x_{kj}{)}^2=||x_i-x_j|{|}^2$$
然后，定义样本与其所属类的中⼼之间的距离的总和为损失函数，即
$$W(C)=\sum _{l=1}^k\sum _{C(i)=l}||x_i-{\bar{x}}_l|{|}^2$$
内层求和是求各个样本点到该类中心的偏离程度求和，外层求和是各个类的偏离程度求和。
${\bar{x}}_l=({\bar{x}}_{1l},{\bar{x}}_{2l},\cdots ,{\bar{x}}_{ml}{)}^T$是第l个类的均值或中⼼，$n_l={\sum }_{i=1}^{n}I(C(i)=l)$
$I(C(i)=l)$是指示函数，取值1或0
$W(C)$函数也称为能量函数， 表示相同类中的样本相似的程度，我们希望$W(C)$越小越好。

k均值聚类就是求解最优化问题：
$$C^{\ast }=arg\underset{C}{\min }W(C)=arg\underset{C}{\min }\sum _{l=1}^k\sum _{C(i)=l}||x_i-{\bar{x}}_l|{|}^2$$

相似的样本被聚到同类时，损失函数值最⼩，这个⽬标函数的最优化能达到聚类的⽬的。
但是，这是⼀个组合优化问题，n个样本分到k类，所有可能分法的数⽬是：
$$S(n,k)=\frac{1}{k!}\sum _{l=1}^k(-1{)}^{k-1}{(}_l^k)k^n$$
事实上，k均值聚类的最优解求解问题是NP困难问题。现实中采⽤迭代的⽅法求解。归纳表达式为：
$$S(n,k)=S(n-1,k-1)+kS(n-1,k)$$

算法步骤

k均值聚类的算法是⼀个迭代的过程，每次迭代包括两个步骤。
⾸先选择k个类的中⼼，将样本逐个指派到与其最近的中⼼的类中，得到⼀个聚类结果
然后更新每个类的样本的均值，作为类的新的中心。
重复以上步骤，直到收敛为止。
收敛条件就是新的中心和上一步的中心不能离得太远，要小于一个常数：
$$|{\bar{x}}_l^{(k)}-{\bar{x}}_l^{(k+1)}|<\epsilon$$

更具体一点：
⾸先，对于给定的中心值$(m_1,m_2,\cdots ,m_k)$，求⼀个划分C，使得⽬标函数极⼩化：
$$\underset{C}{\min }\sum _{l=1}^k\sum _{C(i)=l}||x_i-m_l|{|}^2$$
就是说在类中⼼确定的情况下，将每个样本分到⼀个类中，使样本和其所属
类的中⼼之间的距离总和最⼩。
求解结果，将每个样本指派到与其最近的中⼼$m_l$的类$G_l$中。
然后，对给定的划分C，再求各个类的中⼼$(m_1,m_2,\cdots ,m_k)$，使得⽬标函数极⼩化：
$$\underset{m_1,m_2,\cdots ,m_k}{\min }\sum _{l=1}^k\sum _{C(i)=l}||x_i-m_l|{|}^2$$
就是说在划分确定的情况下，使样本和其所属类的中⼼之间的距离总和最⼩
求解结果，对于每个包含$n_l$个样本的类$G_l$，更新其均值$m_l$
$$m_l=\frac{1}{n_l}\sum _{C(i)=l}{x}_i,l=1,2,\cdots ,k$$
重复以上两个步骤， 直到划分不再改变，得到聚类结果
k均值聚类算法的复杂度是$O(mnk)$，其中m是样本维数，n是样本个数，k是类别个数。

例题

给定含有5个样本的集合
$$X=\left[\begin{array}{ccccc}0& 0& 1& 5& 5\\ 2& 0& 0& 0& 2\end{array}\right]$$
试⽤k均值聚类算法将样本聚到2个类中。
1.要把样本分为两类，先选择第一个和第二个样本作为类的中心
2.其他三个样本到这两个类中心的距离分布为：

样本到中心的距离	第一类	第二类	归属
第三个样本	5	1	第二类
第四个样本	29	25	第二类
第五个样本	25	29	第一类

3.得到新的类：$G_1^{(1)}=\{x_1,x_5\},G_2^{(1)}=\{x_2,x_3，x_4\}$，重新计算两个类的中心点（相同维度累加除以样本个数）：
$$m_1^{(1)}=(2.5,2{)}^T,m_2^{(1)}=(2,0{)}^T$$
4.重复步骤2和3
2.计算样本到中心的距离

样本到中心的距离	第一类	第二类	归属
第一个样本	6.25	16	第一类
第二个样本	10.25	4	第二类
第三个样本	6.25	1	第二类
第四个样本	10.25	9	第二类
第五个样本	10.25	13	第一类

得到新的类：$G_1^{(2)}=\{x_1,x_5\},G_2^{(2)}=\{x_2,x_3，x_4\}$
由于得到的新的类没有改变，聚类停止。得到聚类结果：
$$G_1^{\ast }=\{x_1,x_5\},G_2^{\ast }=\{x_2,x_3，x_4\}$$
这里注意，如果初始中心点选择的样本不同，得到的结果不一样。

k均值聚类算法特性

总体特点
• 基于划分的聚类⽅法，划分方法C不同，结果不同
• 类别数k事先指定，这个是一个缺点，后面会讲如何缺点k
• 以欧⽒距离平⽅表示样本之间的距离，以中⼼或样本的均值表示类别
• 以样本和其所属类的中⼼之间的距离的总和为最优化的⽬标函数
• 得到的类别是平坦的、⾮层次化的
• 算法是迭代算法，不能保证得到全局最优。

收敛性

k均值聚类属于启发式⽅法，不能保证收敛到全局最优，初始中⼼的选择会直接影响聚类结果。
注意，类中⼼在聚类的过程中会发⽣移动，但是往往不会移动太⼤，因为在每⼀步，样本被分到与其最近的中⼼的类中。

初始类的选择

选择不同的初始中⼼，会得到不同的聚类结果。
初始中⼼的选择，⽐如可以⽤层次聚类对样本进⾏聚类，得到k个类时停⽌。
然后从每个类中选取⼀个与中⼼距离最近的点。
还可以有轮廓系数法，具体看https://www.jianshu.com/p/335b376174d4

类别数k的选择

k均值聚类中的类别数k值需要预先指定，⽽在实际应⽤中最优的k值是不知道的。
尝试⽤不同的k值聚类，检验得到聚类结果的质量，推测最优的k值。
聚类结果的质量可以⽤类的平均直径来衡量。
⼀般地，类别数变⼩时，平均直径会增加
类别数变⼤超过某个值以后，平均直径会不变，⽽这个值正是最优的k值。
实验时，可以采⽤⼆分查找，快速找到最优的k值。

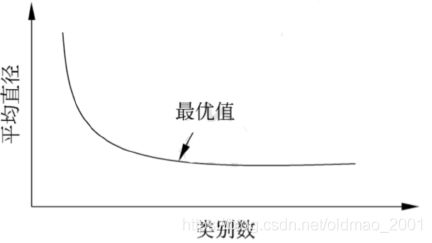
根据类别数取算SSE，得到曲线，找到SSE下降的转折点，就是我们要求的k值。

k均值聚类缺点改进

缺点a：需事先给出待⽣成簇的数⽬k，⽽此k不⼀定是使得损失函数极⼩化
的最佳值。
改进：肘部算法，属于启发式算法，⽤以估计最优聚类数量，也称肘部法则
(Elbow Method)。
缺点b：需借助随机种⼦⽣成起点，若起点不同，可能导致算法陷⼊局部最
优化。
改进：k-means++算法，初始聚类中⼼相互间距离尽可能远。