基于PaddlePaddle框架对CIFAR-100数据集在简易CNN（LeNet-5修改）和简易DNN的效果对比

CIFAR-100数据集在简易CNN（LeNet-5修改）和简易DNN的效果对比

项目说明

该项目为课程作业，实验过程等没有非常严谨，如有问题请指正，会及时改正！

摘要

本文对相同数据集使用简易线性神经网络和卷积神经网络进行探究，分别使用3层线性网络和LeNet-5的修改版本（通道数修改）进行训练并对数据情况进行分析。通过实验探究简易卷积网络和线性网络在相同数据集下的训练效果和情况，初步探究训练，简易CNN和DNN模型在该数据集的作用及意义。

关键词

神经网络，CIFAR-100，CNN，DNN

引言

在人工智能技术盛行的今天，在cv（计算机视觉）领域各种效果极佳的模型纷纷踊跃，回顾发展历史卷积网络的提出有着不可忽视的意义和作用，为了探究相同数据集在简易卷积神经网络和线性神经网络之间的效果差异，进行下列实验，通过数据集引入，数据处理，模型构建，模型训练，训练结果可视化等方式对数据效果进行展示，通Loss和ACC对模型效果进行简易判断。

import paddle
import numpy as np
import matplotlib.pyplot as plt
import paddle.nn as nn
from paddle.vision.datasets import Cifar100
from paddle.vision.transforms import Normalize

paddle.__version__

'2.3.0'

数据说明

CIFAR-100 数据集由 100 个类别的 60000 个 32x32 彩色图像组成，每个类别包含 6000 个图像。有 500 个训练图像和 100 个测试图像。CIFAR-100 中的 100 个类分为 20 个超类。每个图像都带有一个“精细”标签（它所属的类）和一个“粗略”标签（它所属的超类）。

超类	课程
水生哺乳动物	海狸, 海豚, 水獭, 海豹, 鲸鱼
鱼	观赏鱼, 比目鱼, 射线, 鲨鱼, 鳟鱼
花卉	兰花、罂粟、玫瑰、向日葵、郁金香
食品容器	瓶、碗、罐、杯、盘
水果和蔬菜	苹果、蘑菇、橙子、梨、甜椒
家用电器	时钟, 电脑键盘, 灯, 电话, 电视
家居家具	床, 椅子, 沙发, 桌子, 衣柜
昆虫	蜜蜂, 甲虫, 蝴蝶, 毛毛虫, 蟑螂
大型食肉动物	熊, 豹, 狮子, 虎, 狼
大型人造户外物品	桥, 城堡, 屋, 路, 摩天大楼
大型自然户外场景	云, 森林, 山, 平原, 海
大型杂食动物和草食动物	骆驼, 牛, 黑猩猩, 大象, 袋鼠
中型哺乳动物	狐狸、豪猪、负鼠、浣熊、臭鼬
非昆虫无脊椎动物	螃蟹、龙虾、蜗牛、蜘蛛、蠕虫
人们	宝贝, 男孩, 女孩, 男人, 女人
爬行动物	鳄鱼, 恐龙, 蜥蜴, 蛇, 龟
小型哺乳动物	仓鼠, 老鼠, 兔子, 鼩鼱, 松鼠
树木	枫木, 橡木, 棕榈, 松树, 柳树
车辆 1	自行车, 公共汽车, 摩托车, 皮卡车, 火车
车辆 2	割草机, 火箭, 有轨电车, 坦克, 拖拉机

参考地址：https://www.cs.toronto.edu/~kriz/cifar.html

数据导入

# 数据预处理定义
normalize = Normalize(mean=[0.5, 0.5, 0.5],
                        std=[0.5, 0.5, 0.5],
                        data_format='HWC')

# 训练集和验证集定义
train_cifar100 = Cifar100(mode='train', transform=normalize)
test_cifar100 = Cifar100(mode='test', transform=normalize)

构造数据并修改shape

数据的形状为（32,32,3）里面的通道和平时经常使用的方式不一样所以通过paddle.io.dataset重新进行构造使得数据变成（3,32,32）的样式

'''
自定义数据集
'''
from paddle.io import Dataset
class MyDataset(paddle.io.Dataset):
    """
    步骤一：继承paddle.io.Dataset类
    """
    def __init__(self, data_):
        """
        步骤二：实现构造函数，定义数据集大小
        """
        super(MyDataset, self).__init__()
        self.data = []
        self.label = []
        for i in range(len(data_)):
            x = data_[i][0].transpose((2, 0, 1))
            y = data_[i][1]

            self.data.append(x)
            self.label.append(np.array(y).astype('int64'))
        
    def __getitem__(self, index):
        """
        步骤三：实现__getitem__方法，定义指定index时如何获取数据，并返回单条数据（训练数据，对应的标签）
        """
        # 返回单一数据和标签
        data = self.data[index]
        label = self.label[index]
        # 注：返回标签数据时必须是int64
        return data, np.array(label, dtype='int64')
    def __len__(self):
        """
        步骤四：实现__len__方法，返回数据集总数目
        """
        # 返回数据总数
        return len(self.data)

# 测试定义的数据集
train_dataset = MyDataset(data_=train_cifar100)
eval_dataset = MyDataset(data_=test_cifar100)
print('=============train_dataset =============')
# 输出数据集的形状和标签
print(train_dataset.__getitem__(1)[0].shape,train_dataset.__getitem__(1)[1])
# 输出数据集的长度
print(train_dataset.__len__())
print('=============eval_dataset =============')
# 输出数据集的形状和标签
for data, label in eval_dataset:
    print(data.shape, label)
    break
# 输出数据集的长度
print(eval_dataset.__len__())

DNN网络（深度神经网络）

DNN属于第3代神经网络，一般意义上大于两层的线性网络属于DNN。DNN有时也叫做多层感知机（Multi-Layer perceptron,MLP）

DNN是一种最简单的神经网络。各个神经元分别属于不同的层，每个神经元和前一层的所有神经元相连接，信号从输入层向输出层单向传播。

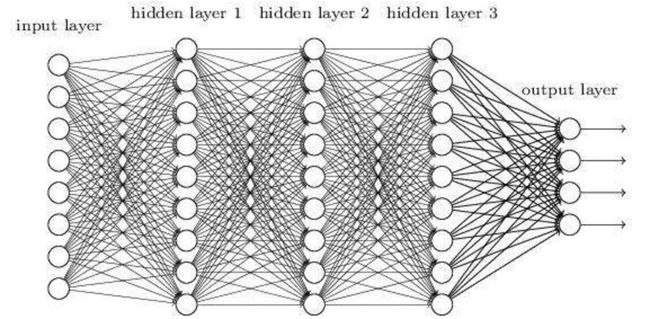
从DNN按不同层的位置划分，DNN内部的神经网络层可以分为三类，输入层，隐藏层和输出层,如下图示例，一般来说第一层是输入层，最后一层是输出层，而中间的层数都是隐藏层。

层与层之间是全连接的，也就是说，第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。虽然DNN看起来很复杂，但是从小的局部模型来说，还是和感知机一样，即一个线性关系 加上一个激活函数。

简单来说就是一个输入层加上隐藏层加上输出层构成的简易神经网络。隐藏层的深度在一定程度上决定模型的复杂度和效果。

DNN模型的构建

from paddle.nn import Linear
import paddle.nn.functional as F
import paddle

# 定义DNN网络
class MyDNN(paddle.nn.Layer):
    def __init__(self):
        super(MyDNN, self).__init__()
        self.hidden1 = Linear(3*32*32, 2048)  # 输入层定义
        self.hidden2 = Linear(2048, 1024)  # 隐藏层1定义
        self.hidden3 = Linear(1024, 128)  # 隐藏层2定义
        self.hidden4 = Linear(128, 100)  # 输出层定义
    
    def forward(self, input):
        # print(input.shape)
        x = paddle.reshape(input, shape=[-1,3*32*32])  # 数据拉直
        x = self.hidden1(x)  # 输入层
        x =F.relu(x)  # 激活函数
        # print(x.shape)
        x = self.hidden2(x)  # 隐藏层1
        x = F.relu(x)
        # print(x.shape)
        x = self.hidden3(x)  # 隐藏层2
        x = F.relu(x)
        # print(x.shape)
        x = self.hidden4(x)  # 输出层
        y = F.softmax(x)
        # print(y.shape)
        return y

model = MyDNN()  # 网络实例化
paddle.summary(model,(3,32,32))  # 网络结构查看

---------------------------------------------------------------------------
 Layer (type)       Input Shape          Output Shape         Param #    
===========================================================================
   Linear-1         [[1, 3072]]           [1, 2048]          6,293,504   
   Linear-2         [[1, 2048]]           [1, 1024]          2,098,176   
   Linear-3         [[1, 1024]]            [1, 128]           131,200    
   Linear-4          [[1, 128]]            [1, 100]           12,900     
===========================================================================
Total params: 8,535,780
Trainable params: 8,535,780
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.01
Forward/backward pass size (MB): 0.03
Params size (MB): 32.56
Estimated Total Size (MB): 32.60
---------------------------------------------------------------------------

{'total_params': 8535780, 'trainable_params': 8535780}

使用DNN模型对数据进行训练

通过上面对模型的结构查看可以清楚看到，输入层为(1, 3072)就是(3, 32, 32)数据拉平。隐藏层为两层的线性结构。输出层为100个输出的输出层。

对吗，模型进行训练，此处使用了Adam优化器，能够利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。其参数更新的计算公式如下：

参考文献：Adam: A Method for Stochastic Optimization https://arxiv.org/abs/1412.6980

损失函数：使用的是CrossEntropyLoss，用于计算输入input和标签label间的交叉熵损失 ，它结合了 LogSoftmax 和 NLLLoss 的计算，适用于训练一个 n 类分类器。

评估指标：使用的是Accuracy，用于计算准确率。

根据训练轮数50轮，批次128，打乱样本进行训练。

# 用Model封装模型
model = paddle.Model(MyDNN())
# 定义损失函数
model.prepare(paddle.optimizer.Adam(parameters=model.parameters()),
              paddle.nn.CrossEntropyLoss(),
              paddle.metric.Accuracy(topk=(1,5)))

# 训练可视化VisualDL工具的回调函数
visualdl = paddle.callbacks.VisualDL(log_dir='visualdl_log')

# 启动模型全流程训练
model.fit(train_dataset,            # 训练数据集
          eval_dataset,            # 评估数据集
          epochs=50,            # 总的训练轮次
          batch_size = 128,    # 批次计算的样本量大小
          shuffle=True,             # 是否打乱样本集
          verbose=1,                # 日志展示格式
          save_dir='./chk_points/', # 分阶段的训练模型存储路径
          callbacks=[visualdl])     # 回调函数使用
          
# 保存模型
model.save('model_save_dir')

训练数据可视化

通过把训练数据进行可视化展示可以得到以下数据

DNN数据信息

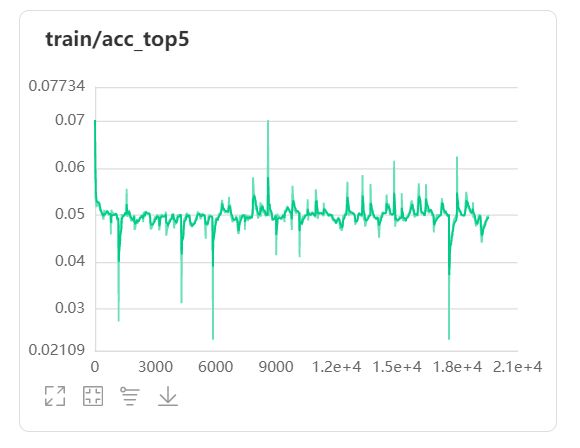
通过训练数据可以看出来测试集里面loss比较稳定，acc存在一定的波动，但是loss值偏高，ACC偏低，可以看出效果较差。通过loss的稳定可以看出来在一定程度上该模型已经达到一种饱和程度，模型复杂的和深度不足以支持该任务的训练。

CNN

CNN是一种通过卷积计算的前馈神经网络，其是受生物学上的感受野机制提出的，具有平移不变性，使用卷积核，最大的应用了局部信息，保留了平面结构信息。

使用反向传播算法训练的多层神经网络构成了成功的基于梯度的学习技术，给定适当的网络架构，基于梯度的学习算法可用于合成复杂的决策面，该决策面可以对手写字符等高维模式进行分类，且预处理最少。卷积神经网络专门设计用于处理 2D 形状的可变性，其性能优于当时的所有其他技术。（该技术为1998年的技术，不是最新成果）。主要使用的是LeNet-5在手写数字识别（http://yann.lecun.com/exdb/mnist/ ）项目上的，在当时有着比较好的效果。

LeNet-5

LeNet-5是基础卷积神经网络

是从原始信号—>发现边缘和方向—>不断抽象—>不断抽象的一个过程

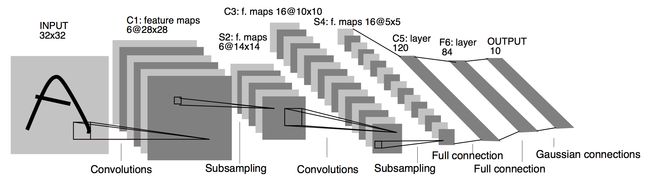
LeNet-5由输入层，两个卷积层两个平均池化层组成，后面接了两个线性层还有一个输出层。

具体今天常考下面的图及原论文。

参考地址：https://ieeexplore.ieee.org/document/726791

论文地址（直接可读）：https://arxiv.org/abs/1412.6980

[1] Y. Lecun, L. Bottou, Y. Bengio and P. Haffner, “Gradient-based learning applied to document recognition,” in Proceedings of the IEEE, vol. 86, no. 11, pp. 2278-2324, Nov. 1998, doi: 10.1109/5.726791.

卷积、池化和激活函数说明

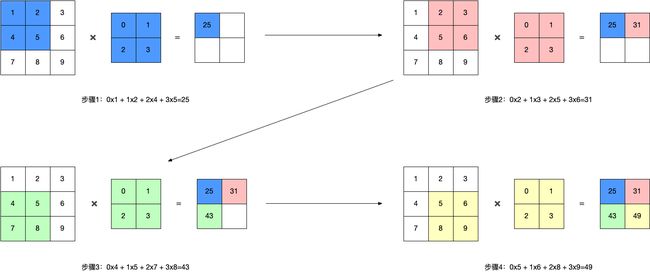
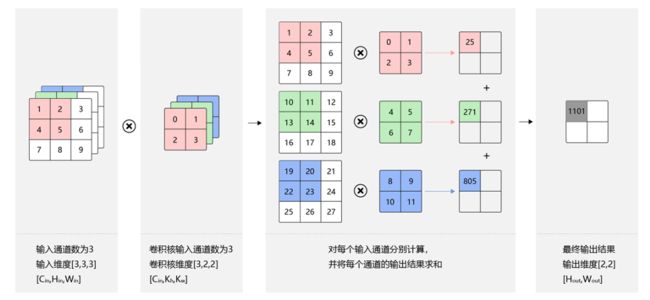
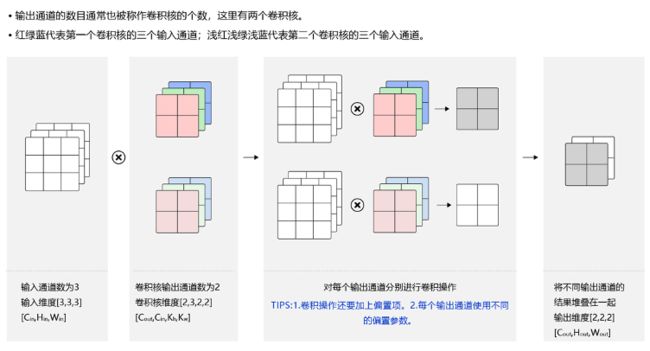
卷积

每个卷积单元的参数都是通过反向传播算法最佳化得到的。卷积运算的目的是提取输入的不同特征，第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级，更多层的网路能从低级特征中迭代提取更复杂的特征。

• 单层卷积：
  输入数据在和卷积核在指定做卷积操作。然后生成新的具有具体特征的新数据
  

• 多层卷积：

和单层卷积相同，但是生成新的数据也是多层的数据

• 填充（Padding）

角落边缘的像素，只被一个过滤器输出所使用，因为它位于这个3×3的区域的一角。但如果是在中间的像素点，就会有许多3×3的区域与之重叠。
所以那些在角落或者边缘区域的像素点在输出中采用较少，意味着你丢掉了图像边缘位置的许多信息。
那么出现的一个解决办法就是填充操作，在原图像外围以0进行填充，在不影响特征提取的同时，增加了对边缘信息的特征提取。
另外一个好处是，我们在做卷积操作时，每经过一次卷积我们的输入图像大小就会变小，最后经过多次卷积可能我们的图像会变得特别小，我们不希望图像变小的话就可以通过填充操作。

池化

池化是使用某一位置的相邻输出的总体统计特征代替网络在该位置的输出，其好处是当输入数据做出少量平移时，经过池化函数后的大多数输出还能保持不变。比如：当识别一张图像是否是人脸时，我们需要知道人脸左边有一只眼睛，右边也有一只眼睛，而不需要知道眼睛的精确位置，这时候通过池化某一片区域的像素点来得到总体统计特征会显得很有用。由于池化之后特征图会变得更小，如果后面连接的是全连接层，能有效的减小神经元的个数，节省存储空间并提高计算效率。

池化的作用

池化层是特征选择和信息过滤的过程，过程中会损失一部分信息，但是会同时会减少参数和计算量，在模型效果和计算性能之间寻找平衡，随着运算速度的不断提高，慢慢可能会有一些设计上的变化，现在有些网络已经开始少用或者不用池化层。

池化的步长和卷积核的大小有关，默认长度为2

平均池化(Avg Pooling)

对邻域内特征点求平均

• 优缺点：能很好的保留背景，但容易使得图片变模糊
• 正向传播：邻域内取平均
• 反向传播：特征值根据领域大小被平均，然后传给每个索引位置

最大池化(Max Pooling)

对邻域内特征点取最大

• 优缺点：能很好的保留一些关键的纹理特征，现在更多的再使用Max Pooling而很少用Avg Pooling
• 正向传播：取邻域内最大，并记住最大值的索引位置，以方便反向传播
• 反向传播：将特征值填充到正向传播中，值最大的索引位置，其他位置补0

计算结果的大小公示

激活函数

• Sigmoid

• Tanh

Sigmoid和Tanh激活函数有共同的缺点：即在z很大或很小时，梯度几乎为零，因此使用梯度下降优化算法更新网络很慢。

• ReLU

Relu目前是选用比较多的激活函数，但是也存在一些缺点，在z小于0时，斜率即导数为0。

为了解决这个问题，后来也提出来了Leaky Relu激活函数，不过目前使用的不是特别多。

• 注此处使用的是Tanh激活函数

LeNet-5模型搭建

# LeNet-5
network = nn.Sequential(
    nn.Conv2D(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=0),  # C1 卷积层
    nn.Tanh(),
    nn.AvgPool2D(kernel_size=2, stride=2),  # S2 平局池化层
    nn.Sigmoid(),   # Sigmoid激活函数
    nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0),  # C3 卷积层
    nn.Tanh(),
    nn.AvgPool2D(kernel_size=2, stride=2),  # S4 平均池化层
    nn.Sigmoid(),  # Sigmoid激活函数
    nn.Conv2D(in_channels=16, out_channels=120, kernel_size=5, stride=1, padding=0), # C5 卷积层
    nn.Tanh(),
    nn.Flatten(),
    nn.Linear(in_features=120, out_features=84), # F6 全连接层
    nn.Tanh(),
    nn.Linear(in_features=84, out_features=10) # OUTPUT 全连接层
)

paddle.summary(network, (1, 1, 32, 32))

模型修改为3层

# LeNet-5改
network = nn.Sequential(
    nn.Conv2D(in_channels=3, out_channels=6, kernel_size=5, stride=1, padding=0),  # C1 卷积层
    nn.Tanh(),
    nn.AvgPool2D(kernel_size=2, stride=2),  # S2 平局池化层
    nn.Sigmoid(),   # Sigmoid激活函数
    nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0),  # C3 卷积层
    nn.Tanh(),
    nn.AvgPool2D(kernel_size=2, stride=2),  # S4 平均池化层
    nn.Sigmoid(),  # Sigmoid激活函数
    nn.Conv2D(in_channels=16, out_channels=120, kernel_size=5, stride=1, padding=0), # C5 卷积层
    nn.Tanh(),
    nn.Flatten(),
    nn.Linear(in_features=120, out_features=100), # F6 全连接层
    nn.Tanh(),
    nn.Linear(in_features=100, out_features=100) # OUTPUT 全连接层
)

paddle.summary(network, (1, 3, 32, 32))

基于最新的构造函数进行改写

对paddle.nn.Layer进行继承，函数和向前计算网络进行分开书写，更加方便对网络的了解和对问题的查看

class LeNet_G(nn.Layer):
    """
    继承paddle.nn.Layer定义网络结构
    """

    def __init__(self, num_classes=100):
        """
        初始化函数
        """
        super(LeNet_G, self).__init__()
        self.conv2D1 = nn.Conv2D(in_channels=3, out_channels=6, kernel_size=5, stride=1, padding=0)  # C1 卷积层
        self.conv2D2 = nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0)  # C3 卷积层
        self.conv2D3 = nn.Conv2D(in_channels=16, out_channels=120, kernel_size=5, stride=1, padding=0)  # C5 卷积层
        self.avgpool2D1 = nn.AvgPool2D(kernel_size=2, stride=2)  # S2平均池化
        self.avgpool2D2 = nn.AvgPool2D(kernel_size=2, stride=2)  # S4 平均池化层
        self.sigmoid = nn.Sigmoid()  # 激活函数
        self.tanh = nn.Tanh()
        self.linear1 = nn.Linear(in_features=120, out_features=100)  # F6 全连接层
        self.linear2 = nn.Linear(in_features=100, out_features=num_classes) # OUTPUT 全连接层


    def forward(self, inputs):
        """
        前向计算
        """
        inputs = paddle.to_tensor(inputs)
        x = self.conv2D1(inputs)
        x = self.tanh(x)
        x = self.avgpool2D1(x)
        x = self.sigmoid(x)
        x = self.conv2D2(x)
        x = self.tanh(x)
        x = self.avgpool2D2(x)
        x = self.sigmoid(x)
        x = self.conv2D3(x)
        x = self.tanh(x)
        x = paddle.flatten(x, 1)
        x = self.linear1(x)
        x = self.tanh(x)
        y = self.linear2(x)
        return x

network_1 = LeNet_G()
paddle.summary(network_1, (1, 3, 32, 32))

---------------------------------------------------------------------------
 Layer (type)       Input Shape          Output Shape         Param #    
===========================================================================
   Conv2D-1       [[1, 3, 32, 32]]      [1, 6, 28, 28]          456      
    Tanh-1           [[1, 100]]            [1, 100]              0       
  AvgPool2D-1     [[1, 6, 28, 28]]      [1, 6, 14, 14]           0       
   Sigmoid-1      [[1, 16, 5, 5]]       [1, 16, 5, 5]            0       
   Conv2D-2       [[1, 6, 14, 14]]     [1, 16, 10, 10]         2,416     
  AvgPool2D-2    [[1, 16, 10, 10]]      [1, 16, 5, 5]            0       
   Conv2D-3       [[1, 16, 5, 5]]       [1, 120, 1, 1]        48,120     
   Linear-1          [[1, 120]]            [1, 100]           12,100     
   Linear-2          [[1, 100]]            [1, 100]           10,100     
===========================================================================
Total params: 73,192
Trainable params: 73,192
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.01
Forward/backward pass size (MB): 0.07
Params size (MB): 0.28
Estimated Total Size (MB): 0.36
---------------------------------------------------------------------------

{'total_params': 73192, 'trainable_params': 73192}

基于模型进行训练

# 用Model封装模型
model = paddle.Model(network_1)
# 定义损失函数
model.prepare(paddle.optimizer.Adam(learning_rate=0.0001, parameters=model.parameters()), 
              paddle.nn.CrossEntropyLoss(), 
              paddle.metric.Accuracy())

# 训练可视化VisualDL工具的回调函数
visualdl = paddle.callbacks.VisualDL(log_dir='visualdl_log')

# 启动模型全流程训练
model.fit(train_dataset,            # 训练数据集
          eval_dataset,            # 评估数据集
          epochs=50,            # 总的训练轮次
          batch_size = 256,    # 批次计算的样本量大小
          shuffle=True,             # 是否打乱样本集
          verbose=1,                # 日志展示格式
          save_dir='./CNN_points/', # 分阶段的训练模型存储路径
          callbacks=[visualdl])     # 回调函数使用
          
# 保存模型
  shuffle=True,             # 是否打乱样本集
          verbose=1,                # 日志展示格式
          save_dir='./CNN_points/', # 分阶段的训练模型存储路径
          callbacks=[visualdl])     # 回调函数使用
          
# 保存模型
model.save('cnn_model_save_dir')

训练数据可视化

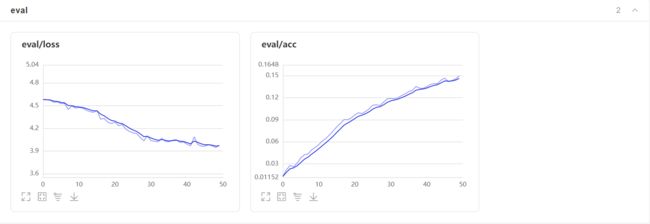
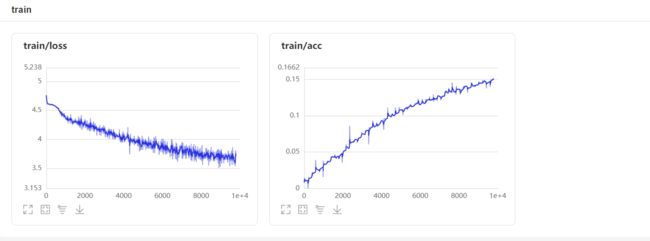
CNN训练信息

通过训练集和测试集可以明显看出loss处于波动下降的状态，可以看出“学习”是具有成效的，通过ACC逐步上升也可以证明训练的结果是有成效的。但是就训练的数据来看，效果极差，主要原因可能基于以下几个方面：

1、数据种类较多，但是单个样本的数据量并不足够

2、模型较为简单，复杂的和深度都不够

3、训练轮数，学习率等参数还可以进行修正和调整

在当前结果下可以看出该模型是有一定效果的，但是在当前的参数和数据下效果不明显，还有较大的提升空间。

总结

通过卷积和线性神经网络对图像的分类任务看来，简单的线性效果没有简单的卷积好，而且简单的线性网络提升空间已经没有了，到达极限，只能够通过加深网络等其他的方式进行，在相同轮数的训练下，卷积网络还有较大的提升空间。在一定程度上可以得到结论在对图像分类的项目上简单线性网络效果没有简单的卷积好，而且在50轮的一个训练轮数下，简单线性网络已经达到了学习极值，上升空间小，而简单的卷积网络在不改变网络复杂的和深度的前提下，还有较大的提升空间，例如：增加训练轮数，修改学习率等参数，还有较大提升空间。

通过本实验一定程度上了解了简单的DNN网络（3层）和CNN网络（变形的LeNet-5网络，修改成了3通道）在学习率为：0.001，损失函数为交叉熵（cross entropy）（CrossEntropyLoss），评估指标为Accuracy的前提下，对图像进行分类处理（CV分类任务），通过50轮的训练得到了效果，通过效果得出结论，简易CNN在对图像分类任务上的效果好于简易DNN，且在该条件下CNN还有进一步学习和优化的空间。

卷积神经网络在对图像的特征信息提取上具有不可磨灭的优势，且在近些年的各类研究成果中也不断证明卷积的作用是有效的。

作者简介

作者：三岁
经历：自学python，现在混迹于paddle社区，希望和大家一起从基础走起，一起学习Paddle
csdn地址：https://blog.csdn.net/weixin_45623093/article/list/3
我在AI Studio上获得至尊等级，点亮10个徽章，来互关呀~ https://aistudio.baidu.com/aistudio/personalcenter/thirdview/284366

传说中的飞桨社区最菜代码人，让我们一起努力！
记住：三岁出品必是精品 （不要脸系列）