TensorFlow之文本分类算法-3

1 前言

2 收集数据

3 探索数据

4 选择模型

5 准备数据

N-gram向量集

序列向量集

序列向量集主要是用于序列模型中对文本执行分词与向量化，与n-gram向量集类似，也使用特征选择与标准化的技术优化序列向量集的表示。

在一些文本样例中，单词的顺序会对文本的意义产生关键的影响，也就是，单词顺序不同，则文本表示的意义不同。例如，文本【I used to hate my commute. My new bike changed that completely】，只能在按单词的顺序理解文本自身的意义。模型CNNs/RNNs（卷积神经网络/循环神经网络，在后续章节中详细描述）能按照样例中单词的顺序推断出文本的意义。因此，对于这些模型，使用分词的序列表示文本，而序列会体现出分词在原文中的顺序。

分词

文本可以表示成一个字符序列或者一个单词序列，实际证明单词序列的表示能提供更加优越的性能，在工业界这是一种常用而且高效的文本处理方法，而字符序列只适用于存在大量拼写错误的文本中，这是非常少见的场景。

向量化

向量化是将分词所得的单词序列转换成数字化的向量集，使用1-gram以及分词索引实现向量化的转换如下所示：

如上所示，Texts是原文本，包括两个文本，Index表示使用1-gram分词所得的索引列表，列表中每个分词是乱序的，其编号表示的索引位是从1到6，而索引位0用于标识未知的分词，索引位1表示分词the，由于the在原文中出现的频率高，因此，其索引位被赋予值1。Sequence表示第一个文本的数字化的单词序列，序列是按照原文的单词顺序排列，其中1表示索引位的the，2表示索引位的mouse，以此类推。

以下分别描述两类单词序列的编码方式，One-hot encoding、Word embeddings。

One-hot encoding

该编码方式是使用n维向量空间表示单词序列，其中，n表示分词所得的词汇总量，如上例中，n等于7。由于以词汇为单位的表示方式简单，因此，其耗费的工作量也很小，但是在实际的应用场景中，词汇总量通常达到几十万个，one-hot编码方式将使得向量集合变得非常稀疏以及低效，如下所示：

如上所示，文本是二维数组，其中，第一维的大小等于6，表示原文单词序列的大小。第二维的大小等于7，表示单词序列中每个元素在词汇中的索引位。例如，第一维对应的第一行是[0, 1, 0, 0, 0, 0, 0]，对应词汇集合中的第一索引位的元素，表示the，第二维对应的第二行是[0, 0, 1, 0, 0, 0, 0]，对应词汇集合中的第二索引位的元素，表示mouse，依次类推。

Word embeddings

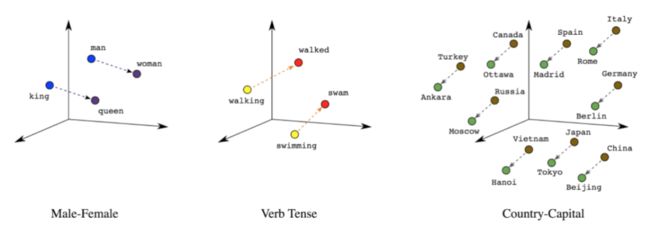
该编码方式是使用嵌入层处理相似的分词集合，使用一个稠密的向量空间表示分词集合，向量空间中的单词位置以及单词之间的距离可以体现出单词的相似度，其关系模型如下所示：

如上所示，Male-Female表示性别的向量空间，Verb Tense表示动词时态的向量空间，Country-Capital表示国家与首都的向量空间。

在神经网络的机器学习模型中，通常提供一个嵌入层作为第一层，该层的主要作用是将单词编码所得的向量集合转换成word embedding向量集合用于训练，其中，每个单词的索引都可以表示成一个稠密类型的向量集合，该向量集合存储真实的单词以及体现出单词在语义空间中的位置，嵌入层的演进如下所示：

如上所示，从左边向右边演进，左边输入原文，随后分词，根据分词的索引对原文编码，随后对编码的向量集合执行转换，每个单词对应一个稠密类型的表示。

特征选择

并非所有的分词在标签预测中都发挥作用，需要对机器学习的过程进行优化，使用有效的方法从词汇集合中删除那些出现频率较低或者与预测不相关的单词，如前面所述，事实证明选择20k的分词数据量作为特征分析与预测是最有效的，序列向量模型的执行步骤如下所示：

对文本执行分词 选择使用top-20k的词汇量 转换分词成序列向量集合 转换序列向量集合成固定的序列长度（稠密类型）

使用TensorFlow的技术框架实现代码步骤如下所示：

标签向量化

前面部分所描述内容是与原文的向量化相关，在实际的应用环境中，也需要将标签向量化，例如，可以将标签分类成[0, num_classes - 1]范围的数组，其中，num_classes是类别的总数。

稀疏矩阵的数据结构

在一个矩阵中，如果0值元素个数远大于非0值元素个数，则该矩阵是稀疏矩阵，为了节省存储空间，通常将稀疏矩阵进行压缩存储，其数据结构描述如下所示：

稀疏矩阵的压缩存储使用三个一维数组： 数组1：将矩阵中每列的非0值存储在该一维数组中，从矩阵的第一列开始递增排列 数组2：存储数组1中的每个元素在矩阵的行索引 数组3：存储数组1的索引位，每个元素表示数组2中开始矩阵新列的列索引，列索引递增，最后一个元素表示数组1的长度

假设，存在如下的矩阵： 1 0 0 2 3 0 数组1：[1,3,2] 数组2：[0,2,1] 数组3：[0,2,3]

稠密矩阵的数据结构

在一个矩阵中，如果0值元素个数远小于非0值元素个数，则该矩阵是稠密矩阵，其数据结构一般是直接使用一维数组存储，其数据结构描述如下所示：

稠密矩阵的存储使用一个一维数组： 数组1：将矩阵中每列的所有元素存储在该一维数组中，从矩阵的第一列开始递增排列

（未完待续）