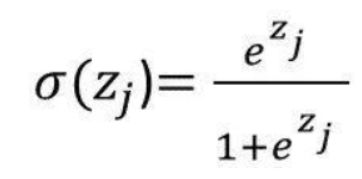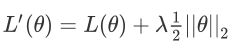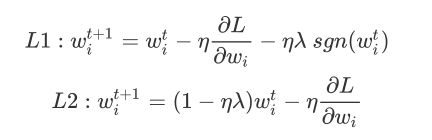独家思维导图!让你秒懂李宏毅2020深度学习(五)—— Tips for Deep Leaning & Why Deep?
独家思维导图!让你秒懂李宏毅2020深度学习(五)—— Tips for Deep Leaning & Why Deep?
系列文章传送门:
独家思维导图!让你秒懂李宏毅2020机器学习(一)—— Regression回归
独家思维导图!让你秒懂李宏毅2020机器学习(二)—— Classification分类
独家思维导图!让你秒懂李宏毅2020深度学习(三)—— 深度学习基础(神经网络和反向传播部分)
独家思维导图!让你秒懂李宏毅2020深度学习(四)—— CNN(Convolutional Neural network)
独家思维导图!让你秒懂李宏毅2020深度学习(五)—— Tips for Deep Leaning & Why Deep?
独家思维导图!让你秒懂李宏毅2020深度学习(六)—— Recurrent Neural Network(RNN)
文章目录
- 独家思维导图!让你秒懂李宏毅2020深度学习(五)—— Tips for Deep Leaning & Why Deep?
- Tips for Deep Leaning
-
- Do not always blame overfitting
-
- 总结:
- Good Results on Training Data?
-
- New activation function
-
- Vanishing Gradient Problem
-
- Why Vanishing Gradient?
- Activation Function Mindmap(干货!!!)
-
- ReLU
-
- Handle Vanishing gradient problem
- Adaptive learning rate
-
- Review - Adagrad
- RMSProp
-
- How to do RMSProp
- Momentum
-
- where is Momentum from
- how to do Momentum
- Adam
- Good Results on Testing Data?
-
- Early Stopping
- Regularization
-
- L2 regularization
- L1 regularization
- L1 V.s. L2
- Dropout(重要)
-
- How to do Dropout
-
- Training
- Testing
- Why Dropout?
- Dropout is a kind of ensemble
-
- 为什么dropout是⼀个终极的ensemble⽅法呢?
- 实际操作ensemble的做法
- Why Deep?
-
- Shallow V.s. Deep
-
- Deep is Better?
- Fat + Short v.s. Thin + Tall
- Modularization
-
-
- introduction
- example
- deep -> modularization
- 剪窗花(超级形象)
-
Tips for Deep Leaning
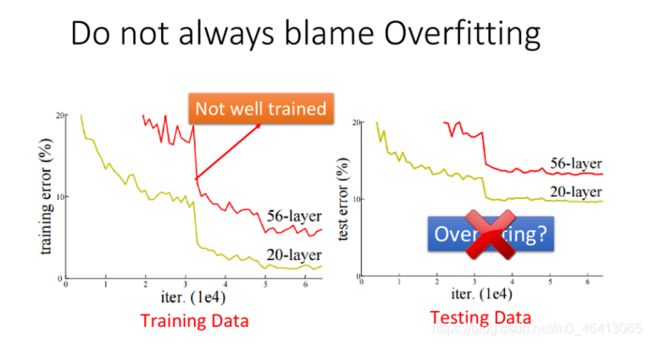
Do not always blame overfitting
不要看到所有不好的performance就归责于overfitting
【横坐标是model做gradient descent所update的次数,纵坐标则是error rate(越低说明model表现得越好)】
由右图可以看出在Testing Data中56层network的error rate⽐20层network的要高,也就是说20层比56层的performance要好,从而得出结论:56层的network参数太多以至于导致overfitting。但是,真的是这样⼦吗?
但是我们之前在regression中提到的overfitting是指在training data上,model越复杂,error就会越低;但是在testing data上,model复杂到⼀定程度之后,error⾮但不会减⼩,反⽽会暴增。
而现在的情况是在training set上20层的network本来就要⽐56层的network表现得更好,所以testing set得到的结果并不能说明56层的case就是发⽣了overfitting。
让training set表现的不好的因素有很多,⽐如有local minimum的问题,有saddle point的问题,有plateau的问题…所以这个56层的neural network,有可能在train的时候就卡在了⼀个local minimum的地⽅,于是得到了⼀个差的参数,但这并不是overfitting,⽽是在training的时候就没有train好。
当然,这个也不是underfitting,回顾我写的第一篇博客underfitting的本意应该是指这个model的complexity不⾜,这个model的参数不够多,所以它的能⼒不⾜以解出这个问题;但这个56层的network,它的参数是⽐20层的network要来得多的,有⽐20层的network要做的更好的能⼒,却没有得到理想的结果,这种情况不应该被称为underfitting,其实就只是没有train好⽽已。
总结:
deep learning中的方法无非是解决两种问题:
- 在training set上的performance不够好
- 在testing set上的performance不够好
因此我们要明确我们的问题到底是什么,然后再根据这个问题去找针对性的⽅法。
下⾯我们分别从Training data和Testing data两个问题出发,来讲述⼀些针对性优化的⽅法
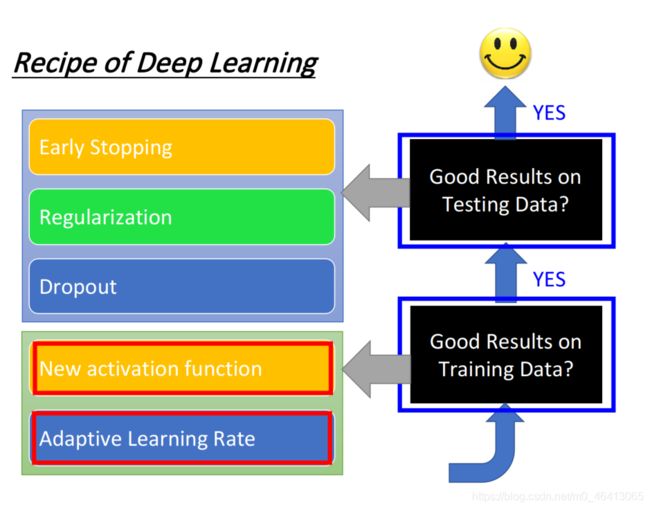
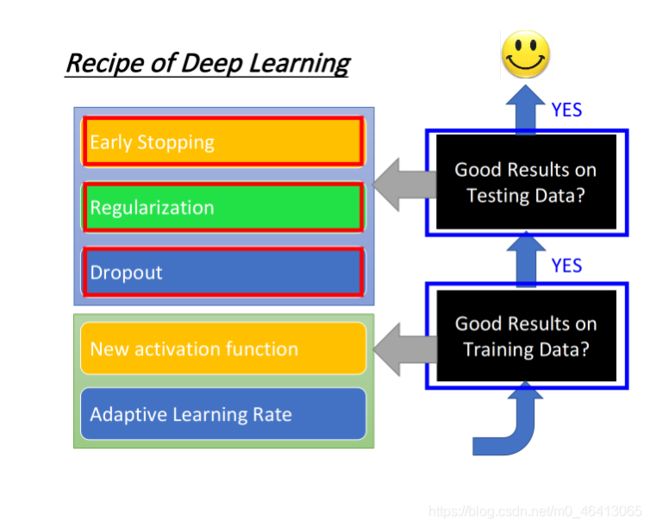
Good Results on Training Data?
这⼀部分主要讲述如何在Training data上得到更好的performance
分为两个模块
- New activation function
- Adaptive Learning Rate
New activation function
之前在我写的第三篇文章中我在讲神经网络的时候总结了最常见的几种activation function,当然也是按照解决问题,不断优化的顺序讲的,忘了的快回去补课:传送门
简单的解释下吧:
在1980年代,⽐较常⽤的activation function是sigmoid function,如果现在我们使⽤sigmoid function,你会发现deeper不⼀定imply better,下图是在MNIST⼿写数字识别上的结果,当layer越来越多的时候,accuracy⼀开始持平,后来就掉下去了,在layer是9层、10层的时候,整个结果就崩溃了;
但注意!9层、10层的情况并不能被认为是因为参数太多⽽导致overfitting,实际上这张图就只是training set的结果,你都不知道testing的情况,⼜哪来的overfitting之说呢?

Vanishing Gradient Problem
上⾯这个问题的原因不是overfitting,⽽是Vanishing Gradient(梯度消失),解释如下:
Why Vanishing Gradient?
我们知道,整个network的训练是通过gradient decent来不断进行update的,回顾我在第三章提到的Backpropagation,什么,又不记得了?回去补课传送门
回顾下整个Backpropagation流程:
让我们重点关注一下以下几个式子

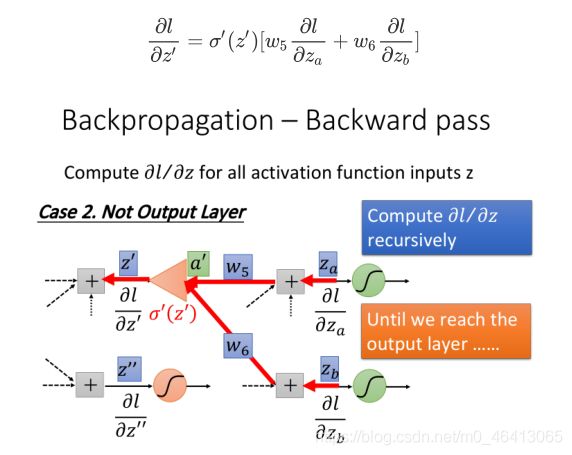
sigmoid函数的导数最大值为0.25
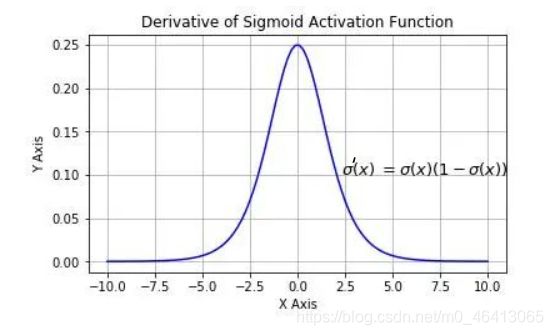
当把network叠得很深的时候,
在靠近input的地⽅,这些参数的gradient(即对最后loss function的微分)是⽐较⼩的;(乘了多层σ‘(z))
靠近output的地⽅,它对loss的微分值会是⽐较⼤的。
如果还觉得解释的不够清楚我再引用某篇博客中,以一个简单的每层单个神经元的神经网络为例子:
下面是一个输入层,三个隐藏层,一个输出层的简单神经网络。
通常abs(w)<1,所以可以得到下面的式子:
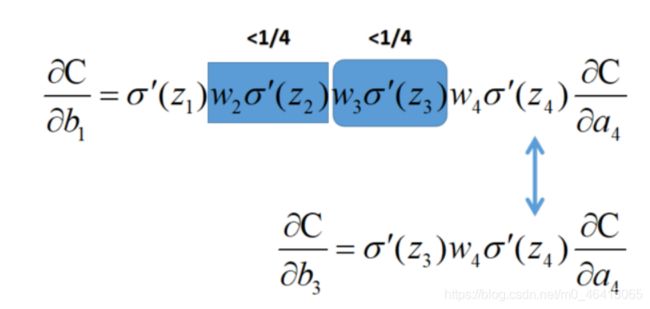
从上式中不难看出,随着网络层数加大,从前面的层传递到后面的层梯度会越来越小,进而引起了梯度消失的问题。
因此当你设定同样learning rate的时候,靠近input的地⽅,它参数的update是很慢的;⽽靠近output的地⽅,它参数的update是⽐较快的。
可以这么说,就是接近output的那些参数update比较快,能很快找到自己的local minima,但靠近input的地⽅,就算参数变化很大也很难对Loss函数造成影响,以至于update很慢。
所以在靠近input的地⽅,参数⼏乎还是random的时候,output就已经根据这些random的结果找到了⼀个local minima,然后就converge(收敛)了。这个时候你会发现,参数的loss下降的速度变得很慢,你就会觉得gradient已经接近于0了,于是把程序停掉了,由于这个converge,是⼏乎base on random的参数,所以model的参数并没有被训练充分, 那在training data上得到的结果肯定是很差的。
就算不看Backpropagation的式⼦,也可以理解梯度消失的原因
某⼀个参数w对total cost的偏微分,即gradient ∂ l ∂ w \frac{\partial l}{\partial w} ∂w∂l,意思是说,当我今天把这个参数做⼩⼩的变化的时候,它对这个cost的影响有多⼤;那我们就把第⼀个layer⾥的某⼀个参数w加上Δw,来看下w的改变对network的output和target之间的loss有什么样的影响。
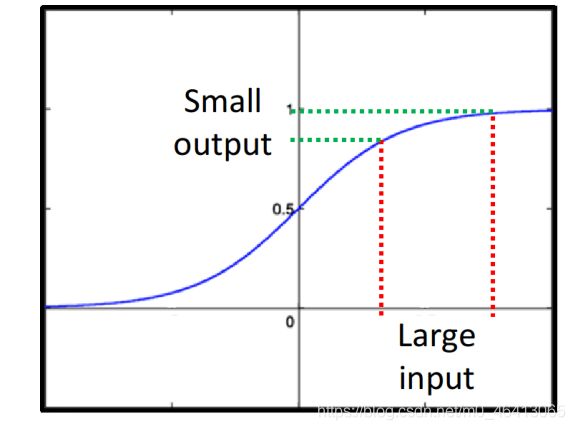
通过sigmoid function之后,得到output是会变⼩的,改变某⼀个参数的weight,会对某个neuron的output值产⽣影响,但是这个影响是会随着层数的递增⽽衰减的,sigmoid function的形状如下所⽰,它会把负⽆穷⼤到正⽆穷⼤之间的值都硬压到0~1之间,把较⼤的input压缩成较⼩的output
因此即使值很⼤,但每经过⼀个sigmoid function就会被缩⼩⼀次,所以network越深,被衰减的次数就越多,直到最后,它对output的影响就是⽐较⼩的,相应的也导致input对loss的影响会⽐较⼩,于是靠近input的那些weight对loss的gradient ∂ l ∂ w \frac{\partial l}{\partial w} ∂w∂l远⼩于靠近output的gradient
早年解决这个问题的做法是train RBM:先把第⼀个layer train好,再去train第⼆个,然后再第三个…
所以最后你在做Backpropagation的时候,尽管第⼀个layer⼏乎没有被train到,但⼀开始在做pre-train的时候就已经把它给train好了,这样RBM就可以在⼀定程度上解决问题。
但改activation function是目前handle这个问题的最好方法,之前在第三篇文章中提到了解决梯度消失的几种常见的activation function:
Activation Function Mindmap(干货!!!)
在这里就单个activation function再加以解释一下:
ReLU
Rectified Linear Unit(整流线性单元函数,⼜称修正线性单元),缩写为ReLU,该函数形状如下图所⽰,z为input,a为output,如果input>0则output = input,如果input<0则output = 0

李老师给了4点选择ReLU的理由:
- 跟sigmoid function⽐起来,ReLU的运算快很多
- ReLU的想法结合了⽣物上的观察( Pengel的paper )
- ⽆穷多bias不同的sigmoid function叠加的结果会变成ReLU
- ReLU可以处理Vanishing gradient的问题
Handle Vanishing gradient problem
我们重点介绍一下ReLU是怎样handle Vanishing gradient problem的
由ReLU表达式可知它neuron的output要么等于0, 要么等于input
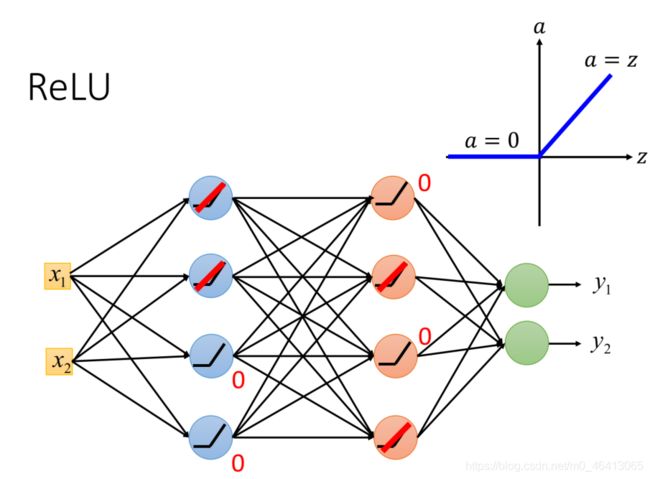
当output=input的时候,这个activation function就是linear的;⽽output=0的neuron对整个network是没有任何作⽤的,可以直接把它们去掉。
去掉所有output为0的neuron后

整个network就变成了⼀个瘦⻓的linear network, linear的好处是,output=input,不会像sigmoid function⼀样使input产⽣的影响逐层递减
李老师在这里问到了个问题,我们之所以使⽤deep learning,就是因为想要⼀个non-linear、⽐较复杂的function,⽽使⽤ReLU让它变成像上面那样的linear function,这样得到的function不是会变得很弱吗?
他是这样解释的,使⽤ReLU之后的network整体来说还是non-linear的,因为当input改变,导致neuron的operation region(input z<0/input z>0)被改变的话,整个network的结构被改变,⽐如从output=0转变到了output=input,也就是不同的输入可能会用到不同的neuron,从而从整个输入的dataset来看,其实每个神经元都可能被用到,实际上network整体来说还是non-linear的
还有个问题:ReLU是⼀个分段函数,它是不能微分的(⾄少在z=0这个点是不可微的),而对loss function做gradient descent,要求neural network是可以做微分的,这个怎么解决?
在实际操作上,当region的范围处于z>0时,微分值gradient就是1;当region的范围处于z<0时,微分值gradient就是0;当z为0时,就不要管它,相当于把它从network⾥⾯拿掉,就这么简单粗暴的处理方式
然后之后讲的就是ReLU的一些变式和Maxout,具体的看上面的mindmap就好了,我就不多做赘述了。
Adaptive learning rate
接着来讲在Training data上得到更好的performance的第二个方法:
Review - Adagrad
首先来回顾一下之前在第一篇文章中讲过的Adagrad的做法,老规矩,忘了回去补课:传送门
这个做法的宗旨就是让每⼀个parameter都要有不同的learning rate

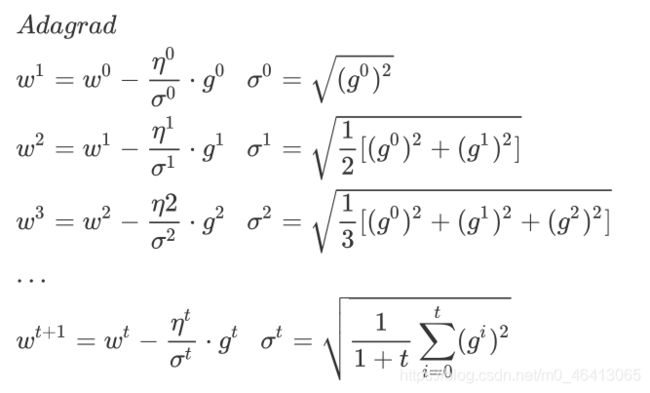
假设我们考虑两个参数w1,w2,
在w1这个⽅向上,平常的gradient都⽐较⼩, 那它是⽐较平坦的,于是就给它⽐较⼤learning rate;
在w2这个⽅向上,平常的gradient都⽐较⼤,那它是⽐较陡峭的,于是给它⽐较⼩的learning rate
但是,这样还面临着一个问题。
RMSProp
在下图所⽰的情况中,即使是在同⼀个⽅向上(如w1⽅向),loss function也有可能⼀会⼉平坦⼀会⼉陡峭,所以你要随时根据gradient的⼤⼩来快速地调整learning rate
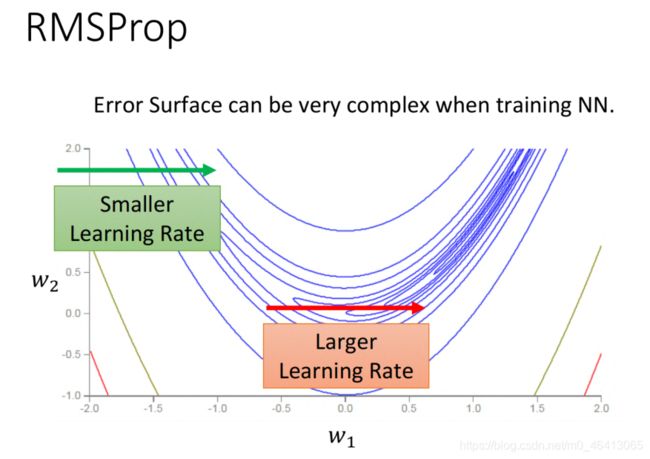
所以我们需要根据dynamic的调整learning rate的⽅法,于是搞出了Adagrad的进化版——RMSProp
How to do RMSProp
RMSProp的做法:
我们的learning rate依旧设置为⼀个固定的值η除掉⼀个变化的值σ,这个σ等于上⼀个σ和当前g梯度的加权⽅均根(特别的是,在第⼀个时间点,σ0就是第⼀个算出来的gradient值 g0 ),即:
这⾥的α值是可以⾃由调整的,RMSProp跟Adagrad不同之处在于:
Adagrad的分⺟是对过程中所有的gradient取平⽅和开根号,也就是说Adagrad考虑的是整个过程平均的gradient信息;
⽽RMSProp虽然也是对所有的gradient进⾏平⽅和开根号,但是它⽤⼀个α来调整对不同gradient的使⽤程度,⽐如你把α的值设的⼩⼀点,意思就是你更倾向于相信新的gradient所告诉你的error surface的平滑或陡峭程度,⽽⽐较⽆视于旧的gradient所提供给你的information
所以当你做RMSProp的时候,⼀样是在算gradient的root mean square,但是你可以给现在已经看到的gradient⽐较⼤的weight,给过去看到的gradient⽐较⼩的weight,来调整对gradient信息的使⽤程度
Momentum
除了learning rate的问题以外,在做deep learning的时候,也会出现卡在local minimum、saddle point或是plateau的地⽅,很多⼈都会担⼼,deep learning这么复杂的model,可能⾮常容易就会被卡住了
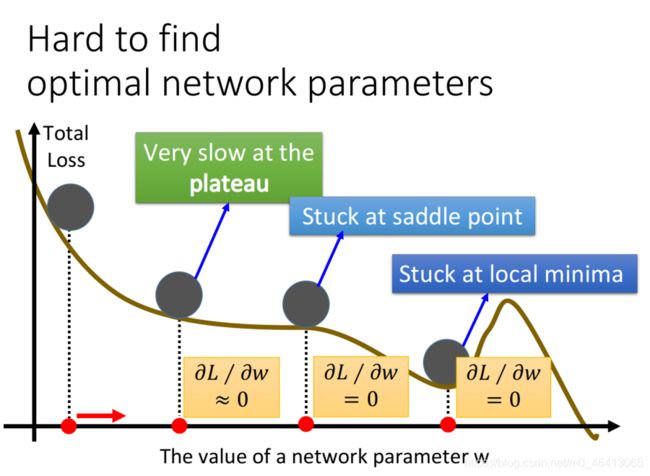
但其实Yann LeCun在07年的时候,就提出了⼀个蛮特别的说法,他说你不要太担⼼local minima的问题,因为⼀旦出现local minima,它就必须在每⼀个dimension都是下图中这种⼭⾕的低⾕形状,假设⼭⾕的低⾕出现的概率为p,由于我们的network有⾮常⾮常多的参数,这⾥假设有1000个参数,每⼀个参数都要位于⼭⾕的低⾕之处,这件事发⽣的概率为 p1000 ,当你的network越复杂,参数越多,这件事发⽣的概率就越低
所以在⼀个很⼤的neural network⾥⾯,其实并没有那么多的local minima,搞不好它看起来其实是很平滑的,所以当你⾛到⼀个你觉得是local minima的地⽅被卡住了,那它⼋成就是global minima,或 者是很接近global minima的地⽅。
where is Momentum from
虽然上面说不用在一卡住的问题,但我们还是给出了一种解决的办法(从物理里学来的惯性)
假设在有⼀个球从左上⻆滚下来,它会滚到plateau的地⽅、local minima的地⽅,但是由于惯性它还会继续往前⾛⼀段路程,假设前⾯的坡没有很陡,这个球就很有可能翻过⼭坡,⾛到⽐local minima还要好的地⽅

所以我们要做的,就是把惯性塞到gradient descent⾥⾯,这件事情就叫做Momentum
how to do Momentum
当我们在gradient descent⾥加上Momentum的时候,每⼀次update的⽅向,不再只考虑gradient的⽅向,还要考虑上⼀次update的⽅向,那这⾥我们就⽤⼀个变量v去记录前⼀个时间点update的⽅向随机选⼀个初始值θ0,初始化v0=0,接下来计算θ0处的gradient,然后我们要移动的⽅向是由前⼀个时间点的移动⽅向 v0 和gradient的反⽅向▽L(θ0)来决定的,即
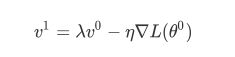
注:这⾥的λ也是⼀个⼿动调整的参数,它表⽰惯性对前进⽅向的影响有多⼤
接下来我们第⼆个时间点要⾛的⽅向 v2,它是由第⼀个时间点移动的⽅向v1和gradient▽L(θ1)的反⽅向共同决定的; λv是图中的绿⾊虚线,它代表由于上⼀次的惯性想要继续⾛的⽅向;η▽L(θ1)是图中的红⾊虚线,它代表这次gradient告诉你所要移动的⽅向;蓝⾊实线表示它们的⽮量和就是这⼀次真实移动的⽅向
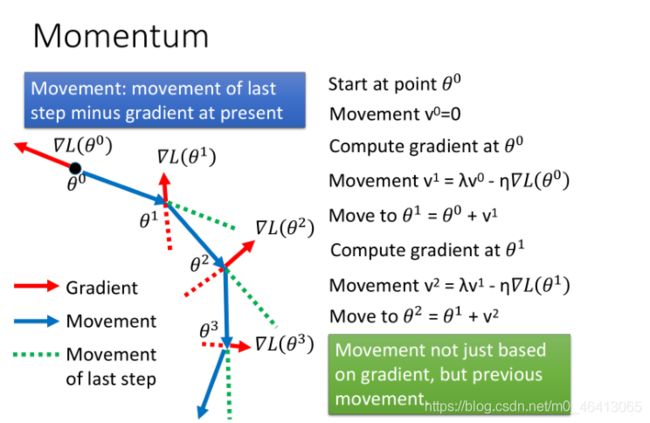
gradient告诉我们⾛红⾊虚线的⽅向,惯性告诉我们⾛绿⾊虚线的⽅向,合起来就是⾛蓝⾊的⽅向
我们还可以⽤另⼀种⽅法来理解Momentum这件事,其实你在每⼀个时间点移动的步伐 vi,包括⼤⼩和⽅向,就是过去所有gradient的加权和
具体推导如下图所⽰,第⼀个时间点移动的步伐v1是处的gradientθ0加权,第⼆个时间点移动的步伐v2是θ0和θ1处的gradient加权和…以此类推;由于λ的值⼩于1,因此该加权意味着越是之前的gradient, 它的权重就越⼩,也就是说,你更在意的是现在的gradient,但是过去的所有gradient也要对你现在update的⽅向有⼀定程度的影响⼒,这就是Momentum
我们形象的来看⼀下加⼊Momentum之后是怎么运作的:
(红⾊实线是gradient建议我们⾛的⽅向,直观上看就是根据坡度要⾛的⽅向;绿⾊虚线是
Momentum建议我们⾛的⽅向,实际上就是上⼀次移动的⽅向;蓝⾊实线则是最终真正⾛的⽅向)

在加⼊Momentum以后,每⼀次移动的⽅向,就是negative的gradient加上Momentum建议我们要⾛ 的⽅向,Momentum其实就是上⼀个时间点的movement
如果⾛到local minimum的地⽅,此时gradient是0,红⾊箭头没有指向,它就会告诉你就停在这⾥吧,但是Momentum也就是绿⾊箭头,它指向右侧就是告诉你之前是要⾛向右边的,所以你仍然应该要继续往右⾛,所以最后你参数update的⽅向仍然会继续向右;你甚⾄可以期待Momentum⽐较强,惯性的⼒量可以⽀撑着你⾛出这个⾕底,去到loss更低的地⽅
Adam
其实Adam就是RMSProp加上Momentum,
我们放出它的paper,不再多赘述了。

Good Results on Testing Data?
刚刚讲述了使Trainng data上得到更好的performance的两个方法。
现在我们来讲述如何在Testing data上得到更好的performance
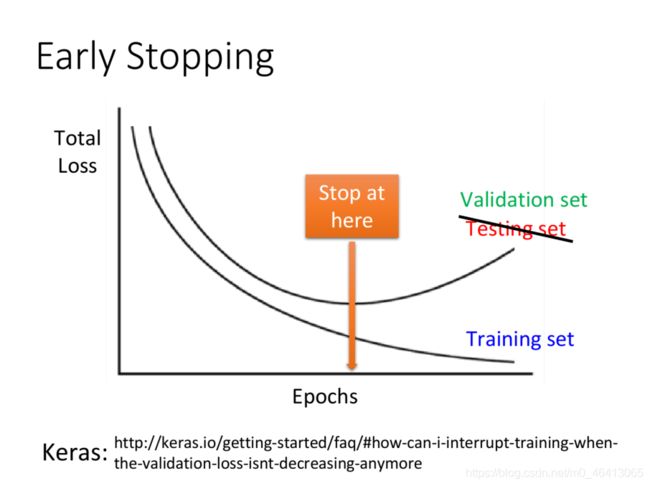
Early Stopping
假设你今天的learning rate调的⽐较好,那随着训练的进⾏,total loss通常会越来越⼩,但是Training set和Testing set的情况并不是完全⼀样的,很有可能当你在Training set上的loss逐渐减⼩的时候,在Testing set上的loss反⽽上升了
所以,理想上假如你知道testing data上的loss变化情况,你会在testing set的loss最⼩的时候停下来,⽽不是在training set的loss最⼩的时候停下来;但testing set实际上是未知的东西,所以我们需要⽤validation set来替代它去做这件事情。
注:很多时候,我们所讲的“testing set”并不是指代那个未知的数据集,⽽是⼀些已知的被你拿来做测试之⽤的数据集,⽐如kaggle上的public set,或者是你⾃⼰切出来的validation set
通俗的来讲就是我们自己手动的提前在效果最好的时候把程序停掉。
Regularization
这个之前在第一篇Regression中也提到了,这里就来复习下吧:
regularization就是在原来的loss function上额外增加⼏个term。
⽐如我们要minimize的loss function 原先应该是square error或cross entropy,那在做Regularization的时候,就在后⾯加⼀个Regularization的term。
L2 regularization
regularization term可以是参数的L2 norm(L2正规化),所谓的L2 norm,就是把model参数集 ⾥的每⼀个参数都取平⽅然后求和,这件事被称作L2 regularization,即
通常我们在做regularization的时候,新加的term⾥是不会考虑bias这⼀项的,因为加regularization的⽬的是为了让我们的function更平滑,⽽bias通常是跟function的平滑程度没有关系的
你会发现我们新加的regularization term λ ½ ∣ ∣ θ ∣ ∣ 2 λ½||θ||_2 λ½∣∣θ∣∣2 ⾥有⼀个½,由于我们是要对loss function求微分的,⽽新加的regularization term是参数 的平⽅和,对平⽅求微分会多出来⼀个系数2,我们的 就是⽤来和这个2相消的
L2 regularization具体⼯作流程如下:
如果把这个推导出来的式⼦和原式作⽐较,你会发现参数 在每次update之前,都会乘上⼀个
(1-ηλ) ,⽽ 和 通常会被设为⼀个很⼩的值,因此(1-ηλ) 通常是⼀个接近于1的值,⽐如0.99,;也就是说,regularization做的事情是,每次update参数 w i w_i wi之前,不分⻘红皂⽩就先对原来的 w i w_i wi乘个0.99,这意味着,随着update次数增加,参数 w i w_i wi会越来越接近于0
但问题是所有的参数都越来越靠近0,那最后岂不是 w i w_i wi通通变成0,得到的network还有什么⽤?
不过不会出现最后所有参数都变为0的情况,因为通过微分得到的 η ∂ L ∂ w i η\frac{\partial L}{\partial w_i} η∂wi∂L这⼀项是会和前⾯ ( 1 − η λ ) w i t (1-ηλ)w_i^t (1−ηλ)wit这⼀项最后取得平衡的
使⽤L2 regularization可以让weight每次都变得更⼩⼀点,这就叫做Weight Decay(权重衰减)
L1 regularization
除了L2 regularization中使⽤平⽅项作为new term之外,还可以使⽤L1 regularization,把平⽅项换成每⼀个参数的绝对值,即
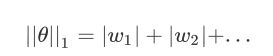
Tip:关于绝对值不能微分的处理,实际上只有在0的地⽅是不能微分的,那真的⾛到0的时候就胡乱给它⼀个值,⽐如0。
如果w是正的,那微分出来就是+1,如果w是负的,那微分出来就是-1,所以这边写了⼀个w的sign function,它的意思是说,如果w是正数的话,这个function output就是+1,w是负数的话,这个function output就是-1
L1 regularization的⼯作流程如下:
这个式⼦告诉我们,每次update的时候,都要减去⼀个 η λ s g n ( w i t ) ηλsgn(w_i^t) ηλsgn(wit),如果w是正的, sgn是+1,就会变成减⼀个positive的值让你的参数变⼩;如果w是负的,sgn是-1,就会变成加⼀个值 让你的参数变⼤;总之就是让它们的绝对值减⼩⾄接近于0
L1 V.s. L2
L1和L2,虽然它们同样是让参数的绝对值变⼩,但它们做的事情其实略有不同:
-
L1使参数绝对值变⼩的⽅式是每次update减掉⼀个固定的值
-
L2使参数绝对值变⼩的⽅式是每次update乘上⼀个⼩于1的固定值
因此,当参数w的绝对值⽐较⼤的时候,L2会让w下降得更快,⽽L1每次update只让w减去⼀个固定的 值,train完以后可能还会有很多⽐较⼤的参数;当参数w的绝对值⽐较⼩的时候,L2的下降速度就会变得很慢,train出来的参数平均都是⽐较⼩的,⽽L1每次下降⼀个固定的value,train出来的参数是⽐较sparse的,这些参数有很多是接近0的值,也会有很⼤的值
Dropout(重要)
这是DL中极为重要的一个方法:
How to do Dropout
Dropout是怎么做的呢?
Training
在training的时候,每次update参数之前,我们对每⼀个neuron(也包括input layer的“neuron”)做sampling(抽样) ,每个neuron都有p%的⼏率会被丢掉,如果某个neuron被丢掉的话,跟它相连的weight也都要被丢掉
实际上就是每次update参数之前都通过抽样只保留network中的⼀部分neuron来做训练
做完sampling以后,network structure就会变得⽐较细⻓了,然后你再去train这个细⻓的network
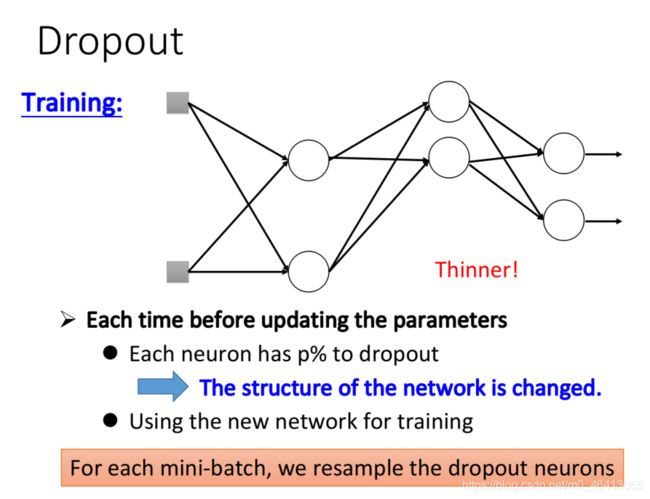
当你在training的时候使⽤dropout,得到的performance其实是会变差的,因为某些neuron在training的时候莫名其妙就会消失不⻅,但这并不是问题,因为:
== Dropout真正要做的事情,就是要让你在training set上的结果变差,但是在testing set上的结果是变好的==
Testing
在使⽤dropout⽅法做testing的时候要注意两件事情:
- testing的时候不做dropout,所有的neuron都要被⽤到
- 假设在training的时候,dropout rate是p%,从training data中被learn出来的所有weight都要乘上(1-p%)才能被当做testing的weight使⽤
![]()
Why Dropout?
为什么dropout会有⽤? 直接的想法是这样⼦:
在training的时候,会丢掉⼀些neuron,就好像是你要练轻功的时候,会在脚上绑⼀些重物;然后,你在实际战⽃的时候,就是实际testing的时候,是没有dropout的,就相当于把重物拿下来,所以你就会变得很强


为什么training和testing使⽤的weight是不⼀样的呢?
直觉的解释是这样的:
假设现在的dropout rate是50%,那在training的时候,你总是期望每次update之前会丢掉⼀半的neuron,就像下图左侧所⽰,在这种情况下你learn好了⼀组weight参数,然后拿去testing
但是在testing的时候是没有dropout的,所以如果testing使⽤的是和training同⼀组weight,那左侧得到的output z和右侧得到的output z‘,它们的值其实是会相差两倍的,即z’≈2z ,这样会造成testing 的结果与training的结果并不match,最终的performance反⽽会变差
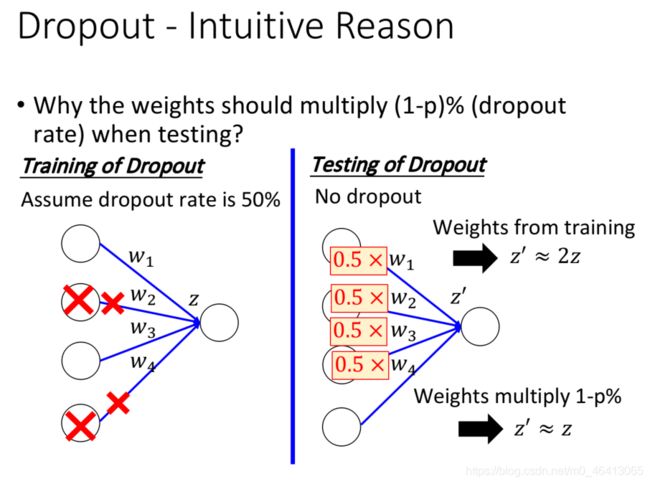
那这个时候,你就需要把右侧testing中所有的weight乘上0.5,然后做normalization,这样z就会等于z’,使得testing的结果与training的结果是⽐较match的
Dropout is a kind of ensemble
dropout 是⼀种终极的ensemble的⽅法!
ensemble精神的解释
ensemble的⽅法在⽐赛的时候经常⽤得到,它的意思是说,我们有⼀个很⼤的training set,那你每次都只从这个training set⾥⾯sample⼀部分的data出来,像下图⼀样,抽取了set1,set2,set3,set4
我们之前在讲bias和variance的trade off的时候说过,打靶有两种情况:
- ⼀种是因为bias⼤⽽导致打不准(参数过少)
- 另⼀种是因为variance⼤⽽导致打不准(参数过多)
假设我们今天有⼀个很复杂的model,它往往是bias⽐较准,但variance很⼤的情况,如果你有很多个笨重复杂的model,虽然它们的variance都很⼤,但最后平均起来,结果往往就会很准
所以ensemble做的事情,就是利⽤这个特性,我们从原来的training data⾥⾯sample出很多subset, 然后train很多个model,每⼀个model的structure甚⾄都可以不⼀样;在testing的时候,丢了⼀笔testing data进来,使它通过所有的model,得到⼀⼤堆的结果,然后把这些结果平均起来当做最后的output
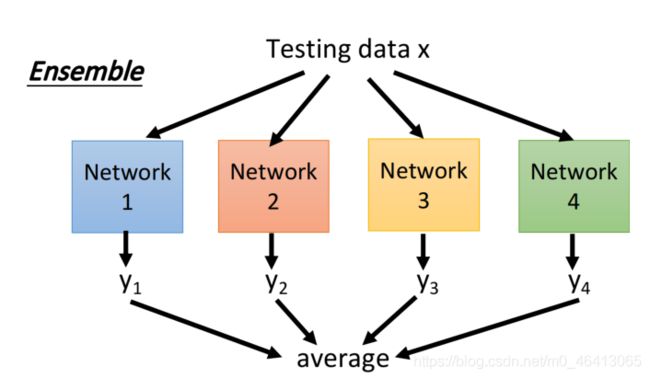
如果你的model很复杂,这⼀招往往是很有⽤的,那著名的random forest(随机森林)也是实践这个精神的⼀个⽅法,也就是如果你⽤⼀个decision tree,它就会很弱,也很容易overfitting,⽽如果采⽤random forest,它就没有那么容易overfitting
为什么dropout是⼀个终极的ensemble⽅法呢?
在training network的时候,每次拿⼀个minibatch出来就做⼀次update,⽽根据dropout的特性,每次update之前都要对所有的neuron进⾏sample,因此每⼀个minibatch所训练的network都是不同的
假设我们有M个neuron,每个neuron都有可能drop或不drop,所以总共可能的network数量有
个;所以当你在做dropout的时候,相当于是在⽤很多个minibatch分别去训练很多个network(⼀个minibatch⼀般设置为100笔data),由于update次数是有限的,所以做了⼏次update,就相当于train 了⼏个不同的network,最多可以训练到2M个network
每个network都只⽤⼀个minibatch的data来train,可能会让⼈感到不安,⼀个batch才100笔data,怎么train⼀个network呢?其实没有关系,因为这些不同的network之间的参数是shared,也就是说, 虽然⼀个network只能⽤⼀个minibatch来train,但同⼀个weight可以在不同的network⾥被不同的
minibatch train,所以同⼀个weight实际上是被所有没有丢掉它的network⼀起share的,它是拿所有这些network的minibatch合起来⼀起train的结果
实际操作ensemble的做法
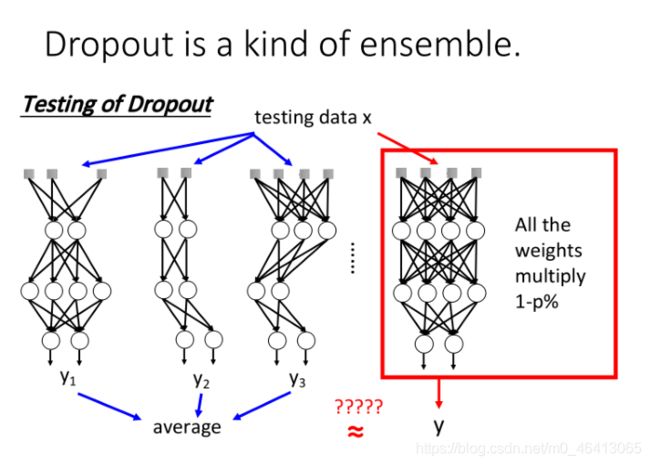
那按照ensemble这个⽅法的逻辑,在testing的时候,你把那train好的⼀⼤把network通通拿出来,然 后把⼿上这⼀笔testing data丢到这把network⾥⾯去,每个network都给你吐出⼀个结果来,然后你把所有的结果平均起来 ,就是最后的output
但是在实际操作上,如下图左侧所⽰,这⼀把network实在太多了,你没有办法每⼀个network都丢⼀ 个input进去,再把它们的output平均起来,这样运算量太⼤了
所以dropout最神奇的地⽅是,当你并没有把这些network分开考虑,⽽是⽤⼀个完整的network,这 个network的weight是⽤之前那⼀把network train出来的对应weight乘上(1-p%),然后再把⼿上这笔testing data丢进这个完整的network,得到的output跟network分开考虑的ensemble的output,是惊⼈的相近
也就是说下图左侧ensemble的做法和右侧dropout的做法,得到的结果是approximate(近似)的
举例说明dropout和ensemble的关系这⾥⽤⼀个例⼦来解释:
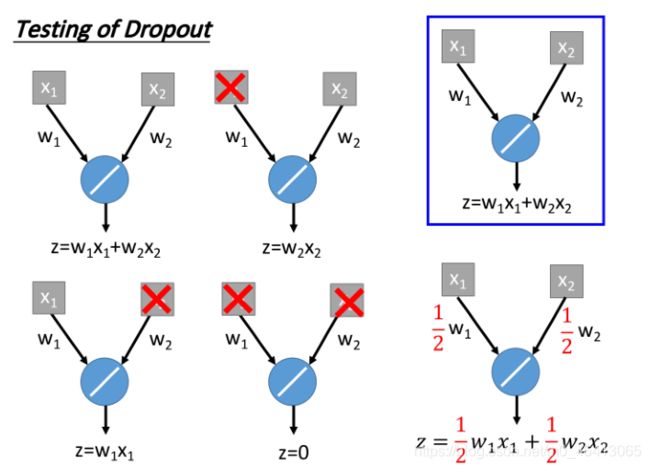
我们train⼀个下图右上⻆所⽰的简单的network,它只有⼀个neuron,activation function是linear
的,并且不考虑bias,这个network经过dropout训练以后得到的参数分别为 ,那给它input
,得到的output就是z=w1x1+w2x2
如果我们今天要做ensemble的话,theoretically就是像下图这么做,每⼀个neuron都有可能被drop或 不drop,这⾥只有两个input的neuron,所以我们⼀共可以得到2^2=4种network
我们⼿上这笔testing data 丢到这四个network中,分别得到4个output:
w1x1+w2x2,w2,w1x1,0,然后根据ensemble的精神,把这四个network的output通通都
average起来,得到的结果是½(w1x1+w2x2)
那根据dropout的想法,我们把从training中得到的参数 乘上(1-50%),作为testing network⾥的参数,也就是 w1’,w2’=(1-50%)(w1’,w2’)=0.5w1,0.5w2
这边想要呈现的是,在这个最简单的case⾥⾯,⽤不同的network structure做ensemble这件事情,跟我们⽤⼀整个network,并且把weight乘上⼀个值⽽不做ensemble所得到的output,其实是⼀样的
值得注意的是,只有是linear的network,才会得到上述的等价关系,如果network是⾮linear的, ensemble和dropout是不equivalent的;但是,dropout最后⼀个很神奇的地⽅是,虽然在non-linear 的情况下,它是跟ensemble不相等的,但最后的结果还是会work
如果network很接近linear的话,dropout所得到的performance会⽐较好,⽽ReLU和Maxout的
network相对来说是⽐较接近于linear的,所以我们通常会把含有ReLU或Maxout的network与
Dropout配合起来使⽤
到现在为止,Training data和Testing data的优化技巧我们都讲完了,但,有没有想过我们为什么要用那么深的神经网络?
Why Deep?
这节李宏毅老师讲的真是太棒了!超级形象!
不过老师也蜻蜓点水般的讲了一些NLP的例子,这里不是很懂的也没关系,我们理解老师的模块化思想就行,在这里抽取博主认为形象的例子来讲。
Shallow V.s. Deep
Deep is Better?
我们都知道deep learning在很多问题上的表现都是⽐较好的,越deep的network⼀般都会有更好的performance
那为什么会这样呢?有⼀种解释是:
⼀个network的层数越多,参数就越多,这个model就越复杂,它的bias就越⼩,⽽使⽤⼤量的data可以降低这个model的variance,performance当然就会更好
如下图所⽰,随着layer层数从1到7,得到的error rate不断地降低,所以有⼈就认为,deep learning的表现这么好,完全就是⽤⼤量的data去硬train⼀个⾮常复杂的model⽽得到的结果

既然⼤量的data加上参数⾜够多的model就可以实现这个效果,那为什么⼀定要⽤DNN呢?我们完全可以⽤⼀层的shallow neural network来做同样的事情,理论上只要这⼀层⾥neuron的数⽬⾜够多,有⾜够的参数,就可以表⽰出任何函数;那DNN中deep的意义何在呢?
Fat + Short v.s. Thin + Tall
其实深和宽这两种结构的performance是会不⼀样的,这⾥我们就拿下⾯这两种结构的network做⼀下
⽐较:
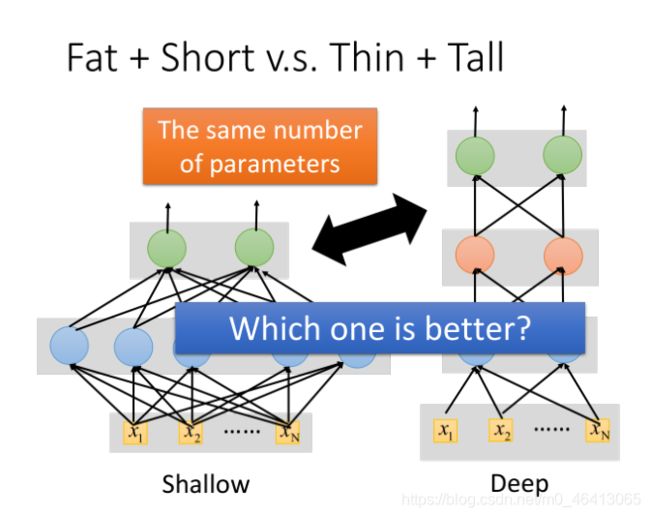
值得注意的是:如果要给Deep和Shallow的model⼀个公平的评⽐,你就要故意调整它们的形状,让它 们的参数是⼀样多的,在这个情况下Shallow的model就会是⼀个矮胖的model,Deep的model就会是
⼀个瘦⾼的model
在这个公平的评⽐之下,得到的结果如下图所⽰:
左侧表⽰的是deep network的情况,右侧表⽰的是shallow network的情况,为了保证两种情况下参数的数量是⽐较接近的,因此设置了右侧13772和14634这两种size⼤⼩,它们分别对应⽐较左侧52k 和72k这两种情况下的network(注意参数数⽬和neuron的数⽬并不是等价的)
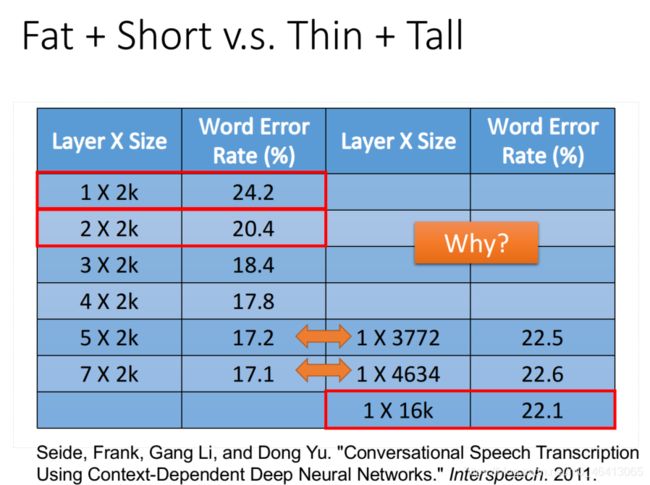
这个时候你会发现,在参数数量接近的情况下,只有1层的network,它的error rate是远⼤于好⼏层的network的;这⾥甚⾄测试了1×16k⼤⼩的shallow network,把它跟左侧也是只有⼀层,但是没有那么宽的network进⾏⽐较,由于参数⽐较多所以才略有优势;但是把116k⼤⼩的shallow network和参数远⽐它少的22k⼤⼩的deep network进⾏⽐较,结果竟然是后者的表现更好
也就是说,只有1层的shallow network的performance甚⾄都⽐不过很多参数⽐它少但层数⽐它多的deep network,这是为什么呢?
有⼈觉得deep learning就是⼀个暴⼒辗压的⽅法,我可以弄⼀个很⼤很⼤的model,然后collect⼀⼤堆的data,就可以得到⽐较好的performance;但根据上⾯的对⽐可知,deep learning显然是在结构上存在着某种优势,不然⽆法解释它会⽐参数数量相同的shallow learning表现得更好这个现象
Modularization
introduction
DNN结构⼀个很⼤的优势是,Modularization(模块化),它⽤的是结构化的架构
example
这⾥举⼀个分类的例⼦,我们要把input的⼈物分为四类:⻓头发⼥⽣、⻓头发男⽣、短头发⼥⽣、短头发男⽣
如果按照shallow network的想法,我们分别独⽴地train四个classifier(其实就相当于训练四个独⽴的model),然后就可以解决这个分类的问题;但是这⾥有⼀个问题,⻓头发男⽣的data是⽐较少的,没有太多的training data,所以,你train出来的classifier就⽐较weak,去detect⻓头发男⽣的performance就⽐较差

但其实我们的input并不是没有关联的,⻓头发的男⽣和⻓头发的⼥⽣都有⼀个共同的特征,就是⻓头 发,因此如果我们分别独⽴地训练四个model作为分类器,实际上就是忽视了这个共同特征,也就是没 有⾼效地⽤到data提供的全部信息,这恰恰是shallow network的弊端
⽽利⽤modularization的思想,使⽤deep network的架构,我们可以训练⼀个model作为分类器就可以完成所有的任务,我们可以把整个任务分为两个⼦任务:
- Classifier1:检测是男⽣或⼥⽣
- Classifier2:检测是⻓头发或短头发
虽然⻓头发的男⽣data很少,但⻓头发的⼈的data就很多,经过前⾯⼏层layer的特征抽取,就可以头发的data全部都丢给Classifier2,把男⽣或⼥⽣的data全部都丢给Classifier1,这样就真正做到了充 分、⾼效地利⽤数据,最终的Classifier再根据Classifier1和Classifier2提供的信息给出四类⼈的分类结果

你会发现,经过层层layer的任务分解,其实每⼀个Classifier要做的事情都是⽐较简单的,⼜因为这种分层的、模组化的⽅式充分利⽤了data,并提⾼了信息利⽤的效率,所以只要⽤⽐较少的training data 就可以把结果train好
deep -> modularization
做modularization的好处是把原来⽐较复杂的问题变得简单,⽐如原来的任务是检测⼀个⻓头发的⼥
⽣,但现在你的任务是检测⻓头发和检测性别,⽽当检测对象变简单的时候,就算training data没有那么多,我们也可以把这个task做好,并且所有的classifier都⽤同⼀组参数检测⼦特征,提⾼了参数使
⽤效率,这就是modularization、这就是模块化的精神
由于deep learning的deep就是在做modularization这件事,所以它需要的training data反⽽是⽐较少的,这可能会跟你的认知相反,AI=big data+deep learning,但deep learning其实是为了解决less data的问题才提出的
每⼀个neuron其实就是⼀个basic的classifier:
- 第⼀层neuron,它是⼀个最basic的classifier,检测的是颜⾊、线条这样的⼩特征
- 第⼆层neuron是⽐较复杂的classifier,它⽤第⼀层basic的classifier的output当作input,也就是把第⼀层的classifier当作module,利⽤第⼀层得到的⼩特征分类出不同样式的花纹
- ⽽第三层的neuron⼜把第⼆层的neuron当作它module,利⽤第⼆层得到的特征分类出蜂窝、轮胎、⼈
- 以此类推

这边要强调的是,在做deep learning的时候,怎么做模块化这件事情是machine⾃动学到的,也就是说,第⼀层要检测什么特征、第⼆层要检测什么特征…这些都不是⼈为指定的,⼈只有定好有⼏层layer、每层layer有⼏个neuron,剩下的事情都是machine⾃⼰学到的
传统的机器学习算法,是⼈为地根据domain knowledge指定特征来进⾏提取,这种指定的提取⽅式, 甚⾄是提取到的特征,也许并不是实际最优的,所以它的识别成功率并没有那么⾼;但是如果提取什么 特征、怎么提取这件事让机器⾃⼰去学,它所提取的就会是那个最优解,因此识别成功率普遍会⽐⼈为 指定要来的⾼
剪窗花(超级形象)
我们之前讲过这个逻辑回归的分类问题,可能会出现下⾯这种linear model根本就没有办法分类的问题,⽽当你加了hidden layer的时候,就相当于做了⼀个feature transformation,把原来的x1,x2转换到另外⼀个平⾯,变成x1’、x2’
你会发现,通过这个hidden layer的转换,其实就好像把原来这个平⾯按照对⻆线对折了⼀样,对折后两个蓝⾊的点就重合在了⼀起,这个过程跟剪窗花很像:
- 我们在做剪窗花的时候,每次把⾊纸对折,就相当于把原先的这个多维空间对折了⼀次来提⾼维度
- 如果你在某个地⽅戳⼀个洞,再把⾊纸打开,你折了⼏折,在对应的这些地⽅就都会有⼀个洞;这 就相当于在折叠后的⾼维空间上,画斜线的部分是某⼀个class,不画斜线的部分是另⼀个class, 那你在这个⾼维空间上的某⼀个点,就相当于展开后空间上的许多点,由于可以对这个空间做各种 各样复杂的对折和剪裁,所以⼆维平⾯上⽆论多少复杂的分类情况,经过多次折叠,不同class最 后都可以在⼀个⾼维空间上以⽐较明显的⽅式被分隔开来
这样做既可以解决某些情况下难以分类的问题,⼜能够以⽐较有效率的⽅式充分利⽤data(⽐如下⾯这 个折纸,⾼维空间上的1个点等于⼆维空间上的5个点,相当于1笔data发挥出5笔data的作⽤)
下⾯举了⼀个⼩例⼦:
左边的图是training data,右边则是1层hidden layer与3层hidden layer的不同network的情况对⽐, 这⾥已经控制它们的参数数量趋于相同,试验结果是,当training data为10w笔的时候,两个network 学到的样⼦是⽐较接近原图的,⽽如果只给2w笔training data,1层hidden layer的情况就完全崩掉了,⽽3层hidden layer的情况会⽐较好⼀些,它其实可以被看作是剪窗花的时候⼀不⼩⼼剪坏了,然后展开得到的结果
注:关于如何得到model学到的图形,可以⽤固定model的参数,然后对input进⾏梯度下降,最终得到结果,具体⽅法⻅前⼏章
参考文章
为什么神经网络会出现梯度消失和梯度爆炸?
https://github.com/Sakura-gh/ML-notes