机器学习数学基础
目录
- 1 线性代数
-
- 1.1 矩阵定义
- 1.2 矩阵中的概念
-
- 1.2.1 向量
- 1.3 矩阵的运算
- 1.4 矩阵的转置
- 1.5 矩阵的逆
- 2 微积分
-
- 2.1 导数的定义
- 2.2 偏导数
- 2.3 方向导数
- 2.4 梯度
- 2.5 凸函数和凹函数
- 3 概率统计
-
- 3.1 常用统计变量
-
- 3.1.1 数学期望和大数定律
- 3.1.2 协方差
- 3.1.3 相关系数
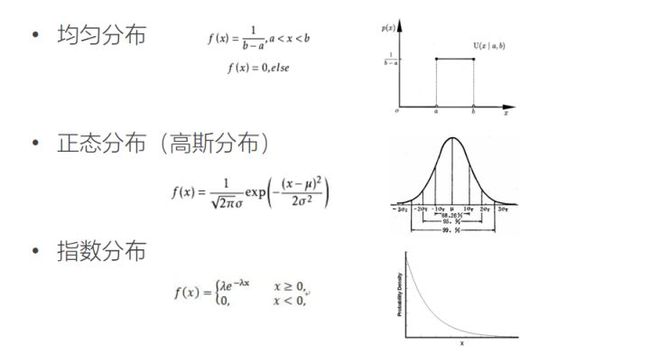
- 3.2 常见概率分布
- 3.3 重要概率公式
1 线性代数
导语:这些只是很基础的大学数学课本中的知识,如果考研的话,似乎看完这些也只是个知识点回顾,对做题并没有什么帮助.但是对于机器学习这些知识是必知必会的,要不然容易遇到看不懂!
1.1 矩阵定义
由 m × n 个数 aij (i = 1,2,…,m; j = 1,2,…,n) 排成的 m 行 n 列的数表 A 就称为 m 行 n 列的矩阵
这 m × n 个数称作矩阵 A 的元素,元素 aij 位于矩阵 A 的第 i 行第 j 列
m × n 矩阵 A 可以记作 Am×n,其中 m是行数,n是列数,m, n > 0
对于Am×n,如果 m = n,即矩阵的行数与列数相等,那么称A为方阵
1.2 矩阵中的概念
1.2.1 向量

有些时候看到向量是横着写,有时候是竖着写,其实列向量横着写然后加转置符号,其实就是和竖着写一摸一样,之所以要横着写是为了有些出版社和作者为了节省纸张与空间,横着写加转置多么节省空间,这个其中并没有什么规定非要横着写或者竖着写.
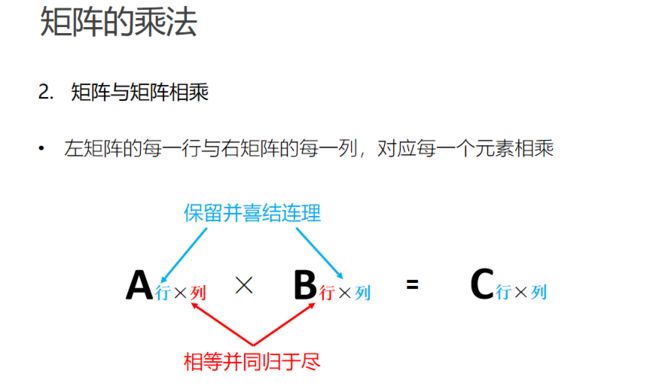
1.3 矩阵的运算
如果是同型矩阵或者是同行同列的就可以进行加减,就是对应的每个元素加减

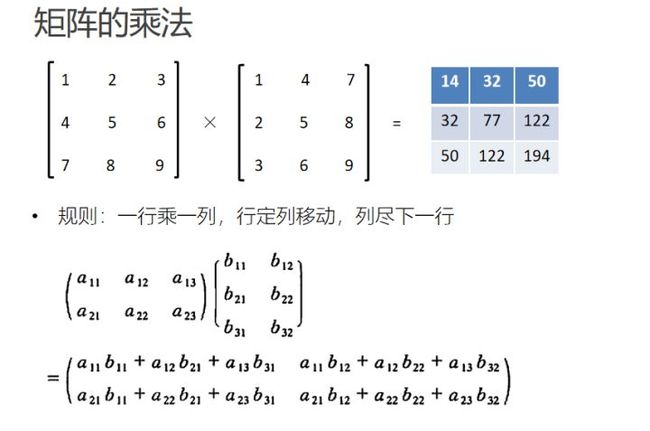
注意:A × B,那么有 A 矩阵 m × n,B 矩阵 n × k,要求左侧矩阵的列数 n,必须等于右侧矩阵的行数 n,结果矩阵 C 为 m × k 矩阵。
1.4 矩阵的转置
1.5 矩阵的逆

补充一下:矩阵的秩A=(aij)m×n的不为零的子式的最大阶数称为矩阵A的秩,记作rA,或rankA或R(A)。特别规定零矩阵的秩为零。r(A)<=min(m,n),A是m*n型矩阵,也就是最小的内个数是矩阵的秩.
2 微积分
2.1 导数的定义
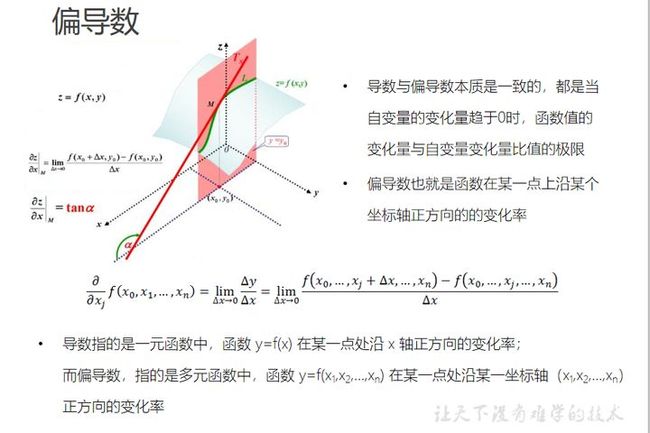
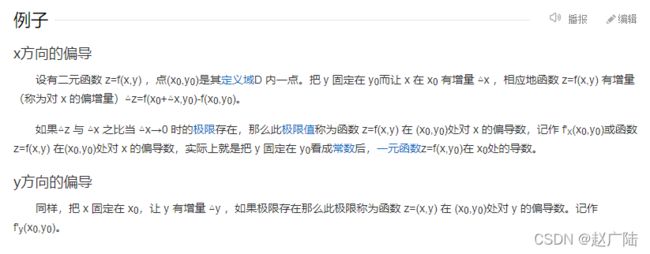
2.2 偏导数
2.3 方向导数
2.4 梯度
2.5 凸函数和凹函数
3 概率统计
3.1 常用统计变量
方差和标准差就是一种离散程度,离散程度越大说明数据的差值距离均值越大,方差越小说明数值越稳定.

均方误差(MSE)和均方根误差(RMSE)和平均绝对误差(MAE)
均方根误差,亦称标准误差
RMSE
Root Mean Square Error,均方根误差
是观测值与真值偏差的平方和与观测次数m比值的平方根。
是用来衡量观测值同真值之间的偏差
MAE
Mean Absolute Error ,平均绝对误差
是绝对误差的平均值
能更好地反映预测值误差的实际情况.
标准差
Standard Deviation ,标准差
是方差的算数平方根
是用来衡量一组数自身的离散程度
简单来说,标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
3.1.1 数学期望和大数定律
大数定律说如果统计数据足够大,那么事物出现的频率就能无限接近它的期望值。
也就是如果某城市增长到100万人口那么每个家庭中的孩子也就逼近于某个数.
可能不好理解
拿我们最熟悉的投色子举例,游戏规则是投中1点获得1元,投中2点获得2元,以此类推。
![]()
这个期望3.5代表什么意思呢?不是最后能拿到3.5元
而是,只要你一直玩下去,你每次游戏的预期收益是3.5元。可能你某次赢了1元,某一次赢了6元,只要你长期投下去, 你平均下来每次就赢3.5元。
3.1.2 协方差
协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
概念比较难以理解简单的说:
3.1.3 相关系数
弥补XY的相似程度的计算,就可以更清晰的得到相关性.