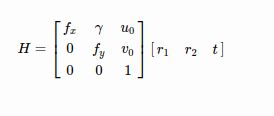3D视觉(二)：单目摄像头的标定与校正

3D视觉(二)：单目摄像头的标定与校正

相机将三维世界中的坐标点（单位为米）映射到二维图像平面（单位为像素），这个过程可用针孔相机模型和透镜畸变模型来刻画。这两个模型能够把外部的三维点投影到相机内部成像平面，构成相机的内参数。

---

一、相机模型

假设存在一个机器小车，以小车后轮为3D坐标原点可建立机器车坐标系。机器小车上携带有一个单目摄像头，以摄像头光心为3D坐标原点可建立相机坐标系。现已知某个物体在机器车坐标系下的3D坐标，如何计算出它在成像图像上像素点的2D索引位置？

1、机器车坐标系到相机坐标系

第1步：利用外参矩阵进行3D坐标变换。记旋转矩阵为R、平移向量为t，设物体在机器小车坐标系下的3D坐标为Pw，在相机坐标系下的3D坐标为P = (X, Y, Z)，则：

P = RPw + t = TPw

这里Pw和P的坐标单位都是米。

2、相机坐标系到归一化平面坐标系

第2步：利用针孔相机模型将3D相机坐标P = (X, Y, Z) 转化成2D归一化平面坐标 (x, y, 1)。

利用相似三角形原理，可以得到：z/f = x/X = y/Y。
一般我们取z = 1，得到映射后的归一化坐标为(x, y, z) = (X/f, Y/f, 1)，这里x、y的单位都是米。

归一化坐标可以看成相机前方z=1处平面上的一个点，这个z=1的平面也称为归一化平面。归一化平面再左乘内参矩阵，就可以得到像素坐标，所以我们可以把像素坐标(u, v)看成对归一化平面上的点进行量化测量的结果。

从这个模型也可以看出，如果对相机坐标同时乘以任何非零常数，归一化坐标都是一样的，这说明点的深度在投影过程中被丢失了，所以单目视觉中没法得到像素点的深度值。

3、归一化平面坐标畸变

第3步：对归一化坐标做畸变处理。为获得更好的成像效果，有时我们会在相机的前方加入透镜。透镜的加入会对成像过程中光线的传播产生新的影响。一是透镜自身的形状对光线传播存在影响；二是机械组装过程中透镜和成像平面不可能完全平行，这也会使得光线穿过透镜投影到成像平面时的位置发生变化。

由透镜形状引起的畸变称为径向畸变。在针孔模型中，一条直线投影到像素平面上还是一条直线，但在实际拍摄过程中，往往会出现真实环境中的一条直线在图片中变成了曲线，越靠近图像的边缘，这种现象越明显。畸变主要分为两类：桶形畸变、枕形畸变。桶形畸变图像放大率随着与光轴之间的距离增加而减小，而枕形畸变图像放大率随着与光轴之间的距离增加而增大。

由相机组装过程中不能使透镜和成像平面严格平行，由此引起的畸变成为切向畸变。

记归一化平面坐标为(x, y)，极坐标形式为(r, theta)，畸变坐标为(x_distorted, y_distorted)，它们之间的转换关系可用多项式进行描述：

径向畸变：

切向畸变：

综合以上两种畸变，得到畸变坐标：

这里x_distorted, y_distorted的单位是米。

4、归一化平面坐标系到像素坐标系

第4步：将畸变后的坐标(x_distorted, y_distorted)投影到像素平面，得到该点在图像上的位置。

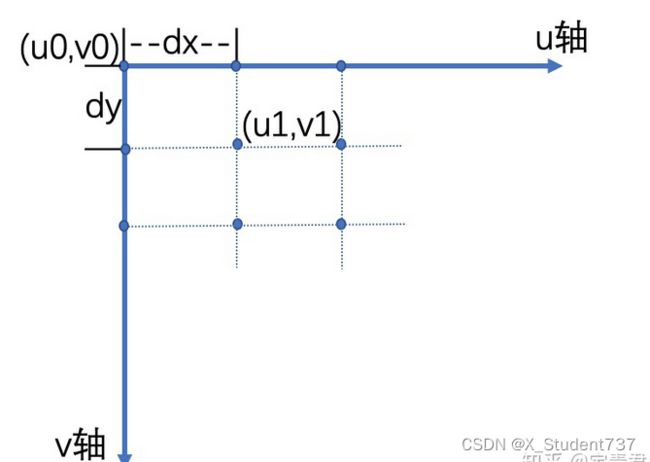
像素坐标与归一化平面坐标之间，相差了一个缩放和一个原点的平移。我们设像素坐标在u轴上缩放了fx倍，在v轴缩放了fy倍，同时原点平移了(cx. cy)，则畸变后的坐标(x_distorted, y_distorted) 和像素坐标(u, v)的关系为：

u = fx * x_distorted + cx
v = fy * y_distorted + cy

有时我们不考虑畸变模型，可直接对归一化坐标x、y进行平移缩放，得到像素坐标u、v。这里x_distorted, y_distorted、x、y的单位都是米，u、v的单位是像素，fx、fy的单位是像素/米，cx、cy的单位是像素。

二、单目摄像头标定

通常认为，相机的内参矩阵在出厂后是固定的，不会在使用过程中发生变换。有些相机生产厂商会告诉你相机的内参，而有时需要我们自己手动确定相机的内参，也就是所谓的标定。此外，如果觉得标定过程过于麻烦且对精度要求不高，可采用如下方法近似内参矩阵和畸变系数向量：

记图像尺寸为 (h, w) = (size[0], size[1])，对于内参矩阵K= [[fx, 0, cx], [0, fy, cy], [0, 0, 1]，可近似 fx = fy = size[1]，cx = size[1]/2，cy = size[0]/2。对于畸变系数向量D，可近似 D=zeros(1, 5)。

“张氏标定”是张正友教授于1998年提出的单平面棋盘格的摄像机标定方法，张氏标定法已经作为工具箱或封装好的函数被广泛应用，原文为“A Flexible New Technique for Camera Calibration”。此文中所提到的方法，为相机标定提供了很大便利，并且具有很高的精度。从此标定可以不需要特殊的标定物，只需要一张打印出来的棋盘格。

张氏标定就是利用一张打印的棋盘格，然后对每个角点进行标记其在像素坐标系的像素点坐标，以及在世界坐标系的坐标，通过4组以上的点就可以求解出H矩阵的值。但为减少误差，具有更强的鲁棒性，我们一般会拍摄许多张照片，选取大量的角点进行标定。

我们假设标定棋盘位于世界坐标中zw=0平面，则可得到简化公式：

定义H矩阵为：
则原方程可化为：

借助OpenCV棋盘格内点检测函数，我们可得到u、v的观测值。由于棋盘格是按照一定顺序规律排列的，所以可以将对应的索引赋值成它们的3D坐标点，虽然和真实世界坐标具有尺寸差异，但这只会影响外参矩阵的计算结果，而不影响内参矩阵的求解。这样我们得到了(u, v, 1 )和(xw. yw, 1)的对应观测值，通过线性方程组求解即可解出H矩阵。再通过旋转矩阵、内参矩阵的特殊性质，可从H矩阵中还原出内参矩阵K、旋转矩阵R和平移向量t。

具体标定过程如下：
step1: 准备一张棋盘格图片，固定在墙上。
step2: 从不同角度拍摄棋盘格一系列照片，存储在文件夹内。
step3: 对于每张拍摄的棋盘图片，检测图片中所有棋盘格的特征点(u, v, 1 )。
step4: 对于每张拍摄的棋盘图片，将对应的索引赋值成它们的3D坐标点(xw. yw, 1)。
step5: 利用cv::calibrateCamera函数进行标定，求解参数优化问题。
step6: 利用cv::undistort函数，对原图像进行校正。

三、实验结果

从不同角度拍摄棋盘格一系列照片，如图所示：
对每张图片进行棋盘格内点检测：

标定得到的参数结果为：

原图和校正后的图像如下图所示，可以看到畸变被很大程度上消除。

四、源码

单目相机标定：

#include 
// opencv.hpp中己经包含了OpenCV各模块的头文件，如高层GUI图形用户界面模块头文件highgui.hpp、图像处理模块头文件imgproc.hpp、2D特征模块头文件features2d.hpp等。
// 所以我们在编写应用程序时，原则上仅写上一句 #include  即可，这样可以精简优化代码
#include 
// calib3d模块主要是相机校准和三维重建相关的内容：基本的多视角几何算法，单个立体摄像头标定，物体姿态估计，立体相似性算法，3D信息的重建等。
#include 
// highgui模块，高层GUI图形用户界面，包含媒体的I/O输入输出、视频捕捉、图像和视频的编码解码、图形交互界面的接口等内容
#include 
// imgproc模块，图像处理模块，包含：线性和非线性的图像滤波、图像的几何变换、特征检测等

#include 
#include 
// unistd.h是用于linux/unix系统的调用，相当于windows下的windows.h，包含了许多UNIX系统服务的函数原型，例如read函数、write函数、sleep函数。
#include 
// chrono是C++11新加入的方便时间日期操作的标准库，它既是相应的头文件名称，也是std命名空间下的一个子命名空间，所有时间日期相关定义均在std::chrono命名空间下。
// 通过这个新的标准库，可以非常方便进行时间日期相关操作。 


using namespace std;


// 定义棋盘格维度，{6,4}代表行内点数为6，列内点数为4
int CHECKERBOARD[2]{6,4}; 

int main()
{
  
  // objpoints中每个元素都是一个小vector，每个小vector存储的每个元素都是opencv的cv::Point3f数据结构
  // n * 54 * 3 * 1
  std::vector<std::vector<cv::Point3f> > objpoints;

  // imgpoints中每个元素都是一个小vector，每个小vector存储的每个元素都是opencv的cv::Point2f数据结构
  // n * 54 * 2 * 1
  std::vector<std::vector<cv::Point2f> > imgpoints;

  // objp: 54 * 3 * 1, 记录单张棋盘格，54个内点的3d位置索引
  // 指定棋盘格坐标点时，按照先从上到下，后从左到右的顺序记录。每一行棋盘格的记录方式：(y索引, x索引， 0）
  std::vector<cv::Point3f> objp;
  //  [0, 0, 0;
  //  1, 0, 0;
  //  2, 0, 0;
  //  3, 0, 0;
  //  ... ...
  //  2, 8, 0;
  //  3, 8, 0;
  //  4, 8, 0;
  //  5, 8, 0]
  
  for(int i{0}; i<CHECKERBOARD[1]; i++)
  {
    for(int j{0}; j<CHECKERBOARD[0]; j++)
      objp.push_back(cv::Point3f(j,i,0));
  }


  // images_path，存储所有棋盘格图片的存储路径
  std::vector<cv::String> images_path;
  std::string path = "../images2/*.jpg";
  cv::glob(path, images_path);
  std::string saved_path;

  cv::Mat frame, gray;
  
  // corner_pts，记录检测到的棋盘格54个内点的2D像素坐标 
  std::vector<cv::Point2f> corner_pts;
  // success，用于判断是否成功检测到棋盘格
  bool success;

  // 开始计时
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  
  for(int i{0}; i<images_path.size(); i++)
  { 
    chrono::steady_clock::time_point t11 = chrono::steady_clock::now();
    
    // 图像大小 640 x 480
    frame = cv::imread(images_path[i]);
    std::cout << images_path[i] << std::endl;
    cv::cvtColor(frame,gray, cv::COLOR_BGR2GRAY);

    // OpenCV函数寻找棋盘格
    success = cv::findChessboardCorners(gray,cv::Size(CHECKERBOARD[0],CHECKERBOARD[1]), corner_pts, cv::CALIB_CB_ADAPTIVE_THRESH | cv::CALIB_CB_FAST_CHECK | cv::CALIB_CB_NORMALIZE_IMAGE);

    if(success)
    {
      cv::TermCriteria criteria(cv::TermCriteria::EPS | cv::TermCriteria::MAX_ITER, 30, 0.001);

      // 进一步refine检测到的网格内点的坐标精度
      // 这里cornerSubPix函数直接在原有corner_pts基础上进行覆盖，不会多创建一个新的变量再赋值
      cv::cornerSubPix(gray, corner_pts, cv::Size(11,11), cv::Size(-1,-1), criteria);

      // 作图，棋盘格检测结果
      cv::drawChessboardCorners(frame, cv::Size(CHECKERBOARD[0],CHECKERBOARD[1]), corner_pts, success);

      objpoints.push_back(objp);
      imgpoints.push_back(corner_pts);
    }
    
//     cv::imshow("Image", frame);
//     cv::waitKey(10);
    
    saved_path = "../images1_demo/" + std::to_string(i) + ".jpg";
    cv::imwrite(saved_path, frame);
    
    chrono::steady_clock::time_point t22 = chrono::steady_clock::now();
    chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t22 - t11);
    cout << "每一张图片处理耗时: " << time_used.count() << " 秒. " << endl;

  }

  cv::destroyAllWindows();
  
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used1 = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "整体耗时: " << time_used1.count() << " 秒. " << endl;

  
  // 内参矩阵、畸变系数、旋转矩阵R、平移向量T
  cv::Mat cameraMatrix, distCoeffs, R, T;

  chrono::steady_clock::time_point t111 = chrono::steady_clock::now();
  
  // 这里注意参数顺序，必须先cols后rows
  cv::calibrateCamera(objpoints, imgpoints, cv::Size(gray.cols,gray.rows), cameraMatrix, distCoeffs, R, T);
  
  chrono::steady_clock::time_point t222 = chrono::steady_clock::now();
  chrono::duration<double> time_used_cali = chrono::duration_cast<chrono::duration<double>>(t222 - t111);
  cout << "矫正耗时: " << time_used_cali.count() << " 秒. " << endl;

  
  std::cout << "cameraMatrix : " << cameraMatrix << std::endl;
  std::cout << "distCoeffs : " << distCoeffs << std::endl;
//   std::cout << "Rotation vector : " << R << std::endl;
//   std::cout << "Translation vector : " << T << std::endl;

  return 0;
}



// 对于相机内参矩阵：[[fx, 0, cx], [0, fy, cy], [0, 0, 1]
//  一般都可近似 fx = fy = size[1], cx = size[1]/2, cy = size[0]/2

// images2文件夹，内参标定结果：
// cameraMatrix : [845.5595871866724, 0, 1324.600361657917;
// 0, 850.5931334946969, 729.9380327446599;
// 0, 0, 1]
// distCoeffs : [-0.1129616696736557, 0.01545728211105597, -0.001661835061769386, -0.0001092622724212072, -0.001159949110844942]

单目相机校正：

#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;


int main()
{
  // images_path，存储所有棋盘格图片的存储路径
  std::vector<cv::String> images_path;
  std::string path = "../images2/*.jpg";
  cv::glob(path, images_path);
  
  // 根据计算得到的内参、畸变系数，对畸变图片进行矫正
  cv::Mat image;
  image = cv::imread(images_path[0]);
  cv::Mat dst, map1, map2, new_camera_matrix;
  cv::Size imageSize(cv::Size(image.cols, image.rows));
  
  // 内参矩阵
  float K[3][3] = {845.5595871866724, 0, 1324.600361657917, 0, 850.5931334946969, 729.9380327446599, 0, 0, 1};    // float类型
  cv::Mat cameraMatrix = cv::Mat(3, 3, CV_32FC1, K);    

  // 畸变系数 
  float d[1][5] = {-0.1129616696736557, 0.01545728211105597, -0.001661835061769386, -0.0001092622724212072, -0.001159949110844942};   // float类型 
  cv::Mat distCoeffs = cv::Mat(1, 5, CV_32FC1, d);   
   
  // 将内参矩阵和畸变系数进行融合，得到新的矫正参数矩阵
  // 最后一个参数需要注意：最后一个参数默认是false，也就是相机光心不在默认的图像中心位置，可能导致去除畸变后的图像边缘仍存在畸变，因此需要改成true
  new_camera_matrix = cv::getOptimalNewCameraMatrix(cameraMatrix, distCoeffs, imageSize, 0.01, imageSize, 0, true);
    
  for(int i{0}; i<images_path.size(); i++)
  {  
        
    image = cv::imread(images_path[i]); 

    // 第1种方法：OpenCV undistort函数，转换图像以补偿径向和切向镜头失真
    cv::undistort(image, dst, new_camera_matrix, distCoeffs, new_camera_matrix);

    // 第2种方法：OpenCV remap函数，计算联合不失真和整流变换，并以重映射的映射形式表示结果
    //   cv::initUndistortRectifyMap(cameraMatrix, distCoeffs, cv::Mat(),cv::getOptimalNewCameraMatrix(cameraMatrix, distCoeffs,   imageSize, 1, imageSize, 0),imageSize, CV_16SC2, map1, map2);
    // 
    //   cv::remap(image, dst, map1, map2, cv::INTER_LINEAR);
     
    cv::Mat resize_dst;
    resize(dst, resize_dst, cv::Size(256*2, 144*2), 0, 0, cv::INTER_LINEAR);

    cv::imshow("undistorted image", resize_dst);
    cv::waitKey(0);  
    
    std::string saved_path = "../images2_undist/" + std::to_string(i) + ".jpg";
    cv::imwrite(saved_path, dst);
    
  }

  return 0;
}

五、相关链接

如果代码跑不通，或者想直接使用我自己制作的数据集，可以去下载项目链接：
https://blog.csdn.net/Twilight737