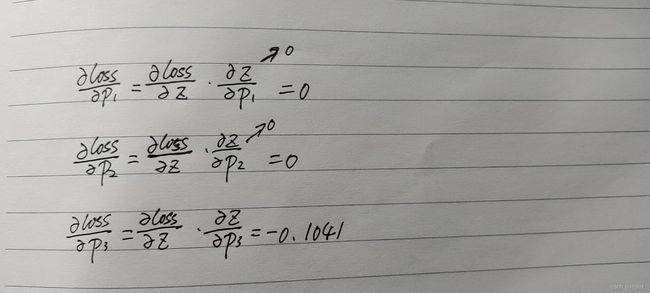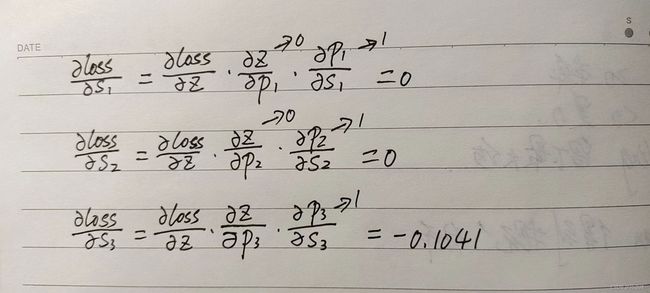2022.8.21 第二十次周报
目录
前言
关于卷积神经网络基础知识的了解
1.全连接神经网络概念
2.卷积神经网络基本概念
3.神经网络的优化方法
手推卷积神经网络CNN
Forword:
Backpropagation:
总结
前言
本次周报主要介绍神经网络的一些基本概念,包括全神经网络概念,卷积神经网络的组成和优化方法的概念和分类。除此之外,介绍了CNN的手推过程,这也是非常重要的一个部分。
关于卷积神经网络基础知识的了解
1.全连接神经网络概念
在学习卷积神经网络之前,我们先要明白什么是全神经网络?简单来说,全神经网络就是指对n-1层和n层而言,n-1层的任意一个节点,都和第n层所有节点有连接。
如果用全连接神经网络处理大尺寸图像具有三个明显的缺点:
(1)首先将图像展开为向量会丢失空间信息;
(2)其次参数过多效率低下,训练困难;
(3)同时大量的参数也很快会导致网络过拟合。
而使用卷积神经网络可以很好地解决上面的三个问题。
2.卷积神经网络基本概念
与常规神经网络不同,卷积神经网络的各层中的神经元是3维排列的:宽度、高度和深度。其中的宽度和高度是很好理解的,因为本身卷积就是一个二维模板,但是在卷积神经网络中的深度指的是激活数据体的第三个维度,而不是整个网络的深度,整个网络的深度指的是网络的层数。
卷积神经网络主要由这几类层构成:输入层、卷积层,ReLU层、池化(Pooling)层和全连接层(全连接层和常规神经网络中的一样)。通过将这些层叠加起来,就可以构建一个完整的卷积神经网络。在实际应用中往往将卷积层与ReLU层共同称之为卷积层,所以卷积层经过卷积操作也是要经过激活函数的。具体说来,卷积层和全连接层(CONV/FC)对输入执行变换操作的时候,不仅会用到激活函数,还会用到很多参数,即神经元的权值w和偏差b;而ReLU层和池化层则是进行一个固定不变的函数操作。卷积层和全连接层中的参数会随着梯度下降被训练,这样卷积神经网络计算出的分类评分就能和训练集中的每个图像的标签吻合了。
3.神经网络的优化方法
我们常用的优化方法是梯度下降法,那具体优化的意义是什么呢?
优化算法就是一种能够帮我们最小化或者最大化目标函数(有时候也叫损失函数)的一类算法。而目标函数往往是模型参数和数据的数学组合。例如给定数据X和其对应的标签Y,我们构建的模型是一个线性模型,有了模型后,根据输入x就可以得到预测输出f(x),并且可以计算出预测值和真实值之间的差距,这个就是损失函数。我们的目的是找到合适的W, b时上述的损失函数的值达到最小,损失值越小,则说明我们的模型越接近于真实情况.
通过上面的描述可以知道,模型的内参(W, b)在模型中扮演着非常重要的角色,而这些内参的更新和优化就用到我们所说的优化算法,所以优化算法也层出不穷,而一个好的优化算法往往能够更加高效、更加准确的训练模型的内参。
我们在了解优化方法的基本概念以后,来学习一下优化方法的分类:
一般的,根据优化算法在优化过程中使用的导数阶数。可以将优化算法可以分为两大类,一阶优化算法和二阶优化算法。
一阶优化算法是指使用参数梯度值来最小化或者最大化损失函数的优化算法。
最为广泛应用的就是梯度下降法,参数的一阶导能够清晰的告诉我们损失函数在某个特定点上是增加的还是减少的。那什么是梯度呢?简而言之,梯度就是函数输出关于输的偏导数,只不过这里的输入和输出并不是简单的数值,而是向量。梯度与导数的区别就是导数是单个变量的,而梯度是多个变量的。梯度往往采用雅克比矩阵(Jacobian Matrix)进行表达。
二阶优化算法顾名思义,二阶优化算法就是采用二阶导数进行优化算法。二阶导数,有时候也被成为海森矩阵(Hessian)。因为二阶导数要求两次导数,尤其是在矩阵中进行求导,运算量会非常的大,所以二阶优化算法被用的比较少。
手推卷积神经网络CNN
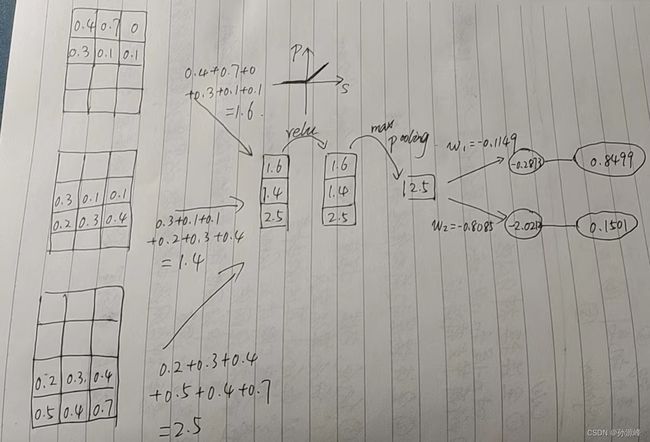
要优化的参数一共有八个,分别是filter上的六个参数和w1、w2,我们如下图初始化。
如图所示,filter上的六个参数都为1,w1=-0.1149,w2=-0.8085。
Forword:
我们首先将convolution的4*3的输入和2*3的backgroundfilter进行卷积。卷积的过程就是在矩阵x中取与矩阵U一样大小区域进行点对点乘,然后从左到右,从上到下按Z字形滑动,重复进行上述操作至结束,再把得到3 * 1矩阵S的结果进行Relu得到3 * 1的矩阵P,对P做maxpooling得到1 * 1的结果,然后再进行softmax。其中Relu的图像表示大于零的值是它本身,小于零的数是零;maxpooling是指选取最大的值。
Backpropagation:
step1:loss对o1,o2求导
step2:loss对w1,w2求导
step3:loss对z求导
step4:算梯度,loss对p1,p2,p3求导
step5:loss对s1,s2,s3求导
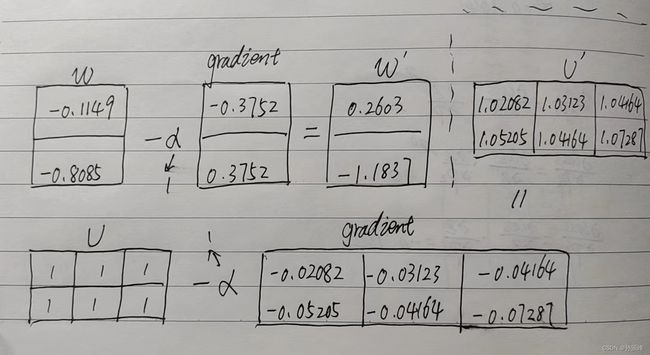
step6:计算卷积层的导数
step7:进行参数更新
总结
虽然说本周对神经网络有了一些简单的介绍,但是感觉对于整个卷积神经网络的结构还不是很清楚。下周将继续深度学习卷积神经网络的内容。包括卷积神经网络的结构,层的排列规律,卷积层的大小以及残差网络ResNet的了解。