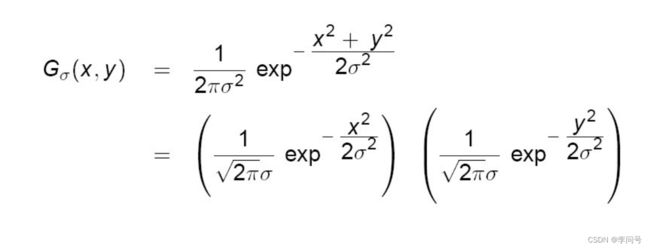卷积的概念,快速掌握卷积操作和高斯函数
卷积(Convolutions)
目录
- 卷积(Convolutions)
-
- (一)图像类型
-
- 1.二进制图像(Binary)
- 2.灰度图像(Gray Scale)
- 3.彩色图像(Color)
- (二)卷积操作
-
- 1.卷积核
- 2.卷积操作
- 3.性质
- 4.类型
- (三)图像填充
-
- 1.思想
- 2.方法
- (四)高斯函数(Gaussian Kernel)
-
- 1.要求
- 2.标准差σ
- 3.窗口大小
- 4.两者默认关系
- (五)噪声
-
- 1.高斯噪声
- 2.椒盐噪声(Salt and pepper noise)
- 3.脉冲噪声(Impulse noise)
- (六)中值滤波(Median filter)
-
- 1.计算方法
- 2.中值滤波器vs高斯滤波器
卷积贯穿着很多计算机视觉的任务,包括现在热门的深度学习网络——卷积神经网络。
在这篇文章中,主要介绍卷积的线性操作,通过理解卷积在图像去噪的应用,引出高斯函数,深入理解卷积。
(一)图像类型
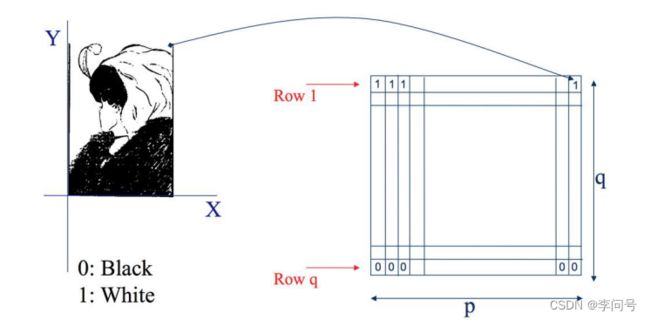
1.二进制图像(Binary)
在一个分辨率为p×q(宽度×高度)的图像中,每一个元素由0和1表示,要么是0(黑色),要么是1(白色),每一个点占1bit。
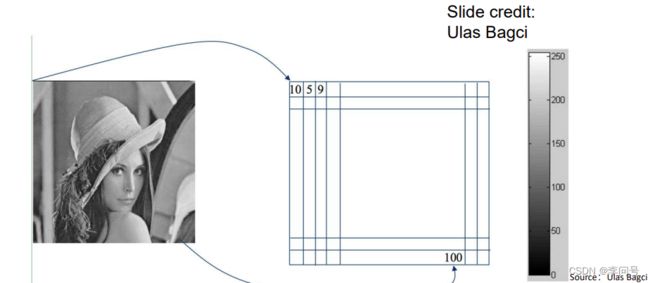
2.灰度图像(Gray Scale)
在一个分辨率为p×q的图像中,每个像素点的取值有256种,每一个点占1byte
3.彩色图像(Color)
在一个分辨率为p×q的图像中,一个点有三个通道,分别是R、G、B,每个通道上元素的取值有256种,因此每个点用3byte表示。

(二)卷积操作
1.卷积核
噪声点:比周围的像素点较突兀的点。
如何去除噪声点,让图像效果更加平滑?
去除噪声点的一种最直接的思想就是把该点和周围的点平均一下,用周围点和该点的加权平均值作为该点的值
带权值的点构成的窗口称为卷积核,也称为滤波核。我们通过卷积核可以得知周围每个点的权重是多少。
卷积核模板的大小一般是奇数的,3×3、5×5、7×7。
具体是如何做的呢?
2.卷积操作
假设现在有一个图像f和一个卷积核g。
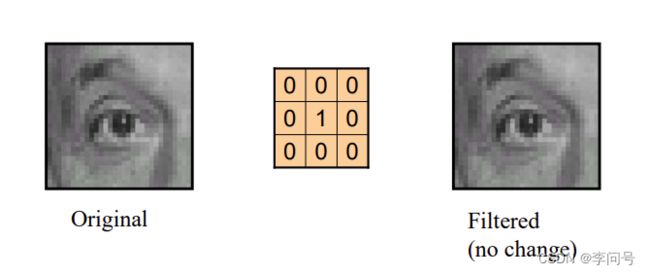
(1)首先,卷积核需要进行翻转(图像上的卷积核已经完成了翻转)
(2)经过翻转后的卷积核放置图像的左上方,从左上方开始对像素点进行运算。
(3)卷积后的图像上一点的值等于将卷积核模板的值(卷积核的中心点对应图像该点的位置)和对应位置的图像上点的值相乘后累加得到的值,这就是一个点的卷积操作的全过程。
(4)对于整个图像的卷积操作就是将卷积核平移,让每个点都进行一次卷积操作。
解释公式各符号的含义:
k,l的取值有-1、0、1;
[m,n]为卷积核的中心点在图像上的坐标;
f[x,y]为该点的图像的像素值;m-k与n-l实现卷积核的翻转;
g[x,y]为该点的卷积核的值,g[0,0]为卷积核的中心点的值。
3.性质
(1)线性
f1,f2两张图像,先求和再卷积与每张图像卷积之后再求和是一样的。
(2)平移不变性
先对图像平移再卷积与先对图像卷积再平移是一样的,因为卷积操作是对周围小邻域进行操作,平移并没有改变周围点的值。
推导出结论:任何平移不变的操作都可以用卷积操作
(3)其它的性质
4.类型
去噪:该点和周围的点平均后,整个图像就没有那么突兀了,所以就显得很模糊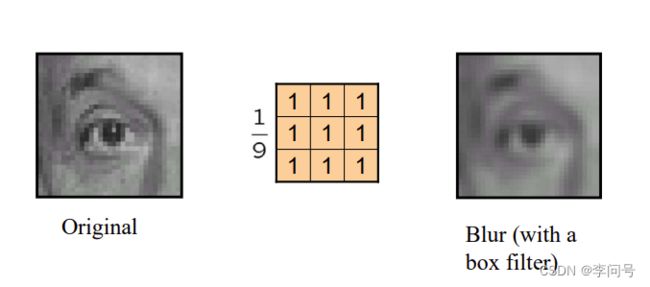
(4)锐化:棱角更加分明

锐化的原理:
(三)图像填充
对图像边缘进行卷积
对图像的边缘进行卷积时,卷积核的点并没有全部在图像里面,所以在真实运算时,我们就算不了图像边缘的值。
如何对图像边缘进行卷积?
1.思想
(1)如果要保证卷积的图像和原图像一样大,就要将图像扩大一圈,填充后卷积核的每个点都存在了对应位置的像素值
(2)如果不填充,卷积的图像就比原来的图像小一圈。
所以图像填充可以让输入和和经过卷积后的输出有一个固定的大小,防止多处理几次卷积后图像就没了。
2.方法
(1)clip filter(black)
最常用的方法就是给边缘的周围都补上0,这种方法在深度学习的卷积神经网络常用。但由于填充的是0,边缘周围和0进行平均都会接近于黑色
(2)wrap aroud
园筒状,把图片绕成一个环状。
(3)copy edge
直接把图像边缘的像素拉伸
(4)reflect across edge
填充边缘的镜像
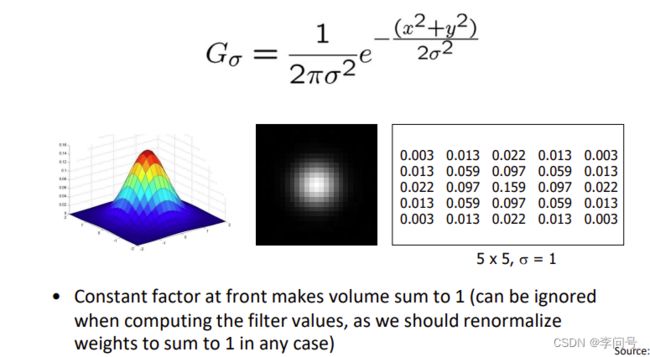
(四)高斯函数(Gaussian Kernel)
如果卷积核模板每个点的值是一样的,卷积核是个方形,就会产生振铃效果
振铃效果:即卷积后的图像种存在一些不像原图的纹理。
因此,我们必须避免振铃效果的产生。
使用高斯函数。
使卷积核越靠近中心点权重最高,越远离中心点权重越小
1.要求
(1)要求卷积核模板所有的权重之和为1。
高斯函数构成的图像的面积为1
设想如果卷积核的所有点的值相加不等于0,比如一个灰度图像的所有点的值都是255,去噪后该图像的值应该保持不变,但是如果33卷积核的每个点的值都是0.1(相加为0.9),经过滤波后,图像上每个点的值为2550.9。
(2)卷积核的窗口大小是5×5且σ的值为1,这两个值是指定的。
有了这两个值之后才可以计算卷积核每个点的值
(3)计算完之后,要对所有的值进行归一化。
比如在上图中,实际卷积核某点的值=(G/G1+G2+…+Gn)* 1/5*5。

分解前,图像每一个点计算的复杂度O( m 2 {m^2} m2),整个图像的复杂度就是( n 2 m 2 {n^2m^2} n2m2)
分解后,m×m的卷积核变成1×m和m×1两个,那么每一个点计算的复杂度是O(m+m),整个图像的复杂度就是( n 2 m {n^2m} n2m)
(4)用方差为σ的高斯核进行两次卷积,与用方差为√2σ的核进行一次卷积是一样的。
用标准差为σ的高斯核进行两次卷积来取代用方差为√2σ的核进行一次卷积,复杂度更低,计算更快
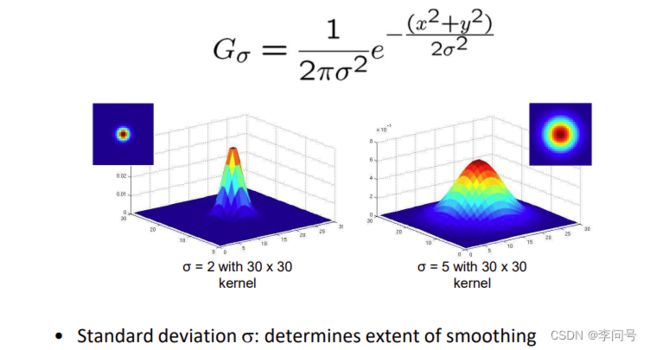
2.标准差σ
等于方差(每个样本值与全体样本值的平均数之差的平方值的平均数)的算数平方根
(1)σ越小表示数据越集中,图像呈现出来越细长—>窗口大小一定,σ越小中间点的权重越大,滤波后平滑的效果弱
(2)σ越大图像越扁—>窗口大小一定,σ越大中间点的权重越小,滤波后平滑的效果强,图像越模糊
3.窗口大小
(1)窗口越大,归一化时分母越大,靠近中心的点的权重越小,滤波后平滑的越厉害
(2)窗口越小,归一化时分母越小,靠近中心的点的权重越大,滤波后平滑结果就没那么明显
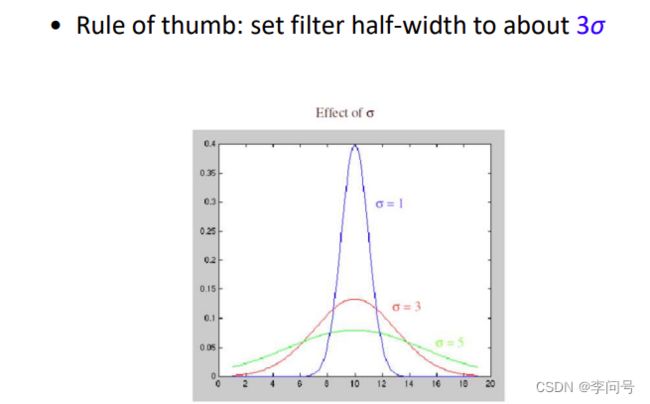
4.两者默认关系
窗口大小=3σ×2+1
如果σ=1,窗口大小设置为7×7
如果σ=2,窗口大小设置为13×13
值得一提的是,在计算机视觉中卷积和高斯贯穿始终,高斯一旦放在卷积里,就可以拓展出好多东西,包括卷积神经网络。
(五)噪声
1.高斯噪声
(高斯噪声)
(1)图像上一点的实际值等于该点像素值+高斯噪声(随机采样出来的值)
(2)不同噪声点之间相互独立,互不影响
(3)用高斯滤波器解决高斯噪声的问题
高斯噪声比较小,高斯滤波器的标准差小的就可以去噪;
高斯噪声比较大,高斯滤波器的标准差也要变大才能很好的去噪。
如下图所示,可以得出去噪效果在高斯噪声标准差比较小的时候有效(上方的σ为高斯噪声的标准差,右方的σ为高斯滤波器的标准差
2.椒盐噪声(Salt and pepper noise)
3.脉冲噪声(Impulse noise)
这两种噪声点的产生是随机的,就是突然出现一个白点或黑点,把原来的像素点覆盖。
用高斯滤波器并不能很好的去噪
使用中值滤波器
(六)中值滤波(Median filter)
相比高斯滤波器模板,中值滤波器模板没有权值,那如何计算呢?
1.计算方法
将图像的像素点的值从小到大排序,选择中间的点作为该点滤波后的值
中值滤波没有产生新的像素值
2.中值滤波器vs高斯滤波器
(1)高斯滤波是线性操作,中值滤波不是线性操作
(2)随着窗口增大,高斯滤波后的图像越来越模糊,如果中值滤波器的窗口变大,在更大范围的值之间去选择新的图像上该点的值,也会导致图像变模糊
(3)输入中存在间隔较大的点时,中值滤波不受影响,而高斯滤波会受到影响。