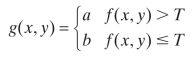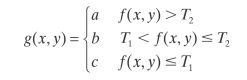图像的阈值处理

一般情况下，一张图片分为前景和背景，我们感兴趣的一般的是前景部分，所以我们一般使用阈值将前景和背景分割开来，使我们感兴趣的图像的像素值为1，不感兴趣的我0，有时一张图我们会有几个不同的感兴趣区域（不在同一个灰度区域），这时我们可以用多个阈值进行分割，这就是阈值处理。

单个阈值：

两个阈值：

示意图如下：

1.基本全局阈值处理

一般选取阈值就是图像直方图的视觉检测。将区分度大的两个灰度级部分之间进行划分，取T为阈值来分开它们。在此基础上学习一种自动地选择阈值的算法，方法如下：

针对全局阈值选择初始估计值T；

用T分割图像，G1是所有灰度值大于T的像素组成，G2是所有灰度值小于等于T的像素组成；

分别计算G1和G2区域内的平均灰度值m1和m2；

计算出新的阈值，取他们的m1和m2平均值数；

重复步骤2.-4.，直到在连续的重复中，T的差异比预先设定的参数小为止；

使用函数im2bw分割图像：g = im2bw(f,T/den)

代码如下：

clc        %清除命令窗口的内容
close all  %关闭所有的Figure窗口
clear all  %清除工作空间的所有变量


origin_ima=imread('Fig.tif');
hist1=imhist(origin_ima);
[seg_ima,T]=Global_threshold(origin_ima,2);
hist2=imhist(seg_ima);

subplot(2,2,1);imshow(origin_ima);title('原图像');
subplot(2,2,2);stem(hist1,'.');title('原图直方图');
subplot(2,2,3);imshow(seg_ima);title('全局分割图像');
subplot(2,2,4);stem(hist2,'.');title('全局分割图像直方图');

uint8(T)


%% 全局阈值分割函数，det_T0为迭代控制参数
function [Result,T0] = Global_threshold(ima,det_T0)
[m,n]=size(ima);
Result = zeros(m,n);

value=0;
for x=1:m
    for y=1:n
        value=value+double(ima(x,y));
    end
end
T0=value/(m*n); det_T = T0;

while(det_T>det_T0)
    G1=0;G2=0;count1=0;count2=0;
    for x=1:m
        for y=1:n
            if(ima(x,y)>T0)
                G1=G1+double(ima(x,y));
                count1=count1+1;
            else
                G2=G2+double(ima(x,y));
                count2=count2+1;
            end
        end
    end
    m1=G1/count1; m2=G2/count2;
    T=1/2*(m1+m2);
    det_T=T-T0; T0=T;
end


for x=1:m
   for y=1:n
        if(ima(x,y)>T0)
            Result(x,y)=1;
        end
   end
end
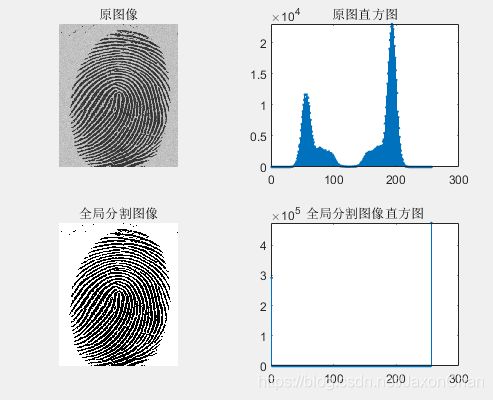
end

实验结果：  

        本实验是全局阈值是指整幅图像使用同一个阈值做分割处理，适用于背景和前景有明显对比的图像。它是根据整幅图像确定的：T=T(f)。但是这种方法只考虑像素本身的灰度值，一般不考虑空间特征，因而对噪声很敏感。从图可以看出，经处理的图像所处的位置以偏离原先位置。虽然两者处理显示的图像形状虽然一致，但是目标图像所在的位置不一致，自动全局阈值化的结果与原始图像一致，而最优阈值化处理结果偏离原始图像。可以看出经阈值处理的图像更加清晰，物体和背景间的分割相当有效。

2.使用Otsu’s方法的最佳全局阈值处理

Otsu’s方法的最佳方法是选择阈值k,最大类间方差σ2(k)来定义的：

当设置的方差越大，则完全分割一幅图像的阈值就会越接近。公式中的k就是我们所要寻找的最佳阈值，当k不唯一时，则将所有的最佳阈值进行取平均值即可。

代码如下：

clc        %清除命令窗口的内容
close all  %关闭所有的Figure窗口
clear all  %清除工作空间的所有变量

origin_ima=imread('Fig.tif');
hist1=imhist(origin_ima);

p=Histogram(origin_ima);
[seg_ima1,T]=Global_threshold(origin_ima,2);

[seg_ima,T] = Optimal_threshold(origin_ima,p);
hist2=imhist(seg_ima);

subplot(2,2,1);imshow(origin_ima);title('原图像');
subplot(2,2,2);stem(hist1,'.');title('原图直方图');
subplot(2,2,3);imshow(seg_ima1);title('全局分割图像');
subplot(2,2,4);imshow(seg_ima);title('Otsu方法分割图像');

T



%% 计算图像概率直方图
function p = Histogram(ima)
[m,n]=size(ima);
p=zeros(256,1);
for x=1:m
    for y=1:n
        p(ima(x,y)+1)=double( p(ima(x,y)+1)+1 );
    end
end
p=p/(m*n);
end

%% 进行最优阈值分割，输入原图像和概率直方图，返回分割图像和最优阈值
function [seg_ima,T] = Optimal_threshold(ima,p)

mG=0;
for k=0:255
    mG = mG + k*p(k+1);
end

P1=zeros(256,1);
for k=0:255
    for j=0:k
        P1(k+1) = P1(k+1)+p(j+1);
    end
end

m=zeros(256,1);
for k=0:255
    for j=0:k
        m(k+1) = m(k+1)+j*p(j+1);
    end
end

var=zeros(256,1);
for k=1:256
    var(k) = ( mG*P1(k)-m(k) )^2 / ( P1(k)*(1-P1(k)));
end
    
max=0;count=0;T=0;
for k=1:256
    if(var(k))>max
        max=var(k);
    end
end

for k=1:256
    if(var(k))==max
        count=count+1;
        T=T+k-1;
    end
end
T=T/count;

[a,b]=size(ima);
seg_ima=zeros(256);
for x=1:a
    for y=1:b
        if(ima(x,y)>T)
            seg_ima(x,y)=1;
        end
    end
end
end

%% 全局阈值分割函数，det_T0为迭代控制参数
function [Result,T0] = Global_threshold(ima,det_T0)
[m,n]=size(ima);
Result = zeros(m,n);

value=0;
for x=1:m
    for y=1:n
        value=value+double(ima(x,y));
    end
end
T0=value/(m*n); det_T = T0;

while(det_T>det_T0)
    G1=0;G2=0;count1=0;count2=0;
    for x=1:m
        for y=1:n
            if(ima(x,y)>T0)
                G1=G1+double(ima(x,y));
                count1=count1+1;
            else
                G2=G2+double(ima(x,y));
                count2=count2+1;
            end
        end
    end
    m1=G1/count1; m2=G2/count2;
    T=1/2*(m1+m2);
    det_T=T-T0; T0=T;
end

for x=1:m
   for y=1:n
        if(ima(x,y)>T0)
            Result(x,y)=1;
        end
   end
end
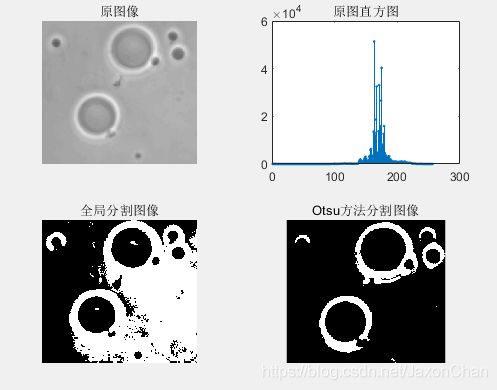
end

实验结果： 

        Otsu’s方法的最佳方法是选择阈值k,当设置的方差越大，则完全分割一幅图像的阈值就会越接近。公式中的k就是我们所要寻找的最佳阈值，当k不唯一时，则将所有的最佳阈值进行取平均值即可。

        可以看出，用基本全局阈值处理时细胞的分割效果并不是很好，没有能够分割清楚，是由于前景和背景的灰度级比较相近而不能够完全分离开，因此当使用了Otsu算法进行分割时，可以完全将前景和背景分割开来。尽管分离度的度量值比较低，但是还是可以准确地从背景中提取细胞。