Mr_LeeCZ

Bishop 模式识别与机器学习读书笔记_ch3.1 线性回归(I)

ch3.1 线性回归(I)

文章目录

ch3.1 线性回归(I)

@[toc]

1. 线性回归问题

1.1 聊聊模型的假设

1.2 假设的内涵性

1.3 假设的简化性

1.4 假设的发散性

2. 一元线性回归

2.1 极小均方误差

2.2 参数估计

2.3 模型的评估

2.4 从统计学角度看线性回归

2.5 似然函数

3. 多元线性回归

3.1 问题的来源

3.2 参数估计

4. 线性基函数回归模型

4.1 线性基函数回归

4.2 基函数

4.3 似然函数

4.4 参数估计

5. 代码实现

5.1 Toy Dataset

5.2 Real Dataset

1. 线性回归问题

1.1 聊聊模型的假设

机器学习中的建模过程，往往充斥着假设，合理的假设是合理模型的必要前提。
假设具有三个性质：
- 内涵性
- 简化性
- 发散性

1.2 假设的内涵性

所谓假设，就是根据常理应该是正确的。

如假定一个人的身高位于区间 $[150 c m, 220 c m]$ ，这能够使得大多数情况都是对的，但很显然有些篮球运动员已经不属于这个区间。所以，假设的第一个性质：假设往往是正确的但不一定总是正确。
我们可以称之为“假设的内涵性”。

1.3 假设的简化性

假设只是接近真实，往往需要做若干简化。

如，在自然语言处理中，往往使用词袋模型(Bag Of Words)，认为一篇文档的词是独立的——这样的好处是计算该文档的似然概率非常简洁，只需要每个词出现概率乘积即可。
但我们知道这个假设是错的：一个文档前一个词是“正态”，则下一个词极有可能是“分布”，文档的词并非真的独立。
这个现象可以称之为“假设的简化性”。

1.4 假设的发散性

在某个简化的假设下推导得到的结论，不一定只有在假设成立时结论才成立。

如，我们假定文本中的词是独立的，通过朴素贝叶斯做分类(如垃圾邮件的判定)。
我们发现：即使使用这样明显不正确的假设，但它的分类效果往往在实践中是堪用的。
这个现象可以称之为“假设的发散性”。

2. 一元线性回归

已知一个一元数据集 ${(x_i,t_i)\}_{i=1}^n$ ，其中， $x_i\in R, t_i\in R$ 面对一个新的数据点 $x$ ，试计算其对应的 $t$ ，此问题成为预测问题
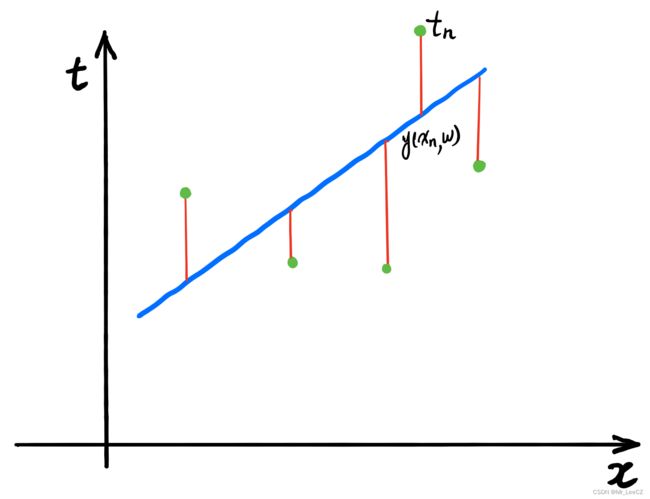
问题的本质：寻找一个合适的线性函数 $y = w x + b$ ，使其均匀地穿过数据集

2.1 极小均方误差

均方误差（Squared Error, SE）可表示为：

$E(w,b)=\sum_{i=1}^m(t_i-y_i)^2=\sum_{i=1}^m(t_i-wx_i-b)^2$

极小均方误差(Minimize Squared Error, MSE)可表示为：
$(\hat{w},\hat{b})=\arg\min_{(w,b)}\sum_{i=1}^m(t_i-wx_i-b)^2$

2.2 参数估计

对函数 $E (w, b)$ 关于 $w$ 求偏导得：
$\begin{align*} \frac{\partial E(w,b)}{\partial w}&=\sum_{i=1}^m2(t_i-wx_i-b)\cdot(-x_i)\\ &=2w\sum_{i=1}^mx_i^2+2\sum_{i=1}^m(t_i-b)(-x_i)\\ &=2\Big(w\sum_{i=1}^mx_i^2-\sum_{i=1}^m(t_i-b)x_i\Big)\\ &=0 \end{align*}$
对函数 $E (w, b)$ 关于 $b$ 求偏导得：
$\begin{align*} \frac{\partial E(w,b)}{\partial b}&=\sum_{i=1}^m2(t_i-wx_i-b)\cdot(-1)\\ &=2\Big(mb-\sum_{i=1}^m(t_i-wx_i))\Big)\\ &=0 \end{align*}$
得：
$\hat{b}=\frac{1}{m}\sum_{i=1}^m(t_i-wx_i)$

将 $\hat{b}$ 代入 $\frac{\partial E(w,b)}{\partial w}$ 得：
$\begin{align} \frac{\partial E(w,b)}{\partial w}&=w\sum_{i=1}^mx_i^2-\sum_{i=1}^mt_ix_i+b\sum_{i=1}^mx_i \\ &=w\sum_{i=1}^mx_i^2-\sum_{i=1}^mt_ix_i+\frac{1}{m}\sum_{i=1}^m(t_i-wx_i)\sum_{i=1}^mx_i \\ &=w\sum_{i=1}^mx_i^2-\sum_{i=1}^mt_ix_i+\frac{1}{m}\sum_{i=1}^mt_i\sum_{i=1}^mx_i-\frac{w}{m}(\sum_{i=1}^mx_i) \\ &=w\Big(\sum_{i=1}^m-\frac{1}{m}(\sum_{i=1}^mx_i)^2\Big)-\Big(\sum_{i=1}^mt_i(x_i-\overline{x})\Big) \\ &=0 \end{align} \tag {1}$

由(1)式得：
$\hat{w}=\frac{\sum_{i=1}^my_i(x_i-\overline{x})}{\sum_{i=1}^mx_i^2-\frac{1}{m}(\sum_{i=1}^mx_i)^2}$

2.3 模型的评估

可决系数(可决系数越大拟合的效果越好，但有可能过拟合)：
$R^2=1-\frac{\sum_{i=1}^m(t_i-\hat{y}_i)^2}{\sum_{i=1}^m(\overline{t}-\hat{y}_i)^2}$
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Nq8ZxOrt-1666427117960)(Img/LinearRegression/RR.png)]

2.4 从统计学角度看线性回归

数据集 ${(x_i,t_i)\}_{i=1}^m$ ，其中 $x_i\in R, t_i\in R$ ，把 $x_i,t_i$ 看作随机变量，则有
$t_i=y_i+\varepsilon_i=wx_i+b+\varepsilon_i$
则 $\varepsilon_i$ 也是随机变量， $\varepsilon_i\sim N(0,\sigma^2)$
即
$t_i\sim N(wx_i+b,\sigma^2)$
也可是表示为：
$P(t_i|w,b,x_i,\sigma^2)\sim N(wx_i+b+\sigma^2)$

2.5 似然函数

$\boldsymbol{t}=\{t_i\}_{i=1}^m$ 出现的联合概率分布（假设 $x_i,\varepsilon$ 本别是相互独立的）为
$P(\boldsymbol{t}|w,b,X,\sigma^2)=\prod_{i=1}^m P(t_i|w,b,x_i,\sigma^2)$
则Log似然可表示为：
$\ln P(\boldsymbol{t}|w,b,X,\sigma^2)=-0.5n\ln(2\pi\sigma^2)-\frac{1}{2\sigma^2}\sum_{i=1}^m(t_i-wx_i-b)^2$
则极大Log似然估计为：
$(\hat{w},\hat{b})=\arg\max_{w,b}\ln P(T|w,b,X,\sigma^2)=\arg\min_{w,b}\sum_{i=1}^m(t_i-wx_i-b)^2$

这与极小均方误差(MSE)是一致的

3. 多元线性回归

3.1 问题的来源

数据集 $\{(\boldsymbol{x}_i,t_i)\}_{i=1}^m$ ，其中， $\boldsymbol{x}_i \in R^d, t_i\in R$
则有：
$t_i=y_i+\varepsilon_i$
多元线性函数可表示为：
$t_i=ax_{i1}+a_2x_{i2}+\cdots+a_dx_{id}+b+\varepsilon_i=\boldsymbol{w}^T\boldsymbol{x}_i+b+\varepsilon_i$

其中 $\boldsymbol{w}=(a_1,a_2,\cdots,a_d)^T, \boldsymbol{x}_i=(x_{i1},x_{i2},\cdots,x_{id})^T$

令
$\boldsymbol{\widetilde{X}} = \left[ \begin{matrix} x_{11} & x_{12} & \cdots &x_{1d} & 1 \\ x_{21} & x_{22} & \cdots &x_{2d} & 1 \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ x_{m1} & x_{m2} & \cdots &x_{md} & 1 \\ \end{matrix} \right]$

令
$\boldsymbol{\widetilde{w}}=(\boldsymbol{w},b)^T$

拟合函数可记为
$\boldsymbol{y}=f(\boldsymbol{\widetilde{X}})=\boldsymbol{\widetilde{X}}\boldsymbol{\widetilde{w}}$
则有
$\boldsymbol{t}=f(\boldsymbol{\widetilde{X}})+\epsilon=\boldsymbol{\widetilde{X}}\boldsymbol{\widetilde{w}}+\epsilon$
其中， $\epsilon=(\varepsilon_1,\varepsilon_2,\cdots,\varepsilon_m)^T$

根据极小化均方误差（MSE）原则，目标函数可表示为
$\boldsymbol{\widetilde{w}}^*=\arg\min_{\boldsymbol{\widetilde{w}}}(\boldsymbol{t}-\boldsymbol{\widetilde{X}}\boldsymbol{\widetilde{w}})^T(\boldsymbol{t}-\boldsymbol{\widetilde{X}}\boldsymbol{\widetilde{w}})$

3.2 参数估计

目标函数可记为：
$E(\boldsymbol{\widetilde{w}})=(\boldsymbol{t}-\boldsymbol{\widetilde{X}}\boldsymbol{\widetilde{w}})^T(\boldsymbol{t}-\boldsymbol{\widetilde{X}}\boldsymbol{\widetilde{w}})$
对目标函数 $E(\boldsymbol{\widetilde{w}})$ 关于 $\boldsymbol{\widetilde{w}}$ 求偏导数得
$\frac{\partial{E(\boldsymbol{\widetilde{w}})}}{\partial \boldsymbol{\widetilde{w}}}=-2\boldsymbol{\widetilde{X}}^T(\boldsymbol{\widetilde{X}}\boldsymbol{\widetilde{w}}-\boldsymbol{t})=\boldsymbol{0}$
$\boldsymbol{\widetilde{w}}$ 的估计值可表示为
$\boldsymbol{\widetilde{w}}^*=(\boldsymbol{\widetilde{X}}^T\widetilde{X})^{-1}\boldsymbol{\widetilde{X}}^T\boldsymbol{t}$
则线性回归模型可表示为
$y=f(\boldsymbol{x})=\boldsymbol{\widetilde{x}}^T(\boldsymbol{\widetilde{X}}^T\boldsymbol{\widetilde{X}})^{-1}\boldsymbol{\widetilde{X}}^T\boldsymbol{t}$

4. 线性基函数回归模型

4.1 线性基函数回归

数据集 $\boldsymbol{x}=(x_1,x_2,\cdots,x_d)^T$ ，线性回归函数为
$y(\boldsymbol{x},\boldsymbol{w})=w_0+w_1x_1+\cdots+w_dx_d$
令 $\phi_j(\boldsymbol{x})$ 表示为基函数，则线性回归基函数回归可表示为
$y(\boldsymbol{x},\boldsymbol{w})=w_0+\sum_{j=1}^dw_j\phi_j(\boldsymbol{x})$
增加虚拟基函数 $\phi_0(x)=1$ 则线性回归基函数回归可表示为
$y(\boldsymbol{x},\boldsymbol{w})=w_0+\sum_{j=1}^dw_j\phi_j(\boldsymbol{x})=\boldsymbol{w}^T\Phi(\boldsymbol{x})$
其中， $w=(w_0,w_1,w_2,\cdots,w_d)^T,\Phi=(\phi_0,\phi_1,\cdots,\phi_d)^T$

4.2 基函数

基函数可用如下两种种函数：

高斯基函数：

$\phi_j(x)=exp\Big\{-\frac{(x-\mu_j)^2}{2\sigma^2}\Big\}$

sigmoid 基函数：

$\phi_j(x)=S(\frac{x-\mu_j}{\sigma})$

其中，

$S(a)=\frac{1}{1+\exp(-a)}$

4.3 似然函数

由 $t=y(x,w)+\varepsilon$ 知
$p(t|\textbf{x},\textbf{w},\sigma)=N(t|y(\textbf{x},\textbf{w}),\sigma^2)$
极大似然函数表示为
$p(\textbf{t}|\textbf{X},\textbf{w},\sigma)=\prod_{j=1}^mN(t_n|\textbf{w}^T\phi(\textbf{x}_n),\sigma^2)$
Log似然函数函数
$\ln p(\textbf{t}|\textbf{X},\textbf{w},\sigma)=\sum_{j=1}^m\ln N(t_n|\textbf{w}^T\phi(\textbf{x}_n),\sigma^2)$
即
$\ln p(\textbf{t}|\textbf{X},\textbf{w},\sigma)=\frac{N}{2}\ln\sigma^{-2}-\frac{N}{2}\ln(2\pi)-\frac{1}{2\sigma^2}\sum_{j=1}^m\{t_j-\textbf{w}^T\phi(\textbf{x}_n)\}^2$

4.4 参数估计

求极值，设置导数为 $0$
$\begin{align} \bigtriangledown \ln p(\textbf{t}|w,\sigma)&=\sum_{j=1}^m\{t_n-\textbf{w}^T\phi(\textbf{x}_n)\}\phi(\textbf{x}_n)^T(-1) \\ &=\sum_{j=1}^m t_n\phi(\textbf{x}_n)^T-\textbf{w}^T\Big(\sum_{j=1}^m\phi(x_n)\phi(x_n)^T\Big) \\ &=\mathbf{0} \end{align}$
结果为：
$\textbf{w}_{ML}=(\Phi^T\Phi)^{-1}\Phi^T \textbf{t}$
其中
$\Phi= \left( \begin{matrix} \phi_0(\textbf{x}_1) & \phi_1(\textbf{x}_1) & \cdots & \phi_d(\textbf{x}_1)\\ \phi_0(\textbf{x}_2) & \phi_1(\textbf{x}_2) & \cdots & \phi_d(\textbf{x}_2)\\ \cdots & \cdots & \cdots & \cdots \\ \phi_0(\textbf{x}_m) & \phi_1(\textbf{x}_m) & \cdots & \phi_d(\textbf{x}_m)\\ \end{matrix} \right)$
多项式回归可看做多项式基函数所得结果

5. 代码实现

5.1 Toy Dataset

#!/usr/bin/python
# -*- coding:utf-8 -*-

import numpy as np
from sklearn.linear_model import LinearRegression, RidgeCV, LassoCV, ElasticNetCV
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
import matplotlib.pyplot as plt

np.random.seed(0)
N = 9
x = np.linspace(0, 6, N) + np.random.randn(N)
x = np.sort(x)
y = x**2 - 4*x - 3 + np.random.randn(N)

x.shape = -1, 1 # 把行向量转变为列向量
y.shape = -1, 1

model = Pipeline([('poly', PolynomialFeatures()),
                  ('linear', LinearRegression(fit_intercept=False))])

d_pool = np.arange(1,10,1)  # 阶


for d in d_pool:
    plt.subplot(3,3,d)
    plt.plot(x, y, 'ro', markersize=4, zorder=N, mec='k')
    model.set_params(poly__degree=d)
    model.fit(x, y.ravel())
    x_hat = np.linspace(x.min(), x.max(), num=100)
    x_hat.shape = -1, 1
    y_hat = model.predict(x_hat)
    plt.plot(x_hat, y_hat)


plt.show()

输出结果

5.2 Real Dataset

#!/usr/bin/python
# -*- coding:utf-8 -*-

import csv
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error
from pprint import pprint


if __name__ == "__main__":
    show = False
    path = 'data/Advertising.csv'

    # pandas读入
    data = pd.read_csv(path)    # TV、Radio、Newspaper、Sales
    # x = data[['TV', 'Radio', 'Newspaper']]
    x = data[['TV', 'Radio']]
    y = data['Sales']
    print('Persone Corr = \n', data.corr())
    print(x)
    print(y)
    print(x.shape, y.shape)

    mpl.rcParams['font.sans-serif'] = ['simHei']
    mpl.rcParams['axes.unicode_minus'] = False
    if show:
        # 绘制1
        plt.figure(facecolor='white')
        plt.plot(data['TV'], y, 'ro', label='TV', mec='k')
        plt.plot(data['Radio'], y, 'g^', mec='k', label='Radio')
        plt.plot(data['Newspaper'], y, 'mv', mec='k', label='Newspaer')
        plt.legend(loc='lower right')
        plt.xlabel('广告花费', fontsize=16)
        plt.ylabel('销售额', fontsize=16)
        plt.title('广告花费与销售额对比数据', fontsize=18)
        plt.grid(b=True, ls=':')
        plt.show()

        # 绘制2
        plt.figure(facecolor='w', figsize=(9, 10))
        plt.subplot(311)
        plt.plot(data['TV'], y, 'ro', mec='k')
        plt.title('TV')
        plt.grid(b=True, ls=':')
        plt.subplot(312)
        plt.plot(data['Radio'], y, 'g^', mec='k')
        plt.title('Radio')
        plt.grid(b=True, ls=':')
        plt.subplot(313)
        plt.plot(data['Newspaper'], y, 'b*', mec='k')
        plt.title('Newspaper')
        plt.grid(b=True, ls=':')
        plt.tight_layout(pad=2)
        # plt.savefig('three_graph.png')
        plt.show()

    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=1)
    model = LinearRegression()
    model.fit(x_train, y_train)
    print(model.coef_, model.intercept_)

    order = y_test.argsort(axis=0)
    y_test = y_test.values[order]
    x_test = x_test.values[order, :]
    y_test_pred = model.predict(x_test)
    mse = np.mean((y_test_pred - np.array(y_test)) ** 2)  # Mean Squared Error
    rmse = np.sqrt(mse)  # Root Mean Squared Error
    mse_sys = mean_squared_error(y_test, y_test_pred)
    print('MSE = ', mse, end=' ')
    print('MSE(System Function) = ', mse_sys, end=' ')
    print('MAE = ', mean_absolute_error(y_test, y_test_pred))
    print('RMSE = ', rmse)
    print('Training R2 = ', model.score(x_train, y_train))
    print('Test R2 = ', model.score(x_test, y_test))

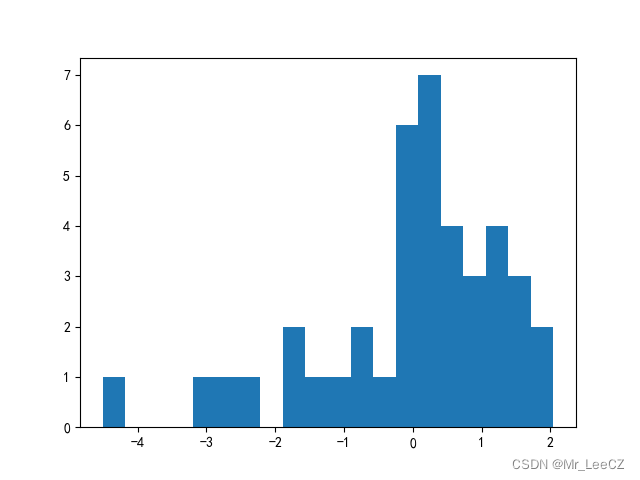
    error = y_test - y_test_pred
    np.set_printoptions(suppress=True)
    print('error = ', error)
    plt.hist(error, bins=20)
    plt.show()

    plt.figure(facecolor='w')
    t = np.arange(len(x_test))
    plt.plot(t, y_test, 'r-', linewidth=2, label='真实数据')
    plt.plot(t, y_test_pred, 'g-', linewidth=2, label='预测数据')
    plt.legend(loc='upper left')
    plt.title('线性回归预测销量', fontsize=18)
    plt.grid(b=True, ls=':')
    plt.show()