R语言-回归系数的极大似然估计
老师要求我们对回归方程中的回归系数进行极大似然估计,回归方程如下:
![]()
计算步骤如下:
步骤一:写出似然函数log(β),其中的β为 ( β 0 , β 1 , β 2 ) t (β_0, β_1, β_2)^t (β0,β1,β2)t
步骤二:解出log’(β)=0的根
由回归分析的知识, y i y_i yi ~ N ( β 0 + β 1 x 1 i + β 2 x 2 i , 1 ) N( \beta_0 +\beta_1x_{1i}+\beta_2x_{2i},1) N(β0+β1x1i+β2x2i,1)
因此可以写出似然函数:

取对数

其中C为常数
但是在写代码的时候不用将极大似然函数表示出来,只需要对log’(β)=0求根即可,这里用的是牛顿法求根。
首先来简单介绍一下牛顿算法:
这是一种通过不断迭代来求根的算法,先随便给一个初始的x值,再给出迭代原则,最终就能找到方程的根。例如图中是求 g ( x ) = 3 x 5 − 4 x 4 + 6 x 3 + 4 x − 4 g(x)=3x^5-4x^4+6x^3+4x-4 g(x)=3x5−4x4+6x3+4x−4的根,通过三次迭代就可以很接近了。

图中展现的是一维牛顿迭代,从几何上易知:

从而推出
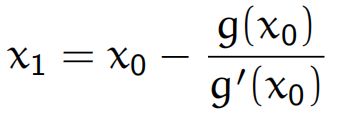
注意在我们的优化算法中g(x)实际上是f(x)的导数,因此一维牛顿迭代的公式为
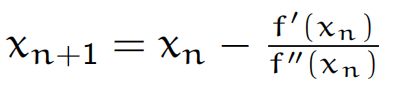
现在把它推广到高维牛顿迭代:
β n + 1 = β n − H − 1 G β_{n+1} = β_n - H^{-1} G βn+1=βn−H−1G
G为梯度矩阵,即一阶导矩阵

用牛顿迭代时,我们应该设置一个迭代停止的条件,不然程序会在零点附近永远运行下去。这里列出了一些可行的条件:
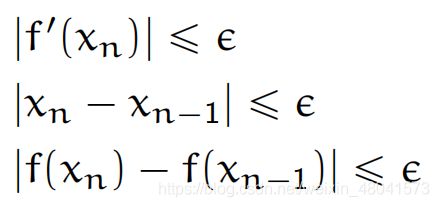
我设置的条件是 β n + 1 − β n < 0.0001 \beta_{n+1}-\beta_n < 0.0001 βn+1−βn<0.0001
整个过程用R语言来实现:
#生成数据集
#y是n*1的矩阵,b是[b0,b1,b2],x是n*3的矩阵
set.seed(2)
bbb0 = c(10,10,10)
y = 10 + 10*rnorm(10, 1, 1)
x1 = c(rep(1,10))
x2 = y*2 + rnorm(10,0,1)
x3 = y - 5 + rnorm(10,0,1)
x = t(rbind(x1, x2, x3))
#梯度矩阵
G = matrix(nrow = length(y), ncol = length(bbb0))
gloglike = function(b,y,x){
for (i in 1:length(y)) {
ei = y[i] - x[i,]%*%b #是一个数
ei = as.vector(ei)
gi = ei * x[i,] #1*3的矩阵
G[i,]=gi
}
return(colSums(G))
}
#黑塞矩阵
H = matrix(0, nrow = length(bbb0), ncol = length(bbb0))
Hloglike = function(x){
for (i in 1:length(y)) {
xi = as.matrix(x[i,])
h = -xi%*%t(xi)
H = H + h
#hi = as.vector(h)
#H[i,]=hi
}
#out = matrix(colSums(H))
#return(out)
return(H)
}
#牛顿求根算法
newton = function(x,y,bbb0){
HH = Hloglike(x)
GG = gloglike(bbb0,y,x)
delta = c(2,3,4)
n = 1
while (delta[1]>0.0001 || delta[2]>0.0001 || delta[3]>0.0001) {
bbb1 = bbb0 - solve(HH)%*%GG
delta = abs(bbb1 - bbb0)
bbb0 = bbb1
GG = gloglike(bbb0,y,x)
n = n + 1
}
result = list(bbb0,n)
return(result)
}
newton(x,y,bbb0)
最后结果为
x1 0.51256600
x2 0.46233262
x3 0.06147585
n = 3
x1,x2,x3 即为 β 0 , β 1 , β 2 β_0, β_1, β_2 β0,β1,β2 的估计结果,迭代次数为3次
