RNN学习2

---

前言

This week,I read an article and mainly learn about an approach mentioned in the article. The author uses Monte-Carlo dropout to develop an ensemble weather prediction system. Then I learn the related knowledge of RNN and master the formula of RNN forward and backward propagation. I implement the forward and backward propagation process with code.
本周阅读一篇文献，主要了解到这篇文献中所提到的一种方法， 采用蒙特卡罗 dropout集合预测。然后继续学习RNN的相关知识，掌握了RNN的正反向传播的公式，并用代码实现正反向传播的过程。

---

文献阅读

题目：A generative adversarial network approach to (ensemble) weather prediction
作者：Alex Bihlo

摘要

使用条件深度卷积生成对抗网络来预测欧洲上空 500 hPa 压力水平的地势高度、两米温度和未来 24 小时的总降水量。所提出的模型基于4年的ERA5再分析数据进行训练，目标是预测2019年的相关气象场。预报显示，地势高度和两米温度的真实再分析数据定性和定量吻合良好，但总降水量则不尽如人意，表明仅基于数据对特定气象参数进行天气预报是可能的。进一步使用蒙特卡罗dropout开发了一个纯基于深度学习策略的集成天气预报系统，并且通过允许量化模型学习的当前天气预报中的不确定性，进一步提高了预报模型的技能。

Monte-Carlo Dropout（蒙特卡罗 dropout）

深度学习中的两个不确定性：
1.偶然不确定性（数据不确定性）：由于观测数据本身的噪声产生的，比如人脸不清楚，标注框边缘不准确等，偶然不确定性是无法通过获取更多的观测数据来降低的。
2.认知不确定性（模型不确定性）：由于模型参数的不确定性、模型结构的不确定性产生的，即模型训练的不是很好，所以模型得出来的结果不是结果存在不确定性。
对于一个模型的输出结果，我们想得到这个结果的方差来计算模型不确定性。而模型的参数是固定的，一个单独输出值是得不到方差的，如果能够用同一个模型，对同一个样本进行T次预测，而且这T次的预测值各不相同，就能够计算方差。

同一个模型同一个样本，怎么得到不同的输出呢？可以让学到的模型参数不是确定的值，而是服从一个分布，那么模型参数就可以从这个分布中采样得到，每一次采样，得到的模型参数都是不同的，这样模型产生的结果也是不同的，我们的目的就达到了。

如何让模型的参数不是确定的而是服从一个分布呢？要在预测的时候，仍然将dropout打开，预测 T 次，取预测的平均值就是最终的预测值。并且通过平均值就可以得到方差，这样就得到深度学习的不确定性了。

采用蒙特卡罗 dropout的集合预测

对于所选的大气参数，运行了 100 个相应vid2vid模型的集合（分别对应500 hPa地势高度、两米温度和总降水量）。然后，根据这个结果集合，计算点集合均值和标准偏差分别为Zmean , Zstd。理想情况下，Zstd是衡量大气未来状态固有不确定性的指标，Z的值越高，在该区域大气发展的不确定性就越高。

结果

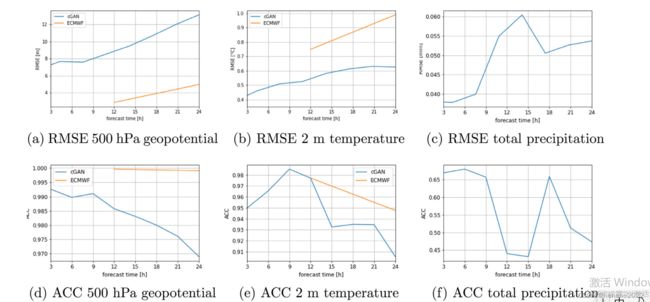RMSE 是衡量天气预报整体逐点准确性的标准指标，而 ACC 衡量的是预报预测异常情况相比与预报气候平均值的能力。好的天气预报的ACC为1，而值为0表示与使用气候学进行预报相比没有改善。一旦ACC低于0.6，由此产生的预测就不再具有实际价值。ACC对预测中的任何偏差都不敏感。
位势的结果是所有三个vid2vid结果中最好的，ACC在整体预测视图上接近于1。两米温度几乎与在ACC中测量的可靠性水平相同。在总降水量上结果最差，可能是由于数据分辨率不够高。

RNN循环神经网络

基础循环神经网络图

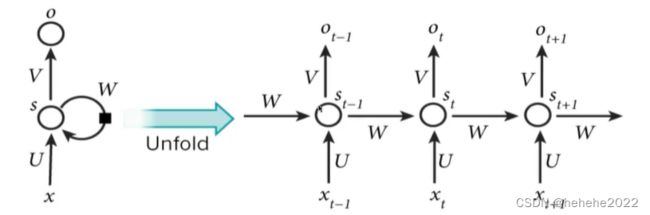
Xt表示每一个时刻的输入
Ot表示每一个时刻的输出
st表示每一个隐层的输出

所有单元的参数共享W\U\V

通用公式的表示：

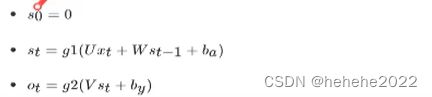
g1,g2：表示激活函数，g1:tanh/relu g2:sigmoid/softmax
矩阵运算表示
假设网络中某一时刻的公式为

假设有M个词，xt的长度为M，所以U的大小为NXM，N为输出S的维度，W的维度为NXN，V的维度为MXN。N是人为指定的一个长度，通常用来指定cell的状态输出的大小。

形状表示:[N,M]X[M,1]+[N,N]X[N,1]=[N,1]
此步骤可以简化为：[u,w]x[x/s]=[n,n+m]x[n+m,1]=[n,1]

交叉熵损失

总损失的定义：一整个序列（一个句子）作为一个训练实例，总误差就是各个时刻词的误差之和。
对于一个词损失计算为：Et(yt , ythat) = - yt log(ythat)
总损失：E(y , yhat)=∑t Et(yt , ythat) = - ∑t yt log(ythat)

时间反向传播算法（BPTT）

目标是优化参数，计算误差关于UVW以及两个偏置的梯度，用梯度下降更新参数。由于三组参数是共享的，要将一个训练实例在每一个时刻的梯度相加，加起来的梯度，为每次W更新的梯度值。

求不同参数的导数步骤：
区分最后一个cell和前面的cell的s的梯度值：

对最后一个cell：计算最后一个时刻的交叉熵损失E4对st的梯度，记为ds4，同理向前的每个损失对S求梯度，得到ds3,ds2,ds1，ds0。记忆交叉熵损失函数对于st,V，by的导数。

对于其余的cell： 求出当前层损失对于当前隐层状态输出值St的梯度(ds3)+上一层相对于st的损失（也就是ds4/ds3）。

计算tanh激活函数的导数。
计算Uxt + Wst-1 + ba对于不同参数的导数。

根据前向传播公式编写单个cell的前向传播过程，两个输入x_t, s_prev：

import numpy as np
from utils import *
def rnn_cell_forward(x_t, s_prev, parameters):
        """
        单个RNN-cell 的前向传播过程
        :param x_t: 当前T时刻单元的输入
        :param s_prev: 上一个单元的隐层状态输入
        :param parameters: 单元中的参数
        :return: s_next, out_pred, cache
        """

        # 获取参数
        U = parameters["U"]
        W = parameters["W"]
        V = parameters["V"]
        ba = parameters["ba"]
        by = parameters["by"]

        # 计算激活函数
        s_next = np.tanh(np.dot(U, x_t) + np.dot(W, s_prev) + ba)
        # 计算当前cell输出预测结果
        out_pred = softmax(np.dot(V, s_next) + by)

        # 存储当前单元的结果，方便反向传播计算
        cache = (s_next, s_prev, x_t, parameters)

        return s_next, out_pred, cache

所有cell的前向传播过程：

def rnn_forward(x, s0, parameters):
    """
    对多个Cell的RNN进行前向传播
    :param x: T个时刻的X总输入形状
    :param a0: 隐层第一次输入
    :param parameters: 参数
    :return: s, y, caches
    """
    # 初始化缓存
    caches = []

    # 根据X输入的形状确定cell的个数(3, 1, T)
    # m是词的个数，n为自定义数字：(3, 5)
    m, _, T = x.shape
    # 根据输出
    m, n = parameters["V"].shape

    # 初始化所有cell的S，用于保存所有cell的隐层结果
    # 初始化所有cell的输出y，保存所有输出结果
    s = np.zeros((n, 1, T))
    y = np.zeros((m, 1, T))

    # 初始化第一个输入s_0
    s_next = s0

    # 根据cell的个数循环,并保存每组的
    for t in range(T):
        # 更新每个隐层的输出计算结果，s,o,cache
        s_next, out_pred, cache = rnn_cell_forward(x[:, :, t], s_next, parameters)
        # 保存隐层的输出值s_next
        s[:, :, t] = s_next
        # 保存cell的预测值out_pred
        y[:, :, t] = out_pred
        # 保存每个cell缓存结果
        caches.append(cache)

    return s, y, caches

反向传播过程：
明确计算的梯度变量：
ds_next:表示当前cell的损失对输出st的导数
dtanh:表示当前cell的损失对激活函数的导数
dx_t:表示当前cell的损失对输入x_t的导数
dU:表示当前cell的损失对U的导数
ds_prev:表示当前cell的损失对上一个cell的输入的导数
dW:表示当前cell的损失对W的导数
dba:表示当前cell的损失对dba的导数

def rnn_cell_backward(ds_next, cache):
        """
        对单个cell进行反向传播
        :param ds_next: 当前隐层输出结果相对于损失的导数
        :param cache: 每个cell的缓存
        :return:
        """

        # 获取缓存值
        (s_next, s_prev, x_t, parameters) = cache
        print(type(parameters))

        # 获取参数
        U = parameters["U"]
        W = parameters["W"]
        V = parameters["V"]
        ba = parameters["ba"]
        by = parameters["by"]

        # 计算tanh的梯度通过对s_next
        dtanh = (1 - s_next ** 2) * ds_next

        # 计算U的梯度值
        dx_t = np.dot(U.T, dtanh)

        dU = np.dot(dtanh, x_t.T)

        # 计算W的梯度值
        ds_prev = np.dot(W.T, dtanh)
        dW = np.dot(dtanh, s_prev.T)

        # 计算b的梯度
        dba = np.sum(dtanh, axis=1, keepdims=1)

        # 梯度字典
        gradients = {"dx_t": dx_t, "ds_prev": ds_prev, "dU": dU, "dW": dW, "dba": dba}

        return gradients
        #整个网络的反向传播过程
def rnn_backward(ds, caches):
        """
        对给定的一个序列进行RNN的发现反向传播
        :param da:
        :param caches:
        :return:
        """

        # 获取第一个cell的数据,参数，输入输出值
        (s1, s0, x_1, parameters) = caches[0]

        # 获取总共cell的数量以及m和n的值
        n, _, T = ds.shape
        m, _ = x_1.shape

        # 初始化梯度值
        dx = np.zeros((m, 1, T))
        dU = np.zeros((n, m))
        dW = np.zeros((n, n))
        dba = np.zeros((n, 1))
        ds0 = np.zeros((n, 1))
        ds_prevt = np.zeros((n, 1))

        # 循环从后往前进行反向传播
        for t in reversed(range(T)):
            # 根据时间T的s梯度，以及缓存计算当前的cell的反向传播梯度.
            gradients = rnn_cell_backward(ds[:, :, t] + ds_prevt, caches[t])
            # 获取梯度准备进行更新
            dx_t, ds_prevt, dUt, dWt, dbat = gradients["dx_t"], gradients["ds_prev"], gradients["dU"], gradients[
                "dW"], gradients["dba"]
            # 进行每次t时间上的梯度接过相加，作为最终更新的梯度
            dx[:, :, t] = dx_t
            dU += dUt
            dW += dWt
            dba += dbat

        # 最后ds0的输出梯度值
        ds0 = ds_prevt
        # 存储需要更新的梯度到字典当中
        gradients = {"dx": dx, "ds0": ds0, "dU": dU, "dW": dW, "dba": dba}

        return gradients

---

总结

本周学习了RNN的正反向传播的过程，主要是了解RNN的时间反向传播算法。