机器学习中交叉熵cross entropy是什么，怎么计算？

项目背景：人体动作识别（分类），CNN或者RNN网络，softmax分类输出，输出为one-hot型标签。

---

loss可以理解为预测输出pred与实际输出Y之间的差距，其中pred和Y均为one-hot型。

计算loss的意义在于为接下来的optimizer提供优化的指标，即optimizer优化的目的为最小化loss。

在使用softmax层进行分类时，loss一般使用交叉熵cross_entropy：

cross_entropy = tf.nn.softmax_cross_entropy_with_logits_v2(labels=Y, logits=pred)
loss = tf.reduce_sum(cross_entropy)

假设每批训练数据量（batch_size)为N，那么cross_entropy的数量也为N，loss为将所有N个交叉熵相加的值。

其中涉及了两个函数：

---

（1）tf.nn.softmax_cross_entropy_with_logits_v2()

英文说明：

Computes softmax cross entropy between `logits` and `labels`.

即计算预测量与实际量的交叉熵（简单来说就是偏离值），另外它是适用于softmax输出的。

① 先看输入参数和返回值：

def softmax_cross_entropy_with_logits_v2(
    _sentinel=None,  # pylint: disable=invalid-name
    labels=None,
    logits=None,
    dim=-1,
    name=None):

# ···

    return cost

 其中labels为实际标签的概率比值，举例说明：

import numpy as np
import pandas as pd
labels = np.array(['Cat', 'Dog', 'Fish'])
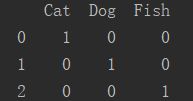
print(pd.get_dummies(labels))
labels_onehot = np.asarray(pd.get_dummies(labels))
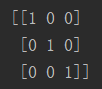
print(labels_onehot)

是指现在有三个input，标签labels分别是Cat、Dog和Fish:

我们可以对此这么理解：

input[0]的概率为Cat：100%， Dog：0%，Fish：0%

input[1]的概率为Cat：0%， Dog：100%，Fish：0%

input[2]的概率为Cat：0%， Dog：0%，Fish：100%

one-hot型式为：

这三个input在经过神经网络直到最后的softmax层后，会产生一组新的预测，即为logits：

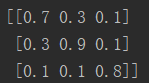
logits = np.array(([[0.7, 0.3, 0.1], [0.3, 0.9, 0.1], [0.1, 0.1, 0.8]]))

这组数据可以理解为：

input[0]的概率为Cat：70%， Dog：30%，Fish：10%

input[1]的概率为Cat：30%， Dog：90%，Fish：10%

input[2]的概率为Cat：10%， Dog：10%，Fish：80%

那么计算预测与实际之间的偏差，即可以得到cost返回值，也就是cross_entropy。

cross_entropy = tf.nn.softmax_cross_entropy_with_logits_v2(logits=logits, labels=labels_onehot)

with tf.Session() as sess:
    print(sess.run(cross_entropy))

这与我们的逻辑想法也是相符的，因为我们从上面可以看出对input[1]的预测是比input[0]的预测准确的，所以对input[1]的交叉熵计算也比input[0]小。

那么，这个函数是怎么计算交叉熵的呢？

② 直接上代码，自己写一个相同原理的函数softmax_cross_entropy(labels, logits)：

cross_entropy = tf.nn.softmax_cross_entropy_with_logits_v2(logits=logits, labels=labels_onehot)
loss = tf.reduce_sum(cross_entropy)

softmax_logits = tf.nn.softmax(logits)


def softmax_cross_entropy(labels, logits):
    cross_entropy_all = np.array([])
    for m in range(len(labels)):
        cross_entropy = 0
        for n in range(len(labels[0])):
            cross_entropy += math.log(logits[m][n]) * float(labels[m][n])
        cross_entropy_all = np.append(cross_entropy_all, -cross_entropy)
    return cross_entropy_all


with tf.Session() as sess:
    print("tf.nn.softmax_cross_entropy_with_logits_v2", sess.run(cross_entropy))
    # print("loss = ", sess.run(loss))
    real_softmax_logits = sess.run(softmax_logits)
    print("softmax_cross_entropy", softmax_cross_entropy(labels_onehot, real_softmax_logits))

用公式表达就是：

                            

* 需要注意的是softmax_cross_entropy_with_logits_v2会将输入自动用softmax函数计算一遍，

softmax = tf.exp(logits) / tf.reduce_sum(tf.exp(logits), axis)

这意味着在实际的应用中，如果你最后的输出层以及是softmax输出层（或者利用softmax做激励函数）

那么loss直接用以下方法计算即可等同于计算交叉熵。

loss = -tf.reduce_sum(Y * tf.log(tf.clip_by_value(pred, 1e-36, 1.0)))

---

（2）tf.reduce_sum()

英文说明：

Computes the sum of elements across dimensions of a tensor.

即计算一个多维tensor变量的相加值，举例说明：

For example:

```python
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x)  # 6
tf.reduce_sum(x, 0)  # [2, 2, 2]
tf.reduce_sum(x, 1)  # [3, 3]
tf.reduce_sum(x, 1, keepdims=True)  # [[3], [3]]
tf.reduce_sum(x, [0, 1])  # 6
```

cross_entropy = tf.nn.softmax_cross_entropy_with_logits_v2(logits=logits, labels=labels_onehot)
loss = tf.reduce_sum(cross_entropy)

with tf.Session() as sess:
    print(sess.run(cross_entropy))
    print("loss = ", sess.run(loss))

loss =  2.1790596743922306