神经网络与深度学习7---注意力机制与seq2seq模型

本文是邱锡鹏教授撰写的《神经网络与深度学习》一书中 第8章：注意力机制与外部记忆 的读书笔记，主要内容是一些本人觉得比较值得记录的内容，中间也会包括一些拓展和思考。

注意力评分函数

以下为注意力机制的流程图，查询 $\mathbf{q}$ 通过注意力评分函数 $a$ 与键 $\mathbf{k}$ 作用，并通过softmax得到对应 $\mathbf{k}$ 的概率分布值，最后这些概率分布值与值 $\mathbf{v}$ 做加权和：

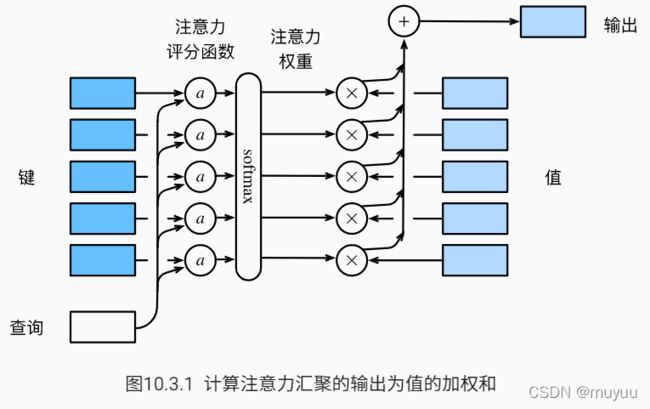
写成数学公式：
$$f(\mathbf{q},({\mathbf{k}}_1,{\mathbf{v}}_1),\cdots ,({\mathbf{k}}_m,{\mathbf{v}}_m))=\sum _{i=1}^m\text{softmax}(a(\mathbf{q},{\mathbf{k}}_i)){\mathbf{v}}_i=\sum _{i=1}^m\frac{\text{exp}(a(\mathbf{q},{\mathbf{k}}_i))}{{\sum }_{j=1}^m\text{exp}(a(\mathbf{q},{\mathbf{k}}_j))}{\mathbf{v}}_i$$

常用的注意力评分函数有 加性注意力 和 点积注意力 两种：

加性注意力：
$$a(\mathbf{q},\mathbf{k})={\mathbf{w}}_v^T\text{tanh}({\mathbf{W}}_q\cdot \mathbf{q}+{\mathbf{W}}_k\cdot \mathbf{k})\in \mathbb{R}$$
其中可学习参数 ${\mathbf{W}}_q\in {\mathbb{R}}^{h\times q},{\mathbf{W}}_k\in {\mathbb{R}}^{h\times k},{\mathbf{w}}_v\in {\mathbb{R}}^h$

点积注意力
$$a(\mathbf{q},{\mathbf{k}}_i)=\frac{{\mathbf{q}}^T{\mathbf{k}}_i}{\sqrt{d}}$$

点积评分函数计算效率更高，但是要求 $\mathbf{q}$ 和 $\mathbf{k}$ 具有相同的长度 $d$

在实践中，可以考虑批量计算注意力值来提升效率：
$$\text{softmax}(\frac{\mathbf{Q}{\mathbf{K}}^T}{\sqrt{d}})\mathbf{V}\in {\mathbb{R}}^{n\times v}$$

其中 $\mathbf{Q}\in {\mathbb{R}}^{n\times d}$ 表示 $n$ 个查询，$\mathbf{K}\in {\mathbb{R}}^{m\times d}$ 表示 $m$ 个键，$\mathbf{V}\in {\mathbb{R}}^{m\times v}$ 表示 $m$ 个值。

---

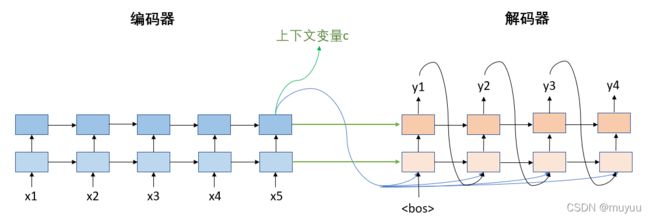
基于rnn的seq2seq模型

首先回忆基于循环神经网络的seq2seq模型：

如图所示：

1. encoder每一层最后时间步的state会作为decoder对应层state的初始化，因此要求encoder，decoder的层数一样，hidden_size 一样
2. 上下文变量 $\mathbf{c}$ 会与decoder上一时间步的输出 $y_{t-1}$ 拼接，作为当前时间步的输入

Note：在training时，decoder可以直接使用 y_gold 与 $\mathbf{c}$ 拼接作为输入；而在inference时，由于 y_gold 是不可知的，因此使用上一时间步的输出与$\mathbf{c}$ 拼接

这种结构的seq2seq会有一个问题：decoder所有时间步从encoder中获得的信息都是一样的，没有区分。但这与实际情况往往是不相符的，例如对于翻译模型，target language中的某个词往往会与source language的某一两个词具有强相关性，而跟其它的词相关性很弱。而注意力机制恰好就可以解决这样的问题。

---

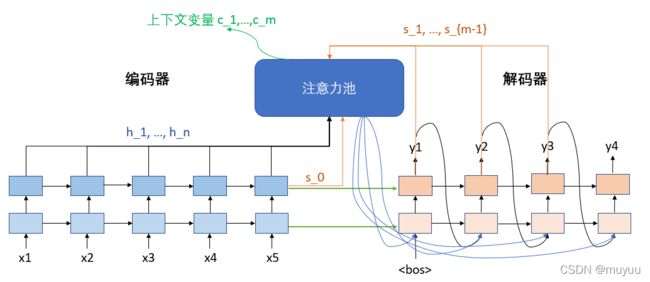
带注意力机制的基于rnn的seq2seq模型

带注意力机制的seq2seq模型中，上下文变量 $\mathbf{c}$ 不再简单的采用encoder的输出，而是encoder层隐变量与decoder上一时间步的注意力输出：
$${\mathbf{c}}_t=\sum _{i=1}^n\text{softmax}(a({\mathbf{s}}_{t-1},{\mathbf{h}}_i)){\mathbf{h}}_i$$

其中 ${\mathbf{s}}_{t-1}$ 是decoder上一时间步的隐层输出，${\mathbf{h}}_i$ 是encoder最后隐层的所有时间步的输出。

---

多头注意力

所谓“多头”，是通过给{查询，键，值}组合施加不同的线性变换来实现的，每个头的定义如下：

$$h_i=\sum _{t=1}^n\text{softmax}(a({\mathbf{W}}_i^q\mathbf{q},{\mathbf{W}}_i^k{\mathbf{k}}_t)){\mathbf{W}}_i^v{\mathbf{v}}_t\in {\mathbb{R}}^{p_v}$$

其中 ${\mathbf{W}}_i^q\in {\mathbb{R}}^{p_d\times d_q},{\mathbf{W}}_i^k\in {\mathbb{R}}^{p_k\times d_k},{\mathbf{W}}_i^v\in {\mathbb{R}}^{p_v\times d_v}$ 是可学习参数。

之后所有的头需要经过一个线性转换：
$${\mathbf{W}}^o\left[\begin{array}{c}{\mathbf{h}}_1\\ ⋮\\ {\mathbf{h}}_h\end{array}\right]\in {\mathbb{R}}^{p_o}$$

其中 ${\mathbf{W}}^o\in {\mathbb{R}}^{p_o\times h{p}_v}$ 也是可学习参数。

对同一 {查询，键，值} 施加不同的线性变换，并将这些结果组合起来，以此让模型学到比简单加权平均值更复杂的表示。

为了能够并行计算多个头，需要设置 $p_d=p_k=p_v=\frac{p_o}{h}$

---

Transfomer

论文地址：Attention Is All You Need

正如标题所表达的，Transfomer完全摒弃了循环神经网络的结构：

1. encoder层： {多头自注意力 + 前馈网络} $\times n$
2. decoder层： {掩蔽多头自注意力 + encoder-decoder多头自注意力 + 前馈网络} $\times n$

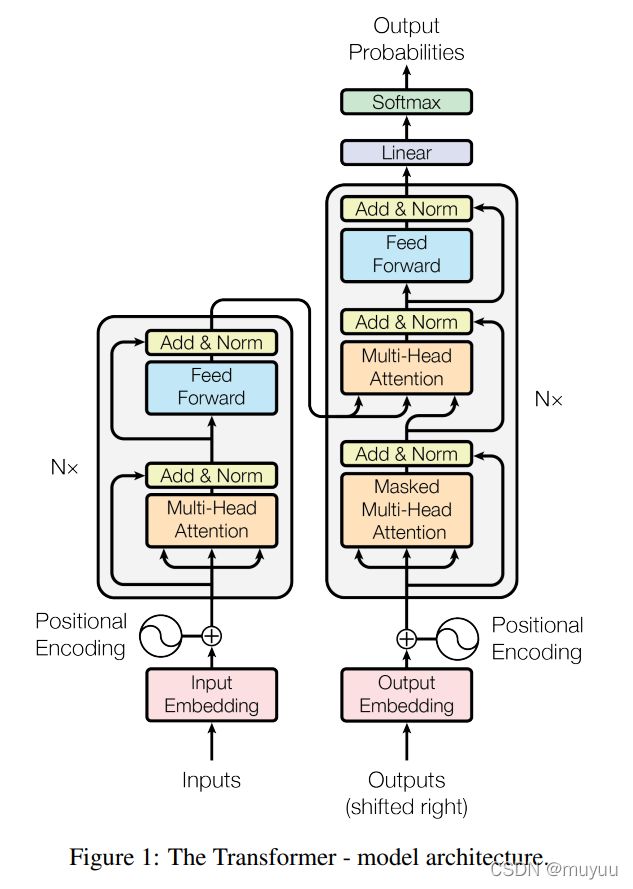
关于Transformer中注意力机制的详细使用情况，可以参加本人的另一篇博客 Transfomer矩阵维度分析及MultiHead详解

---

Reference:
动手学深度学习