机器学习笔记(2)——聚类之k-means算法
机器学习笔记(2)——聚类之Kmeans算法
一、k-means算法介绍
k-means算法是一种聚类算法,所谓聚类,即根据相似性原则,将具有较高相似度的数据对象划分至同一类簇,将具有较高相异度的数据对象划分至不同类簇。
聚类与分类最大的区别在于,聚类过程为无监督过程,即待处理数据对象没有任何先验知识,而分类过程为有监督过程,即存在有先验知识的训练数据集。
k-means算法是一种基于划分的聚类算法:算法以距离作为数据对象间相似性度量的标准,即数据对象间的距离越小,则它们的相似性越高,则它们越有可能在同一个类簇。数据对象间距离的计算有很多种,k-means算法通常采用欧氏距离来计算数据对象间的距离。
算法流程:
1.选择聚类的个数k.
2.任意产生k个聚类,然后确定聚类中心,或者直接生成k个中心。
3.对每个点确定其聚类中心点。
4.再计算其聚类新中心。
5.重复以上步骤直到满足收敛要求。(通常就是确定的中心点不再改变)
算法伪代码:
输入:训练数据集 D=x(1),x(2),...,x(m) ,聚类簇数 k ;
过程:函数 kMeans(D,k,maxIter) .
1:从 D 中随机选择 k 个样本作为初始“簇中心”向量: μ(1),μ(2),...,,μ(k) :
2:repeat
3: 令 Ci=∅(1≤i≤k)
4: for j=1,2,...,m do
5: 计算样本 x(j) 与各“簇中心”向量 μ(i)(1≤i≤k) 的欧式距离
6: 根据距离最近的“簇中心”向量确定 x(j) 的簇标记: λj=argmini∈{1,2,...,k}dji
7: 将样本 x(j) 划入相应的簇: Cλj=Cλj⋃{x(j)} ;
8: end for
9: for i=1,2,...,k do
10: 计算新“簇中心”向量: (μ(i))′=1|Ci|∑x∈Cix ;
11: if (μ(i))′=μ(i) then
12: 将当前“簇中心”向量 μ(i) 更新为 (μ(i))′
13: else
14: 保持当前均值向量不变
15: end if
16: end for
17: else
18:until 当前“簇中心”向量均未更新
输出:簇划分 C=C1,C2,...,CK二、算法特点
1、简单易实现,快速
2、对处理大数据集,该算法保持可伸缩性和高效率
3、当结果簇是密集的,它的效果较好
三、算法缺点
1、K值得选取不好确定
2、对于不是凸的数据集比较难收敛
3、如果各隐含类别的数据不平衡,比如各隐含类别的数据量严重失衡,或者各隐含类别的方差不同,则聚类效果较差
4、采用迭代方法,得到的结果只是局部最优。
5、对噪音和异常点比较的敏感
4、Python代码实现
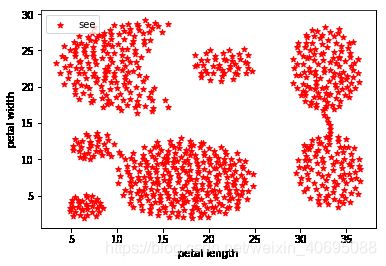
(1)使用Python内置函数,对数据集2Ddata.txt进行聚类
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
X = np.loadtxt('2Ddata.txt')
print(X)
#绘制数据分布图
plt.scatter(X[:, 0], X[:, 1], c = "red", marker='*', label='see')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()
estimator = KMeans(n_clusters=3)#构造聚类器
estimator.fit(X)#聚类
label_pred = estimator.labels_ #获取聚类标签
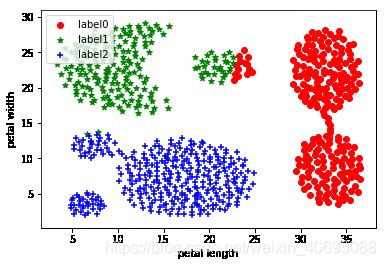
#绘制k-means结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
plt.scatter(x0[:, 0], x0[:, 1], c = "red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c = "green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c = "blue", marker='+', label='label2')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()数据集2Ddata.txt下载:https://pan.baidu.com/s/15r58ohVWUcywdXB2uEDv2w
(2)利用Python内置的鸢尾花数据集进行聚类
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
#from sklearn import datasets
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:]
print(X)
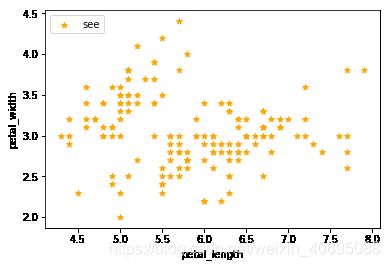
#'标签为sepal_len,sepal_width,petal_len,petal_width'花萼长度、花萼宽度、花瓣长度、花瓣宽度#绘制数据分布图
plt.scatter(X[:, 0], X[:, 1], c = "orange", marker='*', label='see')
plt.xlabel('petal_length')
plt.ylabel('petal_width')
plt.legend(loc=2)
plt.show()#聚类设定K=3
es = KMeans(n_clusters=3) #构造聚类器
es.fit(X) #聚类
label_pre = es.labels_ #获取聚类标签
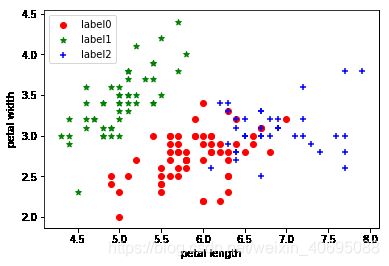
#绘制k-means结果
x0 = X[label_pre == 0]
x1 = X[label_pre == 1]
x2 = X[label_pre == 2]
plt.scatter(x0[:, 0], x0[:, 1], c = "red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c = "green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c = "blue", marker='+', label='label2')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()可以只选取特征空间中的后两个维度进行聚类
X = iris.data[:,2:] ###表示我们只取特征空间中的后两个维度