深度学习第二讲之卷积神经网络

鄙人的新书《elasticsearch7完全开发指南》，欢迎订阅！

https://wenku.baidu.com/view/8ff2ce94591b6bd97f192279168884868762b8e7

《kibana权威指南》

https://wenku.baidu.com/view/24cfee1ce43a580216fc700abb68a98270feac21

技术交流qq群： 659201069

视频教程：https://edu.csdn.net/course/detail/8587

转载请注明出处
本文引用了TensorFlow实战的部分内容，如果涉及版权问题，请您联系本人，本人将立即删除。[email protected]

机器学习的本质

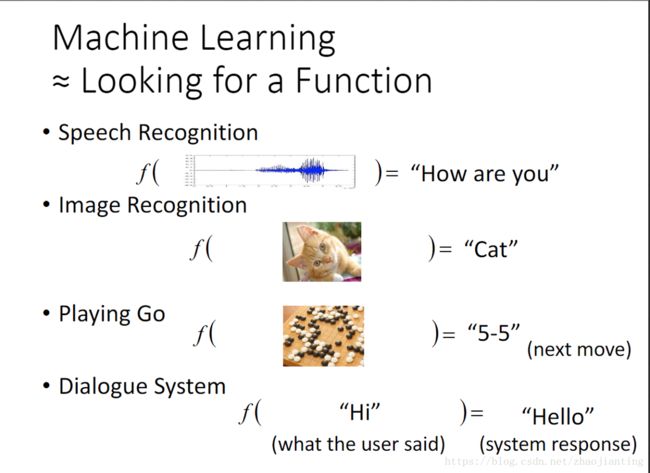
　　机器学习的本质，可以用上图来概括。深度学习是机器学习的一个分支，更准确得说是机器学习一种新的实现技术。机器学习就是寻找一个函数，这个函数可以根据输入给出输出即预测值，分类、回归、推荐等所有的机器学习都是为了找到一个函数。如何寻找这个函数据，一般情况下就是根据现有数据进行训练，函数更专业的述语是模型，训练得到的模型就是要找的函数。而深度学习的核心技术就是卷积运算。

卷积的数学定义

卷积运算源自于信号与系统学科，是指两个信号平移与叠加的过程。如下举例讲解，以离散信号为例，连续信号同理。
　　
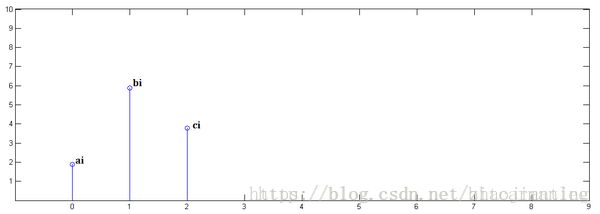
已知x[0] = a, x[1] = b, x[2]=c

已知y[0] = i, y[1] = j, y[2]=k

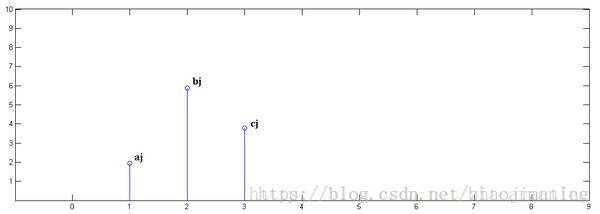
下面通过演示求x[n] * y[n]的过程，揭示卷积的物理意义。

第一步，x[n]乘以y[0]并平移到位置0：

第二步，x[n]乘以y[1]并平移到位置1

第三步，x[n]乘以y[2]并平移到位置2：

最后，把上面三个图叠加，就得到了x[n] * y[n]：

从这里，可以看到卷积的重要的物理意义是：一个函数（如：单位响应）在另一个函数（如：输入信号）上的加权叠加。

卷积在深度学习中的运用

以图片识别为例进行讲解。引用了http://setosa.io/ev/image-kernels/　的图片与内容

通过上图可以，可以从原始的图像矩阵，经过卷积运算，提取人的面部轮廓，其它这就是深度学习的核心从所，从基础的像素特征自动合成复杂的线条、轮廓等高层特征。深度学习主要的工作就是找一个卷积过滤矩阵（以下称过滤器），过滤器按照一定的步长在原始图像上移动，移动过程中与原始图像矩阵进行卷积运算，即点积运算，这经过点积运算，主要部位的特征像素加深（值是减小了，因为０是黑色），次要部位像素被忽略，反复多次，这样就可以提取出人的面部轮廓（其它图片的识别也是一样的原理，这里只是拿面部识别举例）。请看下图

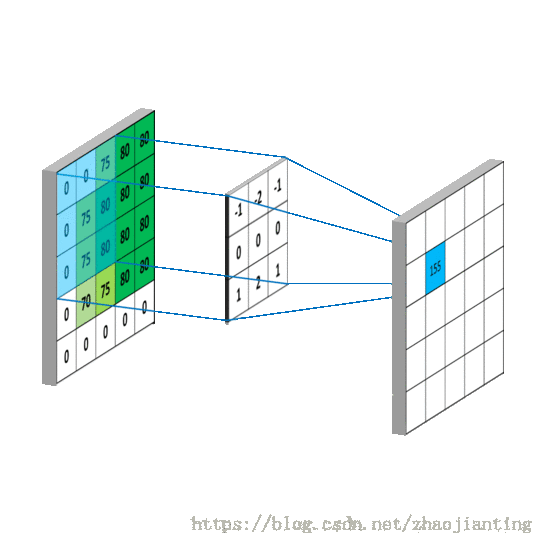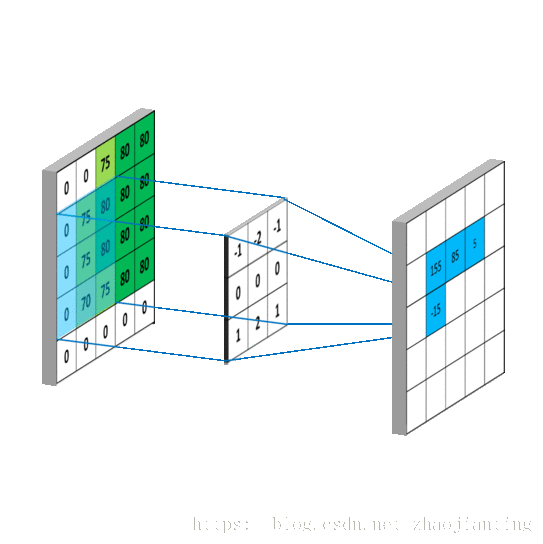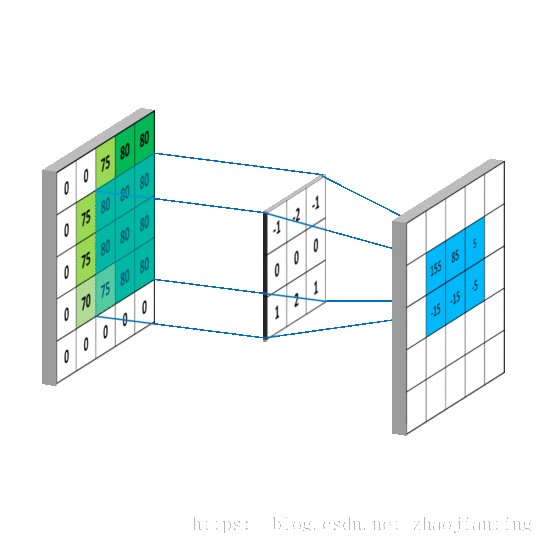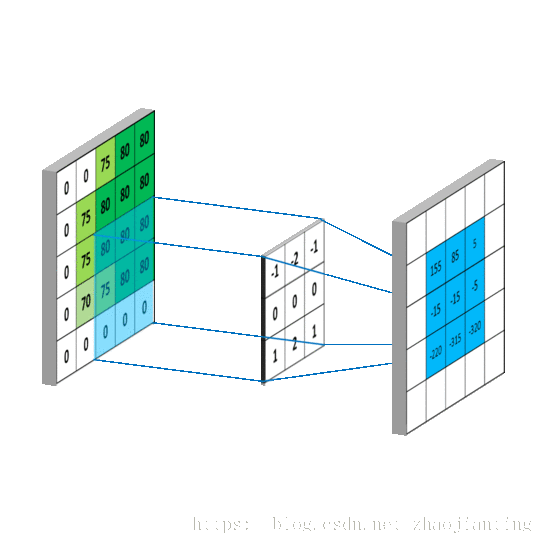
下图给出了使用了非全０真填充、步长为２的卷积层前向传播的计算结果

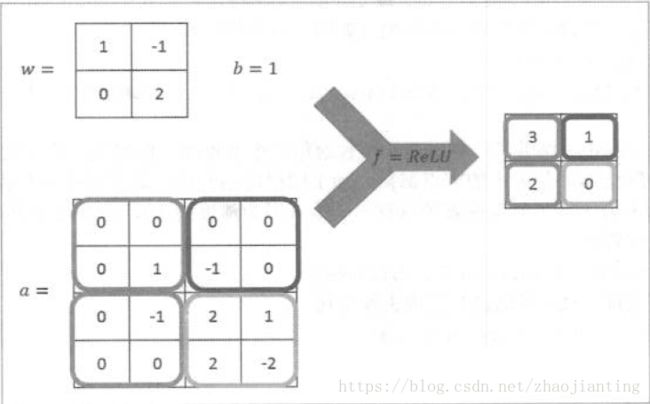
卷积层的计算过程就是通过将一个过滤器从神经网络当前层的左上角移动到右下角，并且在移动过程中计算每一个对应的单位矩阵（即过滤器矩阵与其对应区域的点积）。

卷积神经网络结构

典型的卷积神经网络模型如下图所示

LeNet-5模型

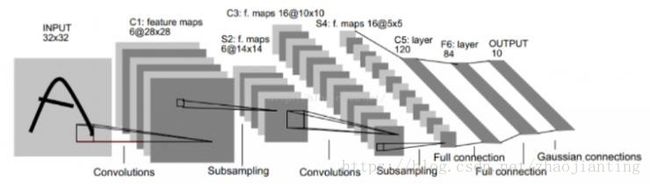
LeNet-5模型定义了CNN的基本组件，是CNN的鼻祖。
　　LeNet是卷积神经网络的祖师爷LeCun在1998年提出，用于解决手写数字识别的视觉任务。自那时起，CNN的最基本的架构就定下来了：卷积层、池化层、全连接层。如今各大深度学习框架中所使用的LeNet都是简化改进过的LeNet-5（-5表示具有5个层），和原始的LeNet有些许不同，比如把激活函数改为了现在很常用的ReLu。
　　LeNet-5跟现有的conv->pool->ReLU的套路不同，它使用的方式是conv1->pool->conv2->pool2再接全连接层，但是不变的是，卷积层后紧接池化层的模式依旧不变。

对经典的LeNet-5做深入分析：
首先输入图像是单通道的2828大小的图像，用矩阵表示就是[1,28,28]
第一个卷积层conv1所用的卷积核尺寸为55，滑动步长为1，卷积核数目为20，那么经过该层后图像尺寸变为24，28-5+1=24，输出矩阵为[20,24,24]。
第一个池化层pool核尺寸为22，步长2，这是没有重叠的max pooling，池化操作后，图像尺寸减半，变为12×12，输出矩阵为[20,12,12]。
第二个卷积层conv2的卷积核尺寸为55，步长1，卷积核数目为50，卷积后图像尺寸变为8,这是因为12-5+1=8，输出矩阵为[50,8,8].
第二个池化层pool2核尺寸为2*2，步长2，这是没有重叠的max pooling，池化操作后，图像尺寸减半，变为4×4，输出矩阵为[50,4,4]。
pool2后面接全连接层fc1，神经元数目为500，再接relu激活函数。
再接fc2，神经元个数为10，得到10维的特征向量，用于10个数字的分类训练，送入softmaxt分类，得到分类结果的概率output。

通用逼近定理(Universal Approximation Theorem)
　　这个定理要说明的是神经网络可以拟合一切函数
　　一个仅有单隐藏层的神经网络。在神经元个数足够多的情况下，通过非线性的激活函数，足以拟合任意函数。这使得我们在思考神经网络的问题的时候，不需要考虑：我的函数是否能够用神经网络拟合，因为他永远可以做到——只需要考虑如何用神经网络做到更好的拟合。
　　更多资料可以参考***http://neuralnetworksanddeeplearning.com/chap4.html***

下面通过一个图别识别的具体应用来讲解Le-Net-5模型中各层所需完成的功能

　　图片识别领域需要解决的问题是，在一定数量的图片数据上训练得到一个模型，通过这个模型可以对输入的图片进行正确的分类。2012年多伦多大学的Krizhevsky等人构造了一个超大型卷积神经网络[1]，有9层，共65万个神经元，6千万个参数,网络的输入是图片，输出是1000个类，比如小虫、美洲豹、救生船等等。这个模型的训练需要海量图片，，它的分类准确率也完爆先前所有分类器。纽约大学的Zeiler和Fergusi[2]把这个网络中某些神经元挑出来，把在其上响应特别大的那些输入图像放在一起，看它们有什么共同点。他们发现中间层的神经元响应了某些十分抽象的特征。

第一层神经元主要负责识别颜色和简单纹理

**第二层的一些神经元可以识别更加细化的纹理，比如布纹、刻度、叶纹。


第三层的一些神经元负责感受黑夜里的黄色烛光、鸡蛋黄、高光。


第四层的一些神经元负责识别萌狗的脸、七星瓢虫和一堆圆形物体的存在。

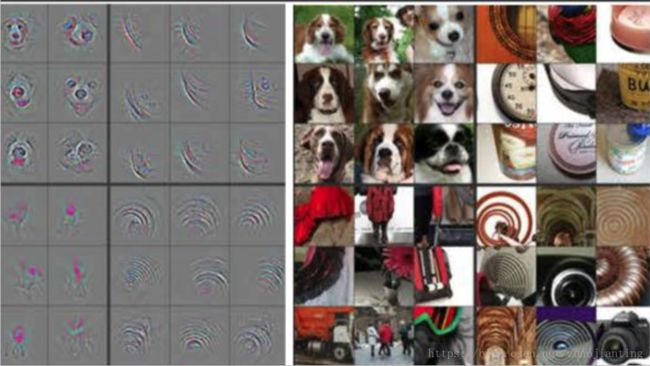
第五层的一些神经元可以识别出花、圆形屋顶、键盘、鸟、黑眼圈动物。

结构发展

• 以下是几个比较有名的卷积神经网络结构，。
• LeNet：第一个成功的卷积神经网络应用
• AlexNet:类似LeNet，但更深更大。使用了层叠的卷积层来抓取特征（通常是一个卷积层马上一个max pooling层)
• VGGNet：只使用3x3 卷积层和2x2 pooling层从头到尾堆叠。 ResNet：引入了跨层连接和batch　normalization

LeNet模型上面已作了详细分析，下面解介绍AlexNet和VGGNet模型

王者归来：AlexNet

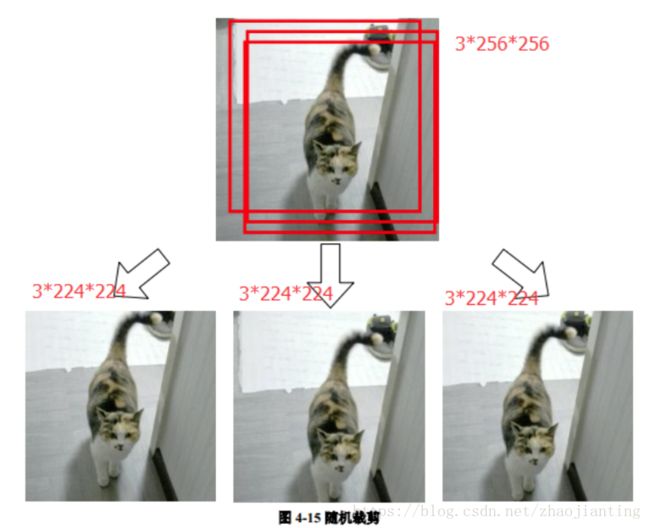
• 数据增广技巧来增加模型泛化能力。
• 用ReLU代替Sigmoid来加快SGD的收敛速度
• Dropout有效缓解了模型的过拟合。

Dropout:Dropout原理类似于浅层学习算法的中集成算法，该方法通过让全连接层的神经元（该模型在前两个全连接层引入Dropout）以一定的概率失去活性（比如0.5）失活的神经元不再参与前向和反向传播，相当于约有一半的神经元不再起作用。在测试的时候，让所有神经元的输出乘0.5。Dropout的引用，有效缓解了模型的过拟合。

越走越深：VGG-Nets

• 卷积层使用更小的filter尺寸和间隔
• 3×3卷积核的优点：多个3×3的卷基层比一个大尺寸filter卷基层有更多的非线性，使得判决函数更加具有判决性
• 1*1卷积核的优点：作用是在不影响输入输出维数的情况下，对输入进行线性形变，然后通过Relu进行非线性处理，增加网络的非线性表达能力

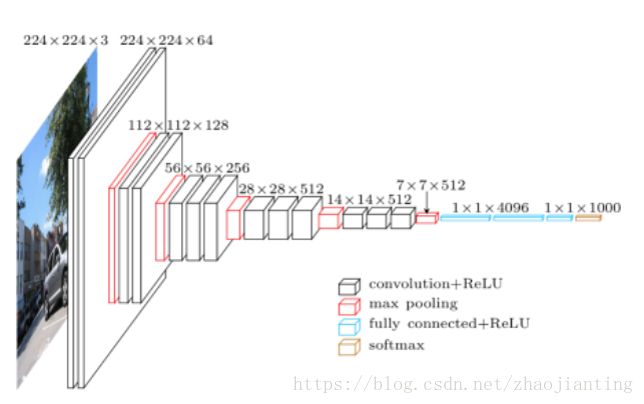
由上图看出，VGG-16的结构非常整洁，深度较AlexNet深得多，里面包含多个conv->conv->max_pool这类的结构,VGG的卷积层都是same的卷积，即卷积过后的输出图像的尺寸与输入是一致的，它的下采样完全是由max pooling来实现。
VGG网络后接3个全连接层，filter的个数（卷积后的输出通道数）从64开始，然后没接一个pooling后其成倍的增加，128、512，VGG的注意贡献是使用小尺寸的filter，及有规则的卷积-池化操作。
　　闪光点：
卷积层使用更小的filter尺寸和间隔
与AlexNet相比，可以看出VGG-Nets的卷积核尺寸还是很小的，比如AlexNet第一层的卷积层用到的卷积核尺寸就是1111，这是一个很大卷积核了。而反观VGG-Nets，用到的卷积核的尺寸无非都是1×1和3×3的小卷积核，可以替代大的filter尺寸。
3×3卷积核的优点：
多个3×3的卷基层比一个大尺寸filter卷基层有更多的非线性，使得判决函数更加具有判决性
多个3×3的卷积层比一个大尺寸的filter有更少的参数，假设卷基层的输入和输出的特征图大小相同为C，那么三个3×3的卷积层参数个数3×（3×3×C×C）=27CC；一个7×7的卷积层参数为49CC；所以可以把三个3×3的filter看成是一个7×7filter的分解（中间层有非线性的分解）
11卷积核的优点：
作用是在不影响输入输出维数的情况下，对输入进行线性形变，然后通过Relu进行非线性处理，增加网络的非线性表达能力。

里程碑式创新：ResNet

• 2015年何恺明推出的ResNet在ISLVRC和COCO上横扫所有选手，获得冠军
• 层数非常深，已经超过百层
• 引入残差单元来解决退化问题

2015年何恺明推出的ResNet在ISLVRC和COCO上横扫所有选手，获得冠军。ResNet在网络结构上做了大创新，而不再是简单的堆积层数，ResNet在卷积神经网络的新思路，绝对是深度学习发展历程上里程碑式的事件。

闪光点：
层数非常深，已经超过百层
引入残差单元来解决退化问题
　　从前面可以看到，随着网络深度增加，网络的准确度应该同步增加，当然要注意过拟合问题。但是网络深度增加的一个问题在于这些增加的层是参数更新的信号，因为梯度是从后向前传播的，增加网络深度后，比较靠前的层梯度会很小。这意味着这些层基本上学习停滞了，这就是梯度消失问题。深度网络的第二个问题在于训练，当网络更深时意味着参数空间更大，优化问题变得更难，因此简单地去增加网络深度反而出现更高的训练误差，深层网络虽然收敛了，但网络却开始退化了，即增加网络层数却导致更大的误差，比如下图，一个56层的网络的性能却不如20层的性能好，这不是因为过拟合（训练集训练误差依然很高），这就是烦人的退化问题。残差网络ResNet设计一种残差模块让我们可以训练更深的网络。

这里详细分析一下残差单元来理解ResNet的精髓。
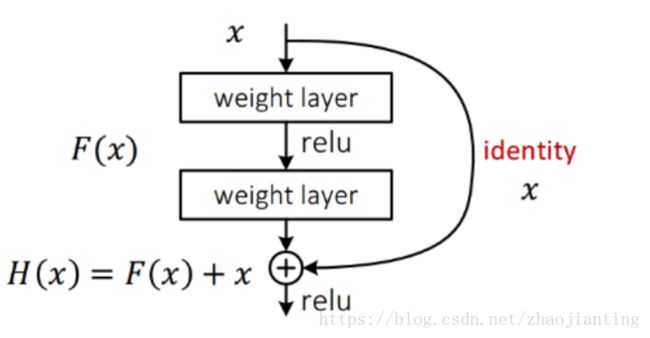
　　从下图可以看出，数据经过了两条路线，一条是常规路线，另一条则是捷径（shortcut），直接实现单位映射的直接连接的路线，这有点类似与电路中的“短路”。通过实验，这种带有shortcut的结构确实可以很好地应对退化问题。我们把网络中的一个模块的输入和输出关系看作是y=H(x)，那么直接通过梯度方法求H(x)就会遇到上面提到的退化问题，如果使用了这种带shortcut的结构，那么可变参数部分的优化目标就不再是H(x),若用F(x)来代表需要优化的部分的话，则H(x)=F(x)+x，也就是F(x)=H(x)-x。因为在单位映射的假设中y=x就相当于观测值，所以F(x)就对应着残差，因而叫残差网络。为啥要这样做，因为作者认为学习残差F(X)比直接学习H(X)简单！设想下，现在根据我们只需要去学习输入和输出的差值就可以了，绝对量变为相对量（H（x）-x 就是输出相对于输入变化了多少），优化起来简单很多。
　　考虑到x的维度与F(X)维度可能不匹配情况，需进行维度匹配。这里论文中采用两种方法解决这一问题(其实是三种，但通过实验发现第三种方法会使performance急剧下降，故不采用):
　　zero_padding:对恒等层进行0填充的方式将维度补充完整。这种方法不会增加额外的参数
　　projection:在恒等层采用1x1的卷积核来增加维度。这种方法会增加额外的参数

上面两张展示了两种形态的残差模块，第一张图是常规残差模块，有两个3×3卷积核卷积核组成，但是随着网络进一步加深，这种残差结构在实践中并不是十分有效。针对这问题，第二张图的“瓶颈残差模块”（bottleneck residual block）可以有更好的效果，它依次由1×1、3×3、1×1这三个卷积层堆积而成，这里的1×1的卷积能够起降维或升维的作用，从而令3×3的卷积可以在相对较低维度的输入上进行，以达到提高计算效率的目的。