金融风控(贷款违约预测)
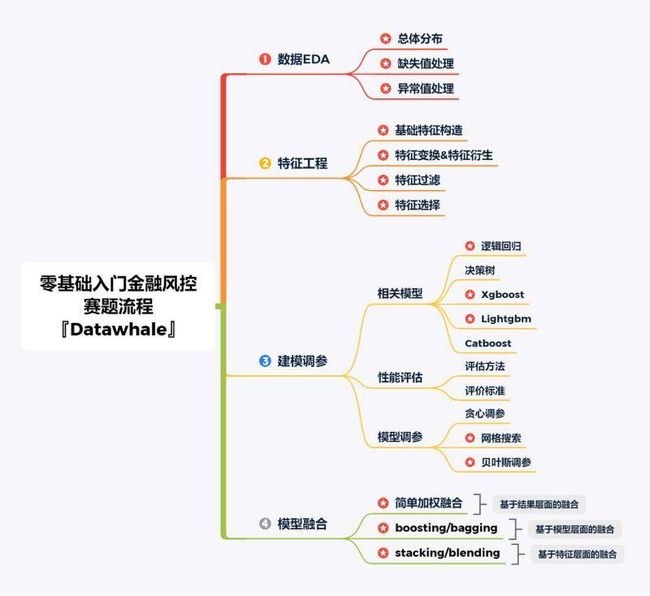
Task1赛题理解
Tip:本次新人赛是Datawhale与天池联合发起的0基础入门系列赛事第四场 —— 零基础入门金融风控之贷款违约预测挑战赛。 赛题以金融风控中的个人信贷为背景,要求选手根据贷款申请人的数据信息预测其是否有违约的可能,以此判断是否通过此项贷款,这是一个典型的分类问题。通过这道赛题来引导大家了解金融风控中的一些业务背景,解决实际问题,帮助竞赛新人进行自我练习、自我提高。
项目地址:
https://github.com/datawhalechina/team-learning-data-mining/tree/master/FinancialRiskControl
比赛地址:
https://tianchi.aliyun.com/competition/entrance/531830/introduction
1.1 学习目标
理解赛题数据和目标,清楚评分体系。
完成相应报名,下载数据和结果提交打卡(可提交示例结果),熟悉比赛流程
1.2 了解赛题
- 赛题概况
- 数据概况
- 预测指标
- 分析赛题
1.2.1 赛题概况
比赛要求参赛选手根据给定的数据集,建立模型,预测金融风险。
赛题以预测金融风险为任务,数据集报名后可见并可下载,该数据来自某信贷平台的贷款记录,总数据量超过120w,包含47列变量信息,其中15列为匿名变量。为了保证比赛的公平性,将会从中抽取80万条作为训练集,20万条作为测试集A,20万条作为测试集B,同时会对employmentTitle、purpose、postCode和title等信息进行脱敏。
通过这道赛题来引导大家走进金融风控数据竞赛的世界,主要针对于于竞赛新人进行自我练习、自我提高。
1.2.2 数据概况
一般而言,对于数据在比赛界面都有对应的数据概况介绍(匿名特征除外),说明列的性质特征。了解列的性质会有助于我们对于数据的理解和后续分析。 Tip:匿名特征,就是未告知数据列所属的性质的特征列。
- id 为贷款清单分配的唯一信用证标识
- loanAmnt 贷款金额
- term 贷款期限(year)
- interestRate 贷款利率
- installment 分期付款金额
- grade 贷款等级
- subGrade 贷款等级之子级
- employmentTitle 就业职称
- employmentLength 就业年限(年)
- homeOwnership 借款人在登记时提供的房屋所有权状况
- annualIncome 年收入
- verificationStatus 验证状态
- issueDate 贷款发放的月份
- purpose 借款人在贷款申请时的贷款用途类别
- postCode 借款人在贷款申请中提供的邮政编码的前3位数字
- regionCode 地区编码
- dti 债务收入比
- delinquency_2years 借款人过去2年信用档案中逾期30天以上的违约事件数
- ficoRangeLow 借款人在贷款发放时的fico所属的下限范围
- ficoRangeHigh 借款人在贷款发放时的fico所属的上限范围
- openAcc 借款人信用档案中未结信用额度的数量
- pubRec 贬损公共记录的数量
- pubRecBankruptcies 公开记录清除的数量
- revolBal 信贷周转余额合计
- revolUtil 循环额度利用率,或借款人使用的相对于所有可用循环信贷的信贷金额
- totalAcc 借款人信用档案中当前的信用额度总数
- initialListStatus 贷款的初始列表状态
- applicationType 表明贷款是个人申请还是与两个共同借款人的联合申请
- earliesCreditLine 借款人最早报告的信用额度开立的月份
- title 借款人提供的贷款名称
- policyCode 公开可用的策略_代码=1新产品不公开可用的策略_代码=2
- n系列匿名特征 匿名特征n0-n14,为一些贷款人行为计数特征的处理
1.2.3 预测指标
竞赛采用AUC作为评价指标。AUC(Area Under Curve)被定义为 ROC曲线 下与坐标轴围成的面积。
分类算法常见的评估指标如下:
1、混淆矩阵(Confuse Matrix)
- (1)若一个实例是正类,并且被预测为正类,即为真正类TP(True Positive )
- (2)若一个实例是正类,但是被预测为负类,即为假负类FN(False Negative )
- (3)若一个实例是负类,但是被预测为正类,即为假正类FP(False Positive )
- (4)若一个实例是负类,并且被预测为负类,即为真负类TN(True Negative )
2、准确率(Accuracy) 准确率是常用的一个评价指标,但是不适合样本不均衡的情况。 A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy = \frac{TP + TN}{TP + TN + FP + FN} Accuracy=TP+TN+FP+FNTP+TN
3、精确率(Precision) 又称查准率,正确预测为正样本(TP)占预测为正样本(TP+FP)的百分比。 P r e c i s i o n = T P T P + F P Precision = \frac{TP}{TP + FP} Precision=TP+FPTP
4、召回率(Recall) 又称为查全率,正确预测为正样本(TP)占正样本(TP+FN)的百分比。 R e c a l l = T P T P + F N Recall = \frac{TP}{TP + FN} Recall=TP+FNTP
5、F1 Score 精确率和召回率是相互影响的,精确率升高则召回率下降,召回率升高则精确率下降,如果需要兼顾二者,就需要精确率、召回率的结合F1 Score。 F 1 − S c o r e = 2 1 P r e c i s i o n + 1 R e c a l l F1-Score = \frac{2}{\frac{1}{Precision} + \frac{1}{Recall}} F1−Score=Precision1+Recall12
6、P-R曲线(Precision-Recall Curve) P-R曲线是描述精确率和召回率变化的曲线
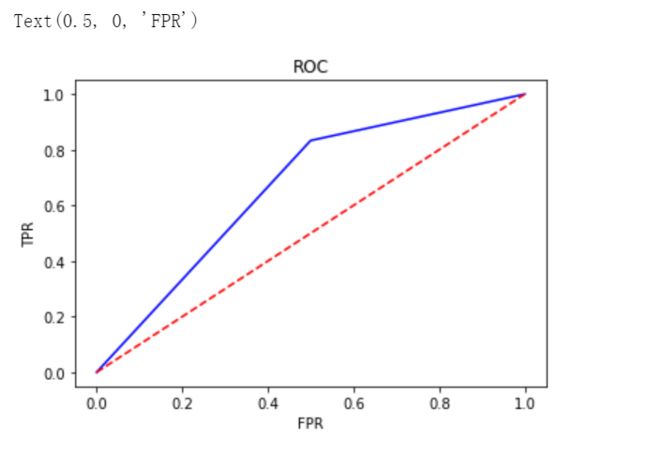
7、ROC(Receiver Operating Characteristic)
- ROC空间将假正例率(FPR)定义为 X 轴,真正例率(TPR)定义为 Y 轴。
TPR:在所有实际为正例的样本中,被正确地判断为正例之比率。
T P R = T P T P + F N TPR = \frac{TP}{TP + FN} TPR=TP+FNTP
FPR:在所有实际为负例的样本中,被错误地判断为正例之比率。
F P R = F P F P + T N FPR = \frac{FP}{FP + TN} FPR=FP+TNFP

8、AUC(Area Under Curve) AUC(Area Under Curve)被定义为 ROC曲线 下与坐标轴围成的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。AUC越接近1.0,检测方法真实性越高;等于0.5时,则真实性最低,无应用价值。
对于金融风控预测类常见的评估指标如下:
1、KS(Kolmogorov-Smirnov) KS统计量由两位苏联数学家A.N. Kolmogorov和N.V. Smirnov提出。在风控中,KS常用于评估模型区分度。区分度越大,说明模型的风险排序能力(ranking ability)越强。 K-S曲线与ROC曲线类似,不同在于
- ROC曲线将真正例率和假正例率作为横纵轴
- K-S曲线将真正例率和假正例率都作为纵轴,横轴则由选定的阈值来充当。 公式如下: K S = m a x ( T P R − F P R ) KS=max(TPR-FPR) KS=max(TPR−FPR) KS不同代表的不同情况,一般情况KS值越大,模型的区分能力越强,但是也不是越大模型效果就越好,如果KS过大,模型可能存在异常,所以当KS值过高可能需要检查模型是否过拟合。以下为KS值对应的模型情况,但此对应不是唯一的,只代表大致趋势。
| KS(%) | 好坏区分能力 |
|---|---|
| 20以下 | 不建议采用 |
| 20-40 | 较好 |
| 41-50 | 良好 |
| 51-60 | 很强 |
| 61-75 | 非常强 |
| 75以上 | 过于高,疑似存在问题 |
2、ROC
3、AUC
本部分为对于数据读取和指标评价的示例。
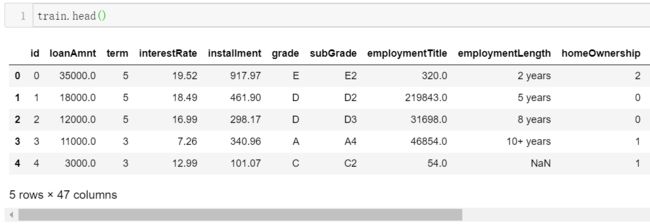
1.3.1 数据读取pandas
import pandas as pd
train = pd.read_csv('train.csv')
testA = pd.read_csv('testA.csv')
print('Train data shape:',train.shape)
print('TestA data shape:',testA.shape)Train data shape: (800000,47)
TestA data shape:(200000,48)
(1)混淆矩阵
##混淆矩阵
import numpy as np
from sklearn.metrics import confusion_matrix
y_pred = [0,1,0,1]
y_true = [0,1,1,0]
print('混淆矩阵:\n',confusion_matrix(y_true,y_pred))混淆矩阵:
[[1 1]
[1 1]]
(2)accuracy
##accuracy
from sklearn.metrics import accuracy_score
y_pred = [0,1,0,1]
y_true = [0,1,1,0]
print('ACC:\',accuracy_score(y_true,y_pred))ACC: 0.5
(3)Precision,Recall,F1-score
##Precision,Recall,F1-score
from sklearn import metrics
y_pred = [0,1,0,1]
y_true = [0,1,1,0]
print('Precision',metrics.precision_score(y_true,y_pred))
print('Recall',metrics.recall_score(y_true,y_pred))
print('F1-score:',metrics.f1-score(y_true,y_pred))Precision 0.5
Recall 0.5
F1-score 0.5
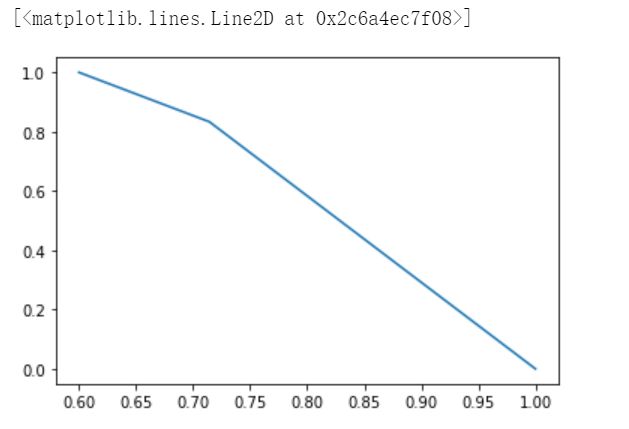
(4)P-R 曲线
## P-R曲线
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
y_pred = [0,1,1,0,1,1,0,1,1,1]
y_true = [0,1,1,0,1,0,1,1,0,1]
precision,recall,thresholds = precision_recall_curve(y_true,y_pred)
plt.plot(precision,recall)## ROC曲线
from sklearn.metrics import roc_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
FPR,TPR,thresholds=roc_curve(y_true, y_pred)
plt.title('ROC')
plt.plot(FPR, TPR,'b')
plt.plot([0,1],[0,1],'r--')
plt.ylabel('TPR')
plt.xlabel('FPR')## AUC
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
print('AUC socre:',roc_auc_score(y_true, y_scores))AUC socre: 0.75
(7)KS值
## KS值 在实际操作时往往使用ROC曲线配合求出KS值
from sklearn.metrics import roc_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 1, 1]
FPR,TPR,thresholds=roc_curve(y_true, y_pred)
KS=abs(FPR-TPR).max()
print('KS值:',KS)KS值: 0.5238095238095237
1.4 经验总结
赛题理解是开始比赛的第一步,赛题的理解有助于对竞赛全局的把握。通过赛题理解有助于对赛题的业务逻辑把握,对于后期的特征工程构建和模型选择都尤为重要。
-
在开始比赛之前要对赛题进行充分的了解。
-
比赛什么时候开始,什么时候结束,什么时候换B榜数据。
-
和该比赛有没有类似的比赛可以参考借鉴。
-
线上提交结果的次数往往是有限的,提前了解每日可以提交的次数。
-
比赛使用的是什么评价指标,可以选择相同的评价指标作为线下验证的方式。
1.5 拓展知识——评分卡
评分卡是一张拥有分数刻度会让相应阈值的表。信用评分卡是用于用户信用的一张刻度表。以下代码是一个非标准评分卡的代码流程,用于刻画用户的信用评分。评分卡是金融风控中常用的一种对于用户信用进行刻画的手段!
#评分卡 不是标准评分卡
def Score(prob,P0=600,PDO=20,badrate=None,goodrate=None):
P0 = P0
PDO = PDO
theta0 = badrate/goodrate
B = PDO/np.log(2)
A = P0 + B*np.log(2*theta0)
score = A-B*np.log(prob/(1-prob))
return scoreEND. 【GRQ :Datawhale参与者,金融风控爱好者。】