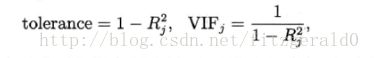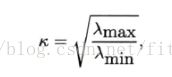矩阵存在共线性的第二谈

前面一篇文章中我们谈了非正定的问题。那么，针对Mplus中的这个警告做一点解释

THE MODEL ESTIMATION TERMINATED NORMALLY

     THE STANDARD ERRORS OF THE MODEL PARAMETER ESTIMATES MAY NOT BE

     TRUSTWORTHY FOR SOME PARAMETERS DUE TO A NON-POSITIVE DEFINITE

     FIRST-ORDER DERIVATIVE PRODUCT MATRIX.  THIS MAY BE DUE TO THE STARTING

     VALUES BUT MAY ALSO BE AN INDICATION OF MODEL NONIDENTIFICATION.  THE

     CONDITION NUMBER IS      -0.378D-16.  PROBLEM INVOLVING THE FOLLOWING PARAMETER；

先来看这个数据集，一个著名的共线性数据集，具体内容见这个链接

http://www.itl.nist.gov/div898/strd/lls/data/Longley.shtml

先把上面出现的那个提示解释一下，

关于这个问题，很多人提问Mplus作者貌似压根没有说明白

http://www.statmodel.com/discussion/messages/11/1602.html?1475195929

矩阵的条件数（condition number）

condition number 是一个矩阵的稳定性或者敏感度的度量，如果一个矩阵的 condition number在1附近，那么它就是well-conditioned的，如果远离1，它的输出结果就不可相信。本数据的矩阵条件数是-0.378D-16，这是科学计数法，网上没有查到具体是多少。

关于共线性的度量主要有三个：

1 容忍度（tolerance), 

2 方差膨胀因子（variable inflation factor,VIF）

3条件数，常用k表示

r容忍度和 VIF的定义

一般vif太大比如大于10，则说明存在多重共线性

条件数K

在计算函数值f(x)时，如果有x扰动,x相对误差为

函数值的相对误差为，

则相对误差比值为：

称为计算函数值问题的条件数，当条件数大于等于10，认为是病态

或者在矩阵中，矩阵特征值最大比上最小，当自变量正交时，条件数为1，当k>15时存在共线性问题

 在矩阵运算中，常常需要考虑观察数据存在某种程度的不确定性和误差，而且在数据计算也总是伴随着误差，同时我们还需要关注在牛顿迭代过程中算法的稳定性，给定方程求解其中的某个解集 d，我们希望得到的近似值d* 如果f(d)逼近f(d*)那么这个算法在求解此问题是就是“良性”的，如果在逼近f(d*)有时相差很大，那么我们就称为“病态”。我们只有在保证算法稳定的前提下让f(d)逼近f(d*)计算出的结果才是可信的。

 在求解线性方程AX=b时，其中矩阵A是 n*n的元素为已知数值的系数矩阵，b是n*1的已知向量，X是一个待求解的参数向量，系数矩阵A非奇异时，由于独立方程的个数和未知参数的个数相等，故方程有唯一的解，成为正定方程，这时我们对求解的稳定性感兴趣，如果系数矩阵A和向量矩阵b发生扰动，那么方程的解向量X如何变化，如果解向量X如何受系数矩阵A和系数向量b的元素微小扰动的影响，将得到描述矩阵A的一个重要特征数值称为条件数(condition number)，在 matlab中

函数是cond同时在python求解用np.linalg.cond() 这个指令。关于cond的计算在间文末的附录

 当系数矩阵A一个很小的扰动引起向量X很小的扰动，则称A为(well-condition matrix)良态矩阵，若引起很大的扰动，则称矩阵A是(ill-condition matrix)病态，而条件数则是衡量求解线性方程，误差的通过矩阵A的传播扩大为解向量的误差程度，也就是说，是衡量线性方程数值稳定性的一个重要指标。

我们再来看看

Mplus语句和本数据输出的结果

    data: file is longnm.csv;

    variable: names are y x1-x6;

    model:x1-x6 on y;

    output:modindices tech1 tech4;

tech4出现这样的相关矩阵

           ESTIMATED CORRELATION MATRIX FOR THE LATENT VARIABLES

              X1            X2            X3            X4            X5

              ________      ________      ________      ________      ________

 X1             1.000

 X2             0.992         1.000

 X3             0.621         0.604         1.000

 X4             0.465         0.446        -0.177         1.000

 X5             0.979         0.991         0.687         0.364         1.000

 X6             0.991         0.995         0.668         0.417         0.994

 Y              0.971         0.984         0.502         0.457         0.960

想必也看到了，这个矩阵的存在大量相关系数大于0.9的变量

那么提示是存在着共线性了。