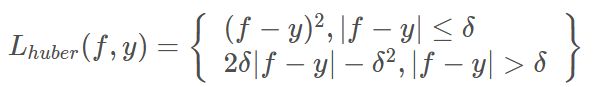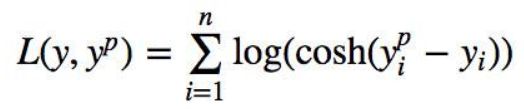Pytorch学习--回归损失函数总结
“损失函数”是机器学习优化中至关重要的一部分。机器学习中所有的算法都需要最大化或最小化一个函数,这个函数被称为“目标函数”。其中,我们一般把最小化的一类函数,称为“损失函数”。它能根据预测结果,衡量出模型预测能力的好坏。常见的损失函数例如L1、L2损失函数。除此之外,还有Huber损失、Log-Cosh损失、以及常用于计算预测区间的分位数损失。
在实际应用中,选取损失函数会受到诸多因素的制约,比如是否有异常值、机器学习算法的选择、梯度下降的时间复杂度、求导的难易程度以及预测值的置信度等等。因此,不存在一种损失函数适用于处理所有类型的数据。
损失函数大致可分为两类:分类问题的损失函数和回归问题的损失函数。在此将着重介绍回归损失。
损失函数的定义
损失函数就是用来衡量模型预测的好坏,表现预测与实际数据的差距程度 。估量模型的预测值f(x)与真实值Y的不一致程度,它是一个非负实值函数。通常使用L(Y, f(x))来表示,损失函数越小,模型的鲁棒性就越好。
损失函数,又叫目标函数,刻画了模型与训练样本的匹配程度,是编译一个神经网络模型必须的两个要素之一。另一个必不可少的要素是优化器。用来评价模型的预测值和真实值不一样的程度 ,损失函数越好,通常模型的性能越好,不同的模型用的损失函数一般也不一样。
损失函数分为经验风险损失函数和结构风险损失函数 。经验风险损失函数指预测结果和实际结果的差别,结构风险损失函数是指经验风险损失函数加上正则项 。损失Loss必须是标量 ,因为向量无法比较大小(向量本身需要通过范数等标量来比较)。
为何要设定损失函数
神经网络中的“ 学习 ”是指从训练数据中 自动 获取最优权重参数的过程。学习的目的就是以该损失函数为基准,找出能使它的值达到最小的权重参数。
1.对于回归问题,期望 f(xi,θ)≈yi
(1)Square损失:![]()
平方损失函数是光滑函数,能够使用梯度下降法优化。然而当预测值距离真实值越远时,平方损失函数的惩罚力度越大,因此对异常点比较敏感。
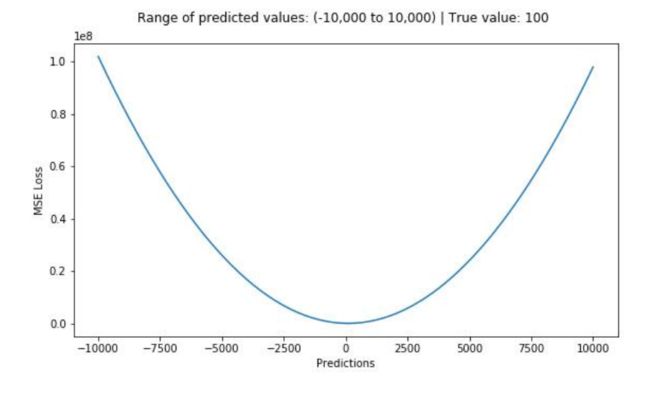
均方误差(MSE)是最常用的回归损失函数,计算方法是求预测值与真实值之间距离的平方和
(2)Absolute损失:![]()
绝对损失函数相当于在做中值回归,相比做均值回归的平方损失函数,绝对损失函数对异常点更鲁棒。但是,绝对损失函数在f=y处无法求导。
平均绝对误差(MAE)是另一种用于回归模型的损失函数。MAE是目标值和预测值之差的绝对值之和。其只衡量了预测值误差的平均模长,而不考虑方向,取值范围也是从0到正无穷。
应当如何选择损失函数:
MSE对误差取了平方(令e=真实值-预测值),因此若e>1,则MSE会进一步增大误差。如果数据中存在异常点,那么e值就会很大,而e则会远大于|e|。因此,相对于使用MAE计算损失,使用MSE的模型会赋予异常点更大的权重,然而这就会降低模型的整体性能。如果训练数据被异常点所污染,那么MAE损失就更好用。
直观上可以这样理解:如果我们最小化MSE来对所有的样本点只给出一个预测值,那么这个值一定是所有目标值的平均值。但如果是最小化MAE,那么这个值,则会是所有样本点目标值的中位数。众所周知,对异常值而言,中位数比均值更加鲁棒,因此MAE对于异常值也比MSE更稳定。
然而MAE存在一个严重的问题:更新的梯度始终相同,也就是说,即使对于很小的损失值,梯度也很大。这样不利于模型的学习。为了解决这个缺陷,可以使用变化的学习率,在损失接近最小值时降低学习率。而MSE在这种情况下的表现就很好,即便使用固定的学习率也可以有效收敛。MSE损失的梯度随损失增大而增大,而损失趋于0时则会减小。这使得在训练结束时,使用MSE模型的结果会更精确。
根据不同情况选择损失函数:如果异常点代表很重要的异常情况,并且需要被检测出来,则应选用MSE损失函数。相反,如果只把异常值当作受损数据,则应选用MAE损失函数。总而言之,处理异常点时,L1损失函数更稳定,但它的导数不连续,因此求解效率较低。L2损失函数对异常点更敏感,但通过令其导数为0,可以得到更稳定的封闭解。
在某些情况下,上述两种损失函数都不能满足需求,最简单的办法是对目标变量进行变换。而另一种办法则是换一个损失函数,这就引出了下面要讲的第三种损失函数,即Huber损失函数。 平滑的平均绝对误差
Huber损失函数在|f-y|较小时为平方损失,在|f-y|较大的时采用线性损失,处处可导,且对异常点鲁棒。Huber损失对数据中的异常点没有平方误差损失那么敏感。它在0也可微分。本质上,Huber损失是绝对误差,只是在误差很小时,就变为平方误差。误差降到多小时变为二次误差由超参数δ(delta)来控制。当Huber损失在[0-δ,0+δ]之间时,等价为MSE,而在[-∞,δ]和[δ,+∞]时为MAE。
这里超参数delta的选择非常重要,因为这决定了与异常点的定义。当残差大于delta,应当采用L1(对较大的异常值不那么敏感)来最小化,而残差小于超参数,则用L2来最小化。
使用Huber损失的原因:
使用MAE训练神经网络最大的一个问题就是不变的大梯度,这可能导致在使用梯度下降快要结束时,错过了最小点。而对于MSE,梯度会随着损失的减小而减小,使结果更加精确。
在这种情况下,Huber损失就非常有用。它会由于梯度的减小而落在最小值附近。比起MSE,它对异常点更加鲁棒。因此,Huber损失结合了MSE和MAE的优点。但是,Huber损失的问题是我们可能需要不断调整超参数delta。
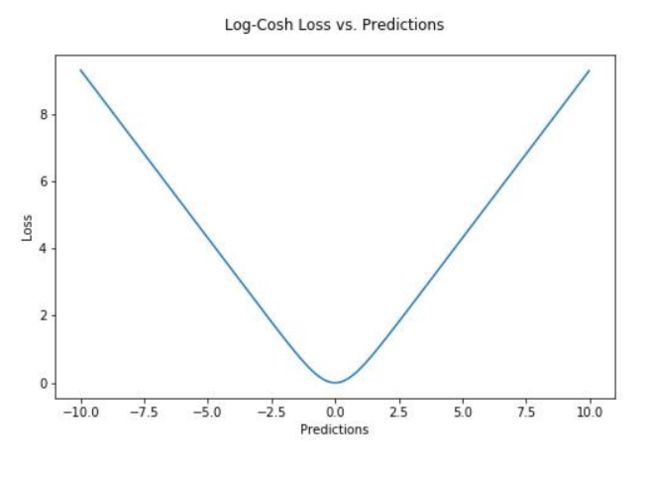
Log-cosh是另一种应用于回归问题中的,且比L2更平滑的的损失函数。它的计算方式是预测误差的双曲余弦的对数。
优点:对于较小的x,log(cosh(x))近似等于(x^2)/2,对于较大的x,近似等于abs(x)-log(2)。这意味着‘logcosh’基本类似于均方误差,但不易受到异常点的影响。它具有Huber损失所有的优点,但不同于Huber损失的是,Log-cosh二阶处处可微。
许多机器学习模型如XGBoost,就是采用牛顿法来寻找最优点。而牛顿法就需要求解二阶导数(Hessian)。因此对于诸如XGBoost这类机器学习框架,损失函数的二阶可微是很有必要的。
但Log-cosh损失也并非完美,其仍存在某些问题。比如误差很大的话,一阶梯度和Hessian会变成定值,这就导致XGBoost出现缺少分裂点的情况。
上述损失函数的代码:
import torch
import torch.nn as nn
import numpy as np
torch.manual_seed(20)
mse_loss = nn.MSELoss()#平方损失函数
mae_loss = nn.L1Loss(reduction='mean')#中值损失
criterion = nn.SmoothL1Loss()#huber损失,结合了平方损失和绝对值损失的优点。
# huber loss,结合了平方损失和绝对值损失的优点。
def huber(true, pred, delta):
loss = np.where(np.abs(true-pred) < delta,0.5*((true-pred)**2),delta*np.abs(true - pred) - 0.5*(delta**2))
print(loss)
return np.mean(loss)
# logcosh loss 双曲余弦的对数损失
def logcosh(true, pred):
loss = torch.log(torch.cosh(pred - true))
return torch.mean(loss)
a = torch.autograd.Variable(torch.ones(3, 2))#torch.randn(100, 128, requires_grad=True)
b = torch.autograd.Variable(torch.tensor([[0, 1], [2, 3],[4,5]]))#torch.randn(100, 128, requires_grad=True)
print(a.size())
print(b.size())
loss = mse_loss(a, b)
loss1 = mae_loss(a, b)
loss2 = criterion(a, b.float())
loss3 = huber(a, b, 1)
loss4 = logcosh(a, b)
print('mse_loss',loss.item())
print('mae_loss',loss1.item())
print('SmoothL1Loss',loss2.item())
print('huber loss',loss3.item())
print('logcoshloss',loss4.item())运行结果:
torch.Size([3, 2])
torch.Size([3, 2])
[[0.5 0. ]
[0.5 1.5]
[2.5 3.5]]
mse_loss 5.166666507720947
mae_loss 1.8333333730697632
SmoothL1Loss 1.4166666269302368
huber loss 1.4166666269302368
logcoshloss 1.3015135526657104总结
loss函数的选取取决于输入标签数据的类型:若输入的是实数、无界的值,损失函数使用平方差;若输入标签是位矢量(分类标志),使用交叉熵更适合。此外预测值与真实值要采用同样的数据分布,以便于loss函数取得更佳的效果。