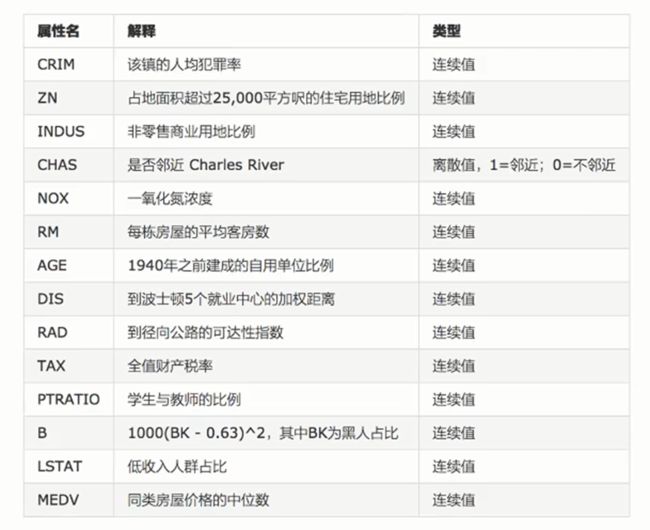
数据
导入包
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge, LogisticRegression, Lasso
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, classification_report, roc_auc_score
import joblib
import pandas as pd
import numpy as np
获取数据和标准化
lb = load_boston()
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25, random_state=1)
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.transform(y_test.reshape(-1, 1))
线性回归的正规方程求解
lr = LinearRegression()
lr.fit(x_train, y_train)
print('回归系数', lr.coef_)
y_predict = lr.predict(x_test)
y_lr_predict = std_y.inverse_transform(y_predict)
joblib.dump(lr, "./tmp/test.pkl")
print("正规方程测试集里面每个房子的预测价格:", y_lr_predict)
print("正规方程的均方误差:", mean_squared_error(y_test, y_predict))
结果:
回归系数 [[-0.12026411 0.15044778 0.02951803 0.07470354 -0.28043353 0.22170939
0.02190624 -0.35275513 0.29939558 -0.2028089 -0.23911894 0.06305081
-0.45259462]]
正规方程测试集里面每个房子的预测价格: [[32.37816533]
[27.95684437]
[18.07213891]
......
[21.16402252]
[26.00459084]]
正规方程的均方误差: 0.2758842244225052
正规方程inverse后的均方误差: 21.897765396049476
线性回归的梯度下降求解
sgd = SGDRegressor(eta0=0.008, penalty='l1', alpha=0.005)
sgd.fit(x_train, y_train)
print('梯度下降的回归系数', sgd.coef_)
y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test).reshape(-1, 1))
y_predict = sgd.predict(x_test)
print("梯度下降测试集里面每个房子的预测价格:", y_sgd_predict)
print("梯度下降的均方误差:", mean_squared_error(y_test, y_predict))
print("梯度下降的原始房价量纲均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
梯度下降的回归系数 [-0.09161381 0.07894594 -0.01997965 0.07736127 -0.18054122 0.26622108
0. -0.23891603 0.09441201 -0.02523685 -0.22153748 0.06690733
-0.4268276 ]
梯度下降测试集里面每个房子的预测价格: [[30.32788625]
[28.2472966 ]
[18.30943245]
[22.59556785]
......
[21.59354866]
[25.98775391]]
梯度下降的均方误差: 0.2782778128254135
梯度下降的原始房价量纲均方误差: 22.087751747792876
岭回归求解
rd = Ridge(alpha=0.05)
rd.fit(x_train, y_train)
print(rd.coef_)
y_predict = rd.predict(x_test)
y_rd_predict = std_y.inverse_transform(y_predict)
print("岭回归的均方误差:", mean_squared_error(y_test, y_predict))
print("岭回归的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_rd_predict))
[[-0.12019408 0.15027489 0.02932631 0.07472724 -0.28019156 0.22179958
0.0218258 -0.35250679 0.29879635 -0.20224632 -0.23906031 0.06305591
-0.45246484]]
岭回归的均方误差: 0.27588055100713926
岭回归的均方误差: 21.897473825960407
Lasso回归
ls = Lasso(alpha=0.05)
ls.fit(x_train, y_train)
print(ls.coef_)
y_predict = ls.predict(x_test)
y_ls_predict = std_y.inverse_transform(y_predict.reshape(-1,1))
print("Lasso回归的均方误差:", mean_squared_error(y_test, y_predict))
print("Lasso回归的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_ls_predict))
[-0.02365963 0. -0. 0.04558048 -0.03498273 0.25429207
-0. -0.02930847 0. -0. -0.18612471 0.02840277
-0.43680997]
Lasso回归的均方误差: 0.34915312700364426
Lasso回归的均方误差: 27.71333982009004
