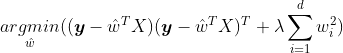多元线性回归详解
入门小菜鸟,希望像做笔记记录自己学的东西,也希望能帮助到同样入门的人,更希望大佬们帮忙纠错啦~侵权立删。
目录
一、问题描述
二、问题分析
三、解决问题 —— 找w和b
1、向量形式变换
2、目标式
3、导数为0得出结论
4、最终模型结果
四、潜藏的问题——可能不是满秩矩阵
五、潜藏问题解决方法——正则化
1、L1正则化——Lasso回归
2、L2正则化——岭回归
六、线性回归的变化与应用
七、python实现
1、多元线性回归
2、岭回归
3、lasso回归
八、线性模型——回归问题分类问题
一、问题描述
我们现在手头上有一个数据集D:每一个样本都由d个属性来描述,即 ![]() ,其中
,其中![]() 是样本x在第i个属性上的取值。而每个样本
是样本x在第i个属性上的取值。而每个样本![]() 最终对应的结果值为
最终对应的结果值为![]() 。
。
现在来了一个新的样本![]() ,想知道它的结果值
,想知道它的结果值![]()
二、问题分析
我们需要根据数据集D来找到一个线性模型来进行以![]() 预测
预测![]() ,即找到
,即找到![]() 中合适的w和b。
中合适的w和b。
三、解决问题 —— 找w和b
我们可以使用最小二乘法来解决这个问题。
1、向量形式变换
首先把w和b合成一个向量形式![]() ,大小为(d+1)* 1;
,大小为(d+1)* 1;
然后对标记y也写成向量模式: ![]()
2、目标式
![]()
令 ![]()
3、导数为0得出结论
4、最终模型结果
![]()
![]()
四、潜藏的问题—— 可能不是满秩矩阵
可能不是满秩矩阵
![]() 可能不是满秩矩阵,会产生多个
可能不是满秩矩阵,会产生多个![]() 最优解,该选择哪个解作为
最优解,该选择哪个解作为![]()
比如说:样本数较小,特征属性多,甚至已经超过样本数了,那么此时
不是满秩矩阵,可以解出多个
的解。
五、潜藏问题解决方法——正则化
正则化的作用是选择经验风险与模型复杂度同时较小的模型
1、L1正则化——Lasso回归
第一项是上述所说的经验风险,第二项控制的是模型的复杂度。
其中![]() ,控制惩罚力度:
,控制惩罚力度:![]() ;
;![]()
这也被称为Lasso回归。
如下图所示(假设只有两个属性):L1正则化平方误差项等值线和正则化等值线常相交于坐标轴上,这就意味着舍弃了其中某个属性,体现了特征选择的特性,更易得到稀疏解(相较于下面的L2正则化)—— 即求得的W向量中会有更少的非零值 。
2、L2正则化——岭回归
这也被称为岭回归。
L2正则化均匀选择参数,让拟合曲线各项系数都差不多,虽然没能减少项的个数,但是均衡了各项系数,这是原理上与L1正则化不同的地方。
六、线性回归的变化与应用
如果该问题的模型不是线性回归,则可尝试令模型预测值逼近y的衍生物。
比如——对数线性回归 ![]()
更一般的:![]() ,这称为广义线性模型。
,这称为广义线性模型。
七、python实现
1、多元线性回归
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X_train,X_test,Y_train,Y_test=train_test_split(x,y,test_size=0.3,random_state=1)//x,y分别为已经分好的属性数据和标记数据
model = LinearRegression()
model.fit(X_train, Y_train)
score = model.score(X_test, Y_test)
print('模型测试得分:'+str(score))
Y_pred = model.predict(X_test)
print(Y_pred)2、岭回归
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
X_train,X_test,Y_train,Y_test=train_test_split(x,y,test_size=0.3,random_state=1)//x,y分别为已经分好的属性数据和标记数据
model = Ridge(alpha=1)
model.fit(X_train, Y_train)
score = model.score(X_test, Y_test)
print('模型测试得分:'+str(score))
Y_pred = model.predict(X_test)
print(Y_pred)3、lasso回归
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
X_train,X_test,Y_train,Y_test=train_test_split(x,y,test_size=0.3,random_state=1)//x,y分别为已经分好的属性数据和标记数据
model = Lasso(alpha=0.1)
model.fit(X_train, Y_train)
score = model.score(X_test, Y_test)
print('模型测试得分:'+str(score))
Y_pred = model.predict(X_test)
print(Y_pred)八、线性模型——回归问题 分类问题
分类问题
上述说的都是用线性模型解决回归问题,其实线性模型也可以用来解决分类问题——逻辑回归(对数几率回归)。
详见逻辑回归(Logistic Regression)_tt丫的博客-CSDN博客_逻辑回归csdn
欢迎大家在评论区批评指正,谢谢大家~