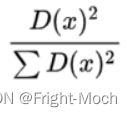基于数据挖掘的入侵检测系统实验

一、实验背景及意义：

数据挖掘算法可以挖掘隐藏于大数据中的信息。入侵数据也具有大数据的特点，数据挖掘的许多方法可以应用于入侵检测，如聚类、分类、关联分析、序列分析方法。

“物以类聚，人与群分”即为聚类的通俗理解。聚类将数据按相似性的原则进行分类，分类后的类别称为簇；每个簇内有很大的相似性，而不同簇之间有很大的相异性。聚类是将物理或抽象对象的集合划分成多个类的过程，每一类都由相似的对象组成。聚类分析也是无监督学习的过程；与分类不同，在学习的过程不依赖于预先定义的类或带类标记的训练集，而是通过自身算法进行分类成簇。若将聚类分析应用在入侵检测中，一般假设正常行为的数目远远大于入侵行为的数目；同时，假设入侵行为和正常行为的差异很大。

聚类分析是在未知世界中进行探索性分析。聚类分析只要根据给定的聚类个数就可以自动进行分类。因此，聚类分析也受聚类个数的影响，不同的聚类个数将会影响聚类效果，个数的确定也成为聚类分析的一个关键变量。事实上，用来计算聚类之间距离的方法也非常多，通常按照数据和分析的不同目的要求来选择距离公式。常用的距离公式有欧氏距离(Euclidean distance) 、曼哈顿距离(Block)、切比雪夫距离(Chebychev distance)等。

二、实验环境：

一台Windows 主机、Python3、scikit-learn、matplotlib、KDD Cup 1999 数据集、pycharm

三、实验目的：

（1）学习并理解K-Means思想和实现流程。

（2）通过本次实验，掌握K-Means算法如何聚类攻击类型，并通过python编程实现，以更好地实现针对性的防御。

四、实验要求：

（一）、聚类算法的环境搭建：

首先在windows系统中新建用户。然后在windows主机上安装Python38，将目录C:\Program Files\Python38和C:\Program Files\Python38\Scripts添加到系统变量Path之后。接着在CMD里输入命令：pip install sklearn -i https://pypi.doubanio.com/simple，安装机器学习包sklearn。输入命令：pip install matplotlib -i https://pypi.doubanio.com/simple，安装绘图工具matplotlib。输入命令：pip install numpy -i https://pypi.doubanio.com/simple，安装科学计算工具。输入命令：pip install pandas -i https://pypi.doubanio.com/simple，安装数据分析工具包。

（二）、理解K-Means和x-means算法：

1、简要理解K-Means算法

K-means源于信号处理中的一种向量量化方法，是一种聚类算法，更多应用于数据挖掘领域。其中K表示簇数或类别数，既假设簇划分为(C1,C2,...,Ck)；Means表示均值。因此，K-Means是一种通过均值对数据点进行聚类的算法。K-Means算法通过预先设定的K值及每个类别的初始质心，接着对相似的数据点进行划分；并通过划分后的均值，不断迭代优化，以获得最优的聚类结果。最终使得目标最小。

基于可视化方法解释K-means算法如图1所示：

伪代码：

获取数据 n 个 m 维的数据

随机生成 K 个 m 维的点

while(t)

    for(int i=0;i < n;i++)

        for(int j=0;j < k;j++)

            计算点 i 到类 j 的距离

    for(int i=0;i < k;i++)

        1. 找出所有属于自己这一类的所有数据点

        2. 把自己的坐标修改为这些数据点的中心点坐标

end

因此，该算法的时间复杂度为

其中，t 为迭代次数，k 为簇的数目，n 为样本点数，m 为样本点维度。空间复杂度：，其中，k 为簇的数目，m 为样本点维度，n 为样本点数。

1. K-means优点：

1. 算法快速、简单。
2. 当聚类是密集的，且类与类之间区别明显时，效果较好。
3. 算法复杂度低。

1. K-means缺点：

1. 它的计算规模是受限的。
2. K值需要人为设定，不同K值得到的结果不一样；
3. 对初始的簇中心敏感，不同选取方式会得到不同结果；
4. 对异常值敏感；
5. 它的搜索是基于局部极小值的。
6. 不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类。
7. 样本只能归为一类，不适合多分类任务；

2、K-means++

既然K-means初始值的选取对结果的影响很大，对初始值选择的改进是很重要的一部分。在所有的改进算法中，K-means++ 最有名。K-means++ 算法步骤如下所示：

1. 随机选取一个中心点a1；
2. 计算每个数据到已有聚类中心最远的距离D(X)  ，并以一定概率
     选择新中心点a1；
3. 重复第二步。

选出初始点后，就继续使用标准的 k-means 算法。简单的来说，就是 K-means++ 就是选择离已选聚类中心点最远的点。这也比较符合常理，聚类中心当然是互相离得越远越好。但是这个算法的缺点在于，难以并行化。

（三）、使用K-Means算法聚类攻击类型：

1、KDD Cup 1999 数据集概述

1998年美国国防部高级规划署（DARPA）在MIT林肯实验室进行的一项入侵检测评估项目。林肯实验室建立了模拟美国空军局域网的一个网络环境，仿真模拟了各种用户类型、各种不同的网络流量和攻击手段，使它就像一个真实的网络环境，收集了9周时间的 TCPdump网络连接和系统审计数据。该数据为KDD Cup 1999 数据集。这些TCPdump采集的原始数据被分为两个部分：

（1）7周时间的训练数据大概包含5000000多个网络连接记录。

（2）剩下2周时间的测试数据大概包含2000000个网络连接记录。

该数据集中一个网络连接定义为：在某个时间内从开始到结束的TCP数据包序列。并且在这段时间内，数据在预定义的协议（如TCP、UDP）下，从源IP地址到目的IP地址的传递。每个网络连接被标记为正常（normal）或异常（attack）；异常类型被细分为4大类共39种攻击类型，其中22种攻击类型出现在训练集中，另有17种未知攻击类型出现在测试集中。

KDD99数据集中每个连接（*）用41个特征来描述，保存为CSV格式，加上最后的标记（label），一共有42项，其中前41项特征分为4大类。数据集如图所示：

2、理解KDD Cup 1999 数据集的特征

下面按顺序解释各个特征的含义。其中，（*）一条连接记录的定义是：一个完整的TCP连接会话，或一个UDP数据包或一个ICMP数据包。（**）“compromised condition”为目标系统出现不正常的状态，例如文件或路径“not found”，或使用“jump to” 跳转指令等。（***）”host”列表为授权用户列表。

2.1、TCP连接基本特征（共9种）

其中基本连接特征包含了一些连接的基本属性，如连续时间，协议类型，传送的字节数等，具体含义如下：

（1）duration. 连接持续时间，以秒为单位，连续类型。范围是 [0, 58329] 。它的定义是从TCP连接以3次握手建立算起，到FIN/ACK连接结束为止的时间；若为UDP协议类型，则将每个UDP数据包作为一条连接。数据集中出现大量的duration = 0的情况，是因为该条连接的持续时间不足1秒。

（2）protocol_type. 协议类型，离散类型，共有3种：TCP, UDP, ICMP。

（3）service. 目标主机的网络服务类型，离散类型，共有70种。’aol’, ‘auth’, ‘bgp’, ‘courier’,‘csnet_ns’, ‘ctf’, ‘daytime’, ‘discard’, ‘domain’, ‘domain_u’, ‘echo’, ‘eco_i’,‘ecr_i’, ‘efs’, ‘exec’, ‘finger’, ‘ftp’, ‘ftp_data’, ‘gopher’, ‘harvest’,‘hostnames’, ‘http’, ‘http_2784′, ‘http_443′, ‘http_8001′, ‘imap4′, ‘IRC’,‘iso_tsap’, ‘klogin’, ‘kshell’, ‘ldap’, ‘link’, ‘login’, ‘mtp’, ‘name’,‘netbios_dgm’, ‘netbios_ns’, ‘netbios_ssn’, ‘netstat’, ‘nnsp’, ‘nntp’, ‘ntp_u’,‘other’, ‘pm_dump’, ‘pop_2′, ‘pop_3′, ‘printer’, ‘private’, ‘red_i’,‘remote_job’, ‘rje’, ‘shell’, ‘smtp’, ‘sql_net’, ‘ssh’, ‘sunrpc’, ‘supdup’,‘systat’, ‘telnet’, ‘tftp_u’, ‘tim_i’, ‘time’, ‘urh_i’, ‘urp_i’, ‘uucp’,‘uucp_path’, ‘vmnet’, ‘whois’, ‘X11′, ‘Z39_50′。

（4）flag. 连接正常或错误的状态，离散类型，共11种。’OTH’, ‘REJ’, ‘RSTO’, ‘RSTOS0′,‘RSTR’, ‘S0′, ‘S1′, ‘S2′, ‘S3′, ‘SF’, ‘SH’。它表示该连接是否按照协议要求开始或完成。例如SF表示连接正常建立并终止；S0表示只接到了SYN请求数据包，而没有后面的SYN/ACK。其中SF表示正常，其他10种都是error。

（5）src_bytes. 从源主机到目标主机的数据的字节数，连续类型，范围是 [0,1379963888]。

（6）dst_bytes. 从目标主机到源主机的数据的字节数，连续类型，范围是 [0.1309937401]。

（7）land. 若连接来自/送达同一个主机/端口则为1，否则为0，离散类型，0或1。

（8）wrong_fragment. 错误分段的数量，连续类型，范围是 [0, 3]。

（9）urgent. 加急包的个数，连续类型，范围是[0, 14]。

2.2、 TCP连接的内容特征（共13种）

对于U2R（User-to-Root）和R2L（Remote-to-Login）之类的攻击，由于它们不像DoS攻击那样在数据记录中具有频繁序列模式，而一般都是嵌入在数据包的数据负载里面；因此，单一的数据包和正常连接没有什么区别。为了检测这类攻击，可以从数据内容里面抽取部分可能反映入侵行为的内容特征，如登录失败的次数等。

（10）hot. 访问系统敏感文件和目录的次数，连续类型，范围是 [0, 101]。例如访问系统目录，建立或执行程序等。

（11）num_failed_logins. 登录尝试失败的次数，连续类型，[0, 5]。

（12）logged_in. 成功登录则为1，否则为0，离散类型，0或1。

（13）num_compromised.  “妥协”条件（**）出现的次数，连续类型，[0, 7479]。

（14）root_shell. 若获得root shell 则为1，否则为0，离散类型，0或1。root_shell是指获得超级用户权限。

（15）su_attempted. 若出现“su root“ 命令则为1，否则为0，离散类型，0或1。

（16）num_root. root用户访问次数，连续类型，[0, 7468]。

（17）num_file_creations. 文件创建操作的次数，连续类型，[0, 100]。

（18）num_shells. 使用shell命令的次数，连续类型，[0, 5]。

（19）num_access_files. 访问关键文件的次数，连续类型，[0, 9]。例如对 /etc/passwd 或 .rhosts 文件的访问。

（20）num_outbound_cmds. 一个FTP会话中出站命令数，连续类型，0。数据集中这一特征出现次数为0。

（21）is_host_login. 登录是否属于“host”列表，是为1，否则为0，离散类型，0或1。例如超级用户或管理员登录。

（22）is_guest_login. 若是guest 登录则为1，否则为0，离散类型，0或1。

2.3、 基于时间的网络流量统计特征（共9种，23～31）

由于网络攻击事件在时间上有很强的关联性；因此，统计出当前连接记录与之前一段时间内的连接记录之间存在的某些联系，可以更好的反映连接之间的关系。这类特征又分为两种集合：一个是 “same host”特征，只观察在过去两秒内与当前连接有相同目标主机的连接，例如相同的连接数，这些相同连接与当前连接是否有相同服务的连接等；另一个是 “same service”特征，只观察过去两秒内与当前连接有相同服务的连接，例如这样的连接有多少个，其中有多少出现SYN错误或者REJ错误。

（23）count. 过去两秒内，与当前连接具有相同的目标主机的连接数，连续类型，[0, 511]。

（24）srv_count. 过去两秒内，与当前连接具有相同服务的连接数，连续类型，[0, 511]。

（25）serror_rate. 过去两秒内，在与当前连接具有相同目标主机的连接中，出现“SYN” 错误的连接的百分比，连续类型，[0.00, 1.00]。

（26）srv_serror_rate. 过去两秒内，在与当前连接具有相同服务的连接中，出现“SYN” 错误的连接的百分比，连续类型，[0.00, 1.00]。

（27）rerror_rate. 过去两秒内，在与当前连接具有相同目标主机的连接中，出现“REJ” 错误的连接的百分比，连续类型，[0.00, 1.00]。

（28）srv_rerror_rate. 过去两秒内，在与当前连接具有相同服务的连接中，出现“REJ” 错误的连接的百分比，连续类型，[0.00, 1.00]。

（29）same_srv_rate. 过去两秒内，在与当前连接具有相同目标主机的连接中，与当前连接具有相同服务的连接的百分比，连续类型，[0.00, 1.00]。

（30）diff_srv_rate. 过去两秒内，在与当前连接具有相同目标主机的连接中，与当前连接具有不同服务的连接的百分比，连续类型，[0.00, 1.00]。

（31）srv_diff_host_rate. 过去两秒内，在与当前连接具有相同服务的连接中，与当前连接具有不同目标主机的连接的百分比，连续类型，[0.00, 1.00]。

注：这一大类特征中，23、25、27、29、30这5个特征是 “samehost” 特征，前提都是与当前连接具有相同目标主机的连接；24、26、28、31这4个特征是 “same service” 特征，前提都是与当前连接具有相同服务的连接。

2.4、 基于主机的网络流量统计特征（共10种，32～41）

基于时间的流量统计只是在过去两秒的范围内统计与当前连接之间的关系；而在实际入侵中，有些Probing攻击使用慢速攻击模式来扫描主机或端口，当它们扫描的频率大于2秒的时候，基于时间的统计方法就无法从数据中找到关联。因此可以按照目标主机进行分类，使用一个具有100个连接的时间窗，统计当前连接之前100个连接记录中与当前连接具有相同目标主机的统计信息。

（32）dst_host_count. 前100个连接中，与当前连接具有相同目标主机的连接数，连续类型，[0, 255]。

（33）dst_host_srv_count. 前100个连接中，与当前连接具有相同目标主机相同服务的连接数，连续类型，[0, 255]。

（34）dst_host_same_srv_rate. 前100个连接中，与当前连接具有相同目标主机相同服务的连接所占的百分比，连续类型，[0.00, 1.00]。

（35）dst_host_diff_srv_rate. 前100个连接中，与当前连接具有相同目标主机不同服务的连接所占的百分比，连续类型，[0.00, 1.00]。

（36）dst_host_same_src_port_rate. 前100个连接中，与当前连接具有相同目标主机相同源端口的连接所占的百分比，连续类型，[0.00, 1.00]。

（37）dst_host_srv_diff_host_rate. 前100个连接中，与当前连接具有相同目标主机相同服务的连接中，与当前连接具有不同源主机的连接所占的百分比，连续类型，[0.00, 1.00]。

（38）dst_host_serror_rate. 前100个连接中，与当前连接具有相同目标主机的连接中，出现SYN错误的连接所占的百分比，连续类型，[0.00, 1.00]。

（39）dst_host_srv_serror_rate. 前100个连接中，与当前连接具有相同目标主机相同服务的连接中，出现SYN错误的连接所占的百分比，连续类型，[0.00, 1.00]。

（40）dst_host_rerror_rate. 前100个连接中，与当前连接具有相同目标主机的连接中，出现REJ错误的连接所占的百分比，连续类型，[0.00, 1.00]。

（41）dst_host_srv_rerror_rate. 前100个连接中，与当前连接具有相同目标主机相同服务的连接中，出现REJ错误的连接所占的百分比，连续类型，[0.00, 1.00]。

3、轮廓系数概述

实现聚类的一个重要的问题就是需要确定聚类的个数。普通人不可能手动检查数据以找到适当数量的聚类；因此，需要使用某种方法来估计聚类的数量，并确保在这个数量下进行聚类的效果比较好。

本实验将使用轮廓分析(silhouette analysis)法，通过图形工具来度量簇中样本的聚集程度。通过三个步骤可以计算出单个样本的轮廓系数(silhouette coefficient)：

1. 将样本xi与簇内的其他点之间的平均距离作为簇内的内聚度ai
2. 将样本xi与最近簇中所有点之间的平均距离看作是与最近簇的分离度bi
3. 将簇的分离度bi与簇内聚度ai之差除以二者中比较大的数得到轮廓系数，计算公式（1）如下     

轮廓系数的取值在-1到1之间。当簇内聚度与分度离相等时，轮廓系数为0。当b>>a时，轮廓系数近似取到1，此时模型的性能最佳。

本实验针对KDD Cup 1999 数据集进行测试。首先需要指定聚类数量；然后画出轮廓图，通过轮廓图可以看出样本的簇数，并判断样本中是否包含异常值。为了评价聚类模型的性能，可以通过轮廓系数平均值来评价模型性能（既下图3中出现的红色虚线进行评价）。

4、计算轮廓系数，评价模型性能

4.1 k-means++聚类KDD Cup 1999 数据

首先新建kmeans_plus_silhouette_coefficient.py文件，并在文件中写入如下代码：

from os import environ
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
#消除警告
def suppress_qt_warnings():
    environ["QT_DEVICE_PIXEL_RATIO"] = "0"
    environ["QT_AUTO_SCREEN_SCALE_FACTOR"] = "1"
    environ["QT_SCREEN_SCALE_FACTORS"] = "1"
    environ["QT_SCALE_FACTOR"] = "1"
suppress_qt_warnings()
plt.rcParams['font.sans-serif']=['SimHei']    # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False    # 用来正常显示负号
# Cluster number using k-means.
CLUSTER_NUM = 5
# Dataset path.
dataset_dir = os.path.join(os.path.dirname(os.path.abspath(__file__)), './dataset')
dataset_path = os.path.join(dataset_dir, 'kddcup.data_small.csv')
# Load data.
df_kddcup = pd.read_csv(dataset_path)
df_kddcup = df_kddcup.iloc[:, [0, 7, 10, 11, 13, 35, 37, 39]]
# Normalization.
df_kddcup = (df_kddcup - df_kddcup.mean()) / df_kddcup.std()
# Transpose of matrix.
kddcup_array = np.array([df_kddcup['duration'].tolist(),
                      df_kddcup['wrong_fragment'].tolist(),
                      df_kddcup['num_failed_logins'].tolist(),
                      df_kddcup['logged_in'].tolist(),
                      df_kddcup['root_shell'].tolist(),
                      df_kddcup['dst_host_same_src_port_rate'].tolist(),
                      df_kddcup['dst_host_serror_rate'].tolist(),
                      df_kddcup['dst_host_rerror_rate'].tolist(),
                      ], float)
kddcup_array = kddcup_array.T
km = KMeans(n_clusters=2,init="k-means++",n_init=10,max_iter=300,tol=1e-4,random_state=0)
y_km = km.fit_predict(kddcup_array)

其中KMeans函数中的n_clusters参数可以控制聚类数量。在代码df_kddcup = df_kddcup.iloc[:, [0, 7, 10, 11, 13, 35, 37, 39]]中，iloc通过行号0, 7, 10, 11, 13, 35, 37, 39来索引行数据。他们是用于判断攻击类型比较重要的指标，所以把他们作为聚类的特征。在kdd数据集中分别代表的是：

1. duration ：与主机的连接时间（秒）。
2. wrong_fragment ：不正确的片段数。
3. num_failed_logins ：登录尝试失败的次数。
4. login_in ：成功登录。
5. root_shell ：获取根shell。
6. dst_host_same_src_port_rate ：同一端口的连接速率。
7. dst_host_serror_rate：SYN错误率。

dst_host_rerror_rate：REJ错误率。

4.2 计算并可视化轮廓系数代码

继续在kmeans_plus_silhouette_coefficient.py文件后写入如下代码：

import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples
#获取簇的标号
cluster_labels = np.unique(y_km)
#获取簇的个数
n_clusters = cluster_labels.shape[0]
#基于欧式距离计算轮廓系数
silhoutte_vals = silhouette_samples(kddcup_array,y_km,metric="euclidean")
#设置y坐标的起始位置
y_ax_lower,y_ax_upper=0,0
yticks=[]
for i,c in enumerate(cluster_labels):
    #获取不同簇的轮廓系数
    c_silhouette_vals = silhoutte_vals[y_km == c]
    #对簇中样本的轮廓系数由小到大进行排序
    c_silhouette_vals.sort()
    #获取到簇中轮廓系数的个数
    y_ax_upper += len(c_silhouette_vals)
    #获取不同颜色
    color = cm.jet(i / n_clusters)
	#绘制水平直方图
    plt.barh(range(y_ax_lower,y_ax_upper),c_silhouette_vals,
            height=1.0,edgecolor="none",color=color)
    #获取显示y轴刻度的位苴
    yticks.append((y_ax_lower+y_ax_upper) / 2)
    #下一个y轴的起点位置
    y_ax_lower += len(c_silhouette_vals)
#获取轮廓系数的平均值
silhouette_avg = np.mean(silhoutte_vals)
#绘制一条平行y轴的轮廓系数平均值虚线
plt.axvline(silhouette_avg,color="red",linestyle="--")
#设置y轴显示的刻度
plt.yticks(yticks,cluster_labels+1)
plt.ylabel("簇")
plt.xlabel("轮廓系数")
plt.show()

4.3 n_cluster=2的轮廓系数

此时运行python kmeans_plus_silhouette_coefficient.py，效果如图所示：

由于轮廓系数是一个衡量一个结点它所属聚类相较于其它聚类的相似程度，取值范围为-1到1；轮廓系数的值越大表明这个结点更匹配其属聚类而不与相邻的聚类匹配。如果大多数节点都有很高的轮廓系数，那么聚类适当。若许多点都有低值或负值，说明分类过多或者过少。从图3中可以看到， “轮廓系数”远非1，轮廓的宽度相差很大。因此，将聚类数设置为2似乎不合适。

4.4 n_cluster=3的轮廓系数

将KMeans函数的n_clusters参数值设置为3，此时运行python kmeans_plus_silhouette_coefficient.py，效果如图所示：

 cluster1的“轮廓系数”接近1，而cluste2和cluster3还远远没达到。且轮廓的宽度仍有很大差异。因此，将群集数设置为3似乎不合适

4.5 n_cluster=4的轮廓系数

将KMeans函数的n_clusters参数值设置为4，此时运行python kmeans_plus_silhouette_coefficient.py，效果如图所示：

它已经变得相当不错。但是，由于cluster2的轮廓宽度较大，因此似乎可以做更多的聚类

4.6 n_cluster=5的轮廓系数

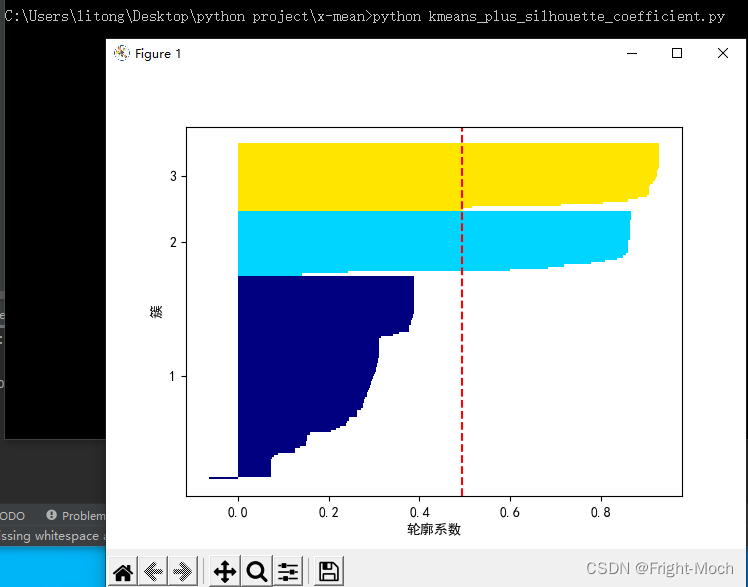
将KMeans函数的n_clusters参数值设置为5，此时运行python kmeans_plus_silhouette_coefficient.py，效果如图所示：

图6中， 看到4个簇的“轮廓系数”接近1，轮廓的宽度几乎均匀。显示目前最好的形状。因此，将群集数设置为5似乎是合适的

1. n_cluster=6的轮廓系数

将KMeans函数的n_clusters参数值设置为6，此时运行python kmeans_plus_silhouette_coefficient.py，效果如图所示：

在图7中，“轮廓系数”的变化很小；另外，我们看到cluster5和cluster6的轮廓宽度非常小；因此，似乎过度地将它们划分为簇。所以，将群集数设置为6是不合适的。实验至此，我们可以确定k-means聚类数为5是比较合适的。

5、分析K-Means聚类的代码

5.1 首先导入相关库

导入的库含scikit-learn的K-means，且包含了各种用于执行K均值的类。为了可视化聚类结果，还导入了图形绘制库matplotlib。新建文件kmeans_plus_plot.py，在该文件中写入如下代码：

import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

5.2 设置聚类数为5

在kmeans_plus_plot.py文件后继续写入如下代码：

CLUSTER_NUM = 5

5.3 加载数据集

在kmeans_plus_plot.py文件后继续写入如下代码：

# Dataset path.
dataset_dir = os.path.join(os.path.dirname(os.path.abspath(__file__)), './dataset')
dataset_path = os.path.join(dataset_dir, 'kddcup.data_small.csv')
# Load data.
df_kddcup = pd.read_csv(dataset_path)
df_kddcup = df_kddcup.iloc[:, [0, 7, 10, 11, 13, 35, 37, 39]]

5.4 归一化

然后对每个特征的数据值进行归一化以提高分析准确性。在kmeans_plus_plot.py文件后继续写入如下代码：

df_kddcup = (df_kddcup - df_kddcup.mean()) / df_kddcup.std()

5.5 对数据进行矩阵转置

由于fit_predict函数会使用矩阵作为参数，所以将读取的数据转换为numpy矩阵。在kmeans_plus_plot.py文件后继续写入如下代码：

kddcup_array = np.array([df_kddcup['duration'].tolist(),
                      df_kddcup['wrong_fragment'].tolist(),
                      df_kddcup['num_failed_logins'].tolist(),
                      df_kddcup['logged_in'].tolist(),
                      df_kddcup['root_shell'].tolist(),
                      df_kddcup['dst_host_same_src_port_rate'].tolist(),
                      df_kddcup['dst_host_serror_rate'].tolist(),
                      df_kddcup['dst_host_rerror_rate'].tolist(),
                      ], float)
kddcup_array = kddcup_array.T

5.6 K-Means聚类

使用scikit-learn的K-Means类创建一个k-means模型，然后将转置后的矩阵传给fit_predict进行聚类。在kmeans_plus_plot.py文件后继续写入如下代码：

# Clustering.
pred = KMeans(n_clusters=CLUSTER_NUM).fit_predict(kddcup_array)
df_kddcup['cluster_id'] = pred
print(df_kddcup)
print(df_kddcup['cluster_id'].value_counts())

5.7 可视化聚类结果

使用matplotlib画出堆积条形图。在kmeans_plus_plot.py文件后继续写入如下代码：

cluster_info = pd.DataFrame()
for i in range(CLUSTER_NUM):
    cluster_info['cluster' + str(i)] = df_kddcup[df_kddcup['cluster_id'] == i].mean()
cluster_info = cluster_info.drop('cluster_id')
kdd_plot = cluster_info.T.plot(kind='bar', stacked=True, title="Mean Value of Clusters")
kdd_plot.set_xticklabels(kdd_plot.xaxis.get_majorticklabels(), rotation=0)
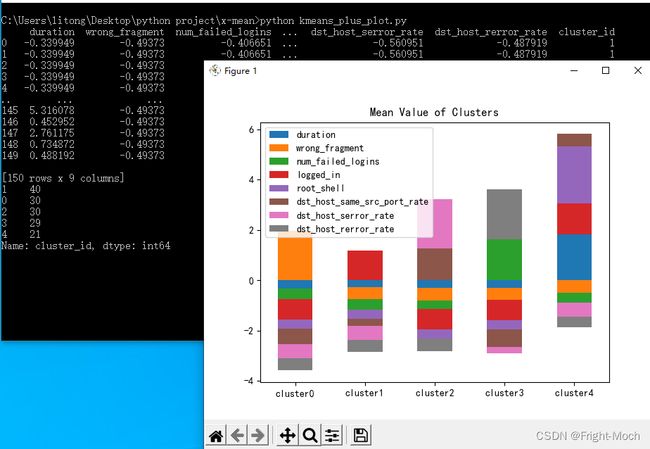
plt.show()

此时输入python kmeans_plus_plot.py，效果如图所示

 可以看到数据已经聚成5类，并且每个类中包含的数据的组成部分都以彩色显示。

5.8 可视化聚类结果分析

根据每个类的组成，每个类代表什么呢？

1. 1. Cluster0:在这一类可以看到“ wrong_fragment”（错误片段的数量）大于其他类。鉴于有许多“wrong_fragement”，我们有理由推测它是“teardrop”攻击的类
   2. Cluster1:相对于其他聚类来说，可以看到每种颜色的组成比率都是差不多的，这应该是正常的网络通信
   3. Cluster2: 可以看到，“ dst_host_serror_rate”（SYN错误率）和“dst_host_same_src_port_rate”（到同一端口的连接率）的组成比率大于其他类。基于“高SYN错误率”和“到同一端口的更多连接”等功能，我们可以推测是这是“Nmap扫描”或”SYN Flood “攻击的类。
   4. Cluster3:可以看到，dst_host_rerror_rate（出现REJ错误的连接所占的百分比）和num_failed_logins（失败的登录尝试次数）的组成比率大于其他类。基于高REJ错误率和大量失败登录尝试等功能，我们猜测这是一个“爆破密码”攻击的类
   5. Cluster4:可以看到，“ root_shell”（紫色，表示取得root shell）和“ duration”（蓝色，表示与主机的连接时间）的组成比率都比其他类的大。基于“与主机的连接时间长”和“在许多情况下具有root特权”的功能，我们推测这是一个“缓冲区溢出”攻击的类。

因此，通过K-means方法分析“kddcup.data_small.csv”，可能存在4种攻击类型；这四种攻击类型分别是缓冲区溢出、Nmap 扫描/ SYN Flood、密码暴力破解、Teardrop。防守方通过分析得出的结果，就可以识别出攻击手段，以采取专门的防护措施进行防御。

参考资料

1. https://zhuanlan.zhihu.com/p/78798251
2. https://www.bbsmax.com/A/q4zVZl1jzK/
3. https://blog.csdn.net/u012679583/article/details/80316619
4. https://zhuanlan.zhihu.com/p/150266277
5. https://github.com/13o-bbr-bbq/machine_learning_security
6. https://juejin.im/post/6844904135741931533
7. Dan P, Moore A W. X-means: Extending K-means with Efficient Estimation of the Number of Clusters[C]. Seventeenth International Conference on Machine Learning. Morgan Kaufmann Publishers Inc. 2000:727-734.
8. https://github.com/hellowuzekai/BotMiner-x
9. https://wenku.baidu.com/view/6c2b3eac33d4b14e84246827.html
10. Gu G, Perdisci R, Zhang J, et al. BotMiner: Clustering Analysis of Network Traffic for Protocol-and Structure-Independent Botnet Detection.[J]. Proceedings of Usenix Security Symposium, 2008:139-154.