机器学习算法系列（二十）-梯度提升决策树算法（Gradient Boosted Decision Trees / GBDT）

阅读本文需要的背景知识点：自适应增强算法、泰勒公式、One-Hot编码、一丢丢编程知识

一、引言

  前面一节我们学习了自适应增强算法（Adaptive Boosting / AdaBoost Algorithm），是一种提升算法 （Boosting Algorithm），而该算法家族中还有另一种重要的算法——梯度提升决策树¹ （Gradient Boosted Decision Trees / GBDT），GBDT 及其变体算法在传统机器学习中有着广泛的应用，了解其背后的思想与原理对于以后的学习有很大的帮助。

二、模型介绍

  梯度提升决策树同自适应增强算法一样是一种提升算法，也可以解释为一种加法模型，第 k 轮后的强估计器为第 k - 1 轮后的强估计器加上带系数的弱估计器 h(x)：

$$H_k(x)=H_{k-1}(x)+{\alpha }_k{h}_k(x)$$

式2-1

  假设第 k - 1 轮对应的代价函数为$Cost(y,H_{k-1}(X))$, 第 k 轮对应的代价函数为$Cost(y,H_k(X))$，我们的目的是使得每次迭代后，其代价函数都会逐渐变小。
  由于每个不同的代价函数对应的优化方式不同，Jerome H. Friedman 在其原始算法的论文² 中给出了一个统一处理的方法，可以使用代价函数的负梯度来拟合该轮迭代代价函数的减小，这也是最速下降法的一种近似，其本质是使用一阶泰勒公式近似其代价函数。当基础估计器使用的是决策回归树时，该算法被称为梯度提升决策树（GBDT）。
$${\hat{y}}_{k,i}=-{\left[\frac{\partial Cost(y_i,H(X_i))}{\partial H(X_i)}\right]}_{H(x)=H_{k-1}(x)}$$

式2-2

  下面还是同 AdaBoost 算法一样，分别考虑回归、二分类、多分类这三个问题，一一介绍每个问题对应的算法。由于 GBDT 算法回归比分类简单，所以这次将回归问题放在前面介绍。

回归

  对于回归问题的代价函数，我们先使用平方误差来作为代价函数：
$$Cost(y,H(x))=(y-H(x){)}^2$$

式2-3

  第 k 轮的代价函数：
（1）带入式 2-1
（2）带入平方误差的代价函数
（3）改变括号
（4）将 y 与第 k - 1 轮的结果之差记为 ${\hat{y}}_k$
$$\begin{array}{rlr}Cost(y,H_k(x))& =Cost(y,H_{k-1}(x)+{\alpha }_k{h}_k(x))& (1)\\ & =(y-(H_{k-1}(x)+{\alpha }_k{h}_k(x)){)}^2& (2)\\ & =((y-H_{k-1}(x))-{\alpha }_k{h}_k(x){)}^2& (3)\\ & =({\hat{y}}_k-{\alpha }_k{h}_k(x){)}^2& (4)\end{array}$$

式2-4

  观察式 2-4 中的（4）式会发现这就是前面章节中介绍的决策回归树的代价函数，只是该回归树不再是使用训练集中的 y，而是去拟合上式中的 $\hat{y}$，也可以称为残差。得到回归树后更新 H(x) ，然后进行新的迭代。
  这样就得到了最简单的最小二乘回归的 GBDT 算法实现，具体步骤可以参考第三节的算法步骤中的回归部分，可以看到其中的系数 $\alpha$ 可以理解为融入到了回归树内部。
  在论文中作者还介绍了其他的几种代价函数，分别是最小绝对偏差（LDA）、Huber 损失³ 等，感兴趣的读者可以阅读论文中对应的章节。

  由于 GBDT 需要计算负梯度是个连续值，所以对于分类问题， 其基础估计器没有使用分类树，而是依然使用的回归树。

二分类

  对于分类问题的代价函数，可以使用指数函数与对数函数。当使用指数函数时，GBDT 将等同于前面一节中介绍的 AdaBoost 算法，这里我们使用对数函数作为代价函数：
$$Cost(y,H(x))=\log (1+e^{-2yH(x)})$$

式2-5

  按照前面模型介绍的计算负梯度的方法，带入代价函数计算出 $\hat{y}$ ：
$$\begin{array}{rlr}{\hat{y}}_{k,i}& =-{\left[\frac{\partial Cost(y_i,H(X_i))}{\partial H(X_i)}\right]}_{H(x)=H_{k-1}(x)}& (1)\\ & =\frac{2y_i}{1+e^{2y_i{H}_{k-1}(X_i)}}& (2)\end{array}$$

式2-6

  计算出 $\hat{y}$ 后我们可以拟合出一颗回归树估计器 h(x) ，这时我们要求的是每轮迭代后的估计器的系数 $\alpha$：
$${\alpha }_k=\underset{\alpha }{\mathrm{argmin}}\sum _{i=1}^N\log (1+e^{-2y_i(H_{k-1}(X_i)+\alpha h_k(X_i))})$$

式2-7

  我们先来看下这个回归树估计器 h(x) ，其表达式可以写成下式，其中回归树一共有 J 个叶子结点，$R_j$ 、${\beta }_j$分别代表回归树第 j 个叶子结点包含的训练集合和取值， $I(x)$ 为前面章节中提到过的指示函数：
$$h(x)=\sum _{j=1}^J{\beta }_{j}I(x\in R_j)$$

式2-8

  这时将式 2-8 带入式 2-7 中改写一下，这时就不再是求估计器的系数 alpha，转而直接求 $\gamma$，其中${\gamma }_{k,j}={\alpha }_k\ast {\beta }_{k,j}$：
$${\gamma }_{k,j}=\underset{\gamma }{\mathrm{argmin}}\sum _{X_i\in R_{k,j}}\log (1+e^{-2y_i(H_{k-1}(X_i)+\gamma )})$$

式2-9

  由于式 2-9 中包含了对数指数函数，导致其没有闭式解，这时可以使用二阶泰勒公式对其进行近似处理得到如下结果：
$${\gamma }_{k,j}=\frac{{\sum }_{X_i\in R_{k,j}}{\hat{y}}_{k,i}}{{\sum }_{X_i\in R_{k,j}}|{\hat{y}}_{k,i}|(2-|{\hat{y}}_{k,i}|)}$$

式2-10

  得到 gamma 后更新 H(x) ，然后进行新的迭代。
  这样就得到了二分类的 GBDT 算法实现，具体步骤可以参考第三节的算法步骤中的二分类部分，具体的公式的来由可以参考第四节的原理证明。

多分类

  多分类相对二分类更复杂一些，同样是使用对数函数作为其代价函数，还用到了前面多分类对数几率回归算法中介绍的 Softmax 函数，同时还需对输入的标签值 y 进行 One-Hot 编码⁴ 操作，其代价函数如下：
$$\begin{array}{rlr}Cost(y,H(x))& =\sum _{m=1}^M{y}_m\log p_m(x)& (1)\\ p_m(x)& =\frac{e^{H_m(x)}}{{\sum }_{l=1}^M{e}^{H_l(x)}}& (2)\end{array}$$

式2-11

  同样按照前面模型介绍的计算负梯度的方法，带入代价函数计算出 $\hat{y}$ ：
$$\begin{array}{rlr}{\hat{y}}_{k,m,i}& =-{\left[\frac{\partial Cost(y_i,H(X_i))}{\partial H(X_i)}\right]}_{H(x)=H_{k-1}(x)}& (1)\\ & =y_{m,i}-p_{k-1,m}(X_i)& (2)\end{array}$$

式2-12

  同二分类一样，拟合回归树，同时将其转化为求对应的 $\gamma$，不同的是需要对每一个分类都拟合一个回归树，所以多分类一共需要拟合 K * M 个决策回归树：
$${\gamma }_{k,m,j}=\underset{\gamma }{\mathrm{argmin}}\sum _{i=1}^N\sum _{m=1}^{M}Cost\left(y_{m,i},H_{k-1,m}(X_i)+\sum _{j=1}^J\gamma I(X_i\in R_{k,m,j})\right)$$

式2-13

  同样使用泰勒公式对其进行近似处理得到如下结果：
$${\gamma }_{k,m,j}=\frac{M-1}{M}\frac{{\sum }_{X_i\in R_{k,m,j}}{\hat{y}}_{k,m,i}}{{\sum }_{X_i\in R_{k,m,j}}|{\hat{y}}_{k,m,i}|(1-|{\hat{y}}_{k,m,i}|)}$$

式2-14

  得到 $\gamma$ 后更新对应分类的 H(x) ，然后进行新的迭代。
  这样就得到了多分类的 GBDT 算法实现，具体步骤可以参考第三节的算法步骤中的多分类部分。

三、算法步骤

回归

  假设训练集 T = { $X_i$, $y_i$ }，i = 1，…，N，h(x) 为估计器，估计器的数量为 K。

梯度提升决策树回归算法步骤如下：

初始化 $H_0(x)$，令其等于 y 的平均值 $\bar{y}$
$$H_0(X_i)=\bar{y}$$

遍历估计器的数量 K 次：
  计算第 k 轮的残差 ${\hat{y}}_k$
$${\hat{y}}_{k,i}=y_i-H_{k-1}(X_i)$$

  将第 k 轮 ${\hat{y}}_k$ 当作标签值拟合训练集，得到决策回归树估计器 $h_k(x)$
  更新 $H_k(x)$
$$H_k(X_i)=H_{k-1}(X_i)+h_k(X_i)$$

结束循环

最后的预测策略：

  输入 x ，K 个决策回归树估计器依次预测后相加，然后加上初始值 $H_0$，得到最后的预测结果
$$H(x)=H_0+\sum _{k=1}^K{h}_k(x)$$

二分类

  假设训练集 T = { $X_i$, $y_i$ }，i = 1，…，N，$y_i\in \{-1,+1\}$ ，h(x) 为估计器，估计器的数量为 K。

梯度提升决策树二分类算法步骤如下：

初始化 $H_0(x)$，其中 $\bar{y}$ 为 y 的平均值
$$H_0(X_i)=\frac{1}{2}\log \frac{1+\bar{y}}{1-\bar{y}}$$

遍历估计器的数量 K 次：
  计算第 k 轮的 ${\hat{y}}_k$
$${\hat{y}}_{k,i}=\frac{2y_i}{1+e^{2y_i{H}_{k-1}(X_i)}}$$

  将第 k 轮 ${\hat{y}}_k$ 当作标签值拟合训练集，得到决策回归树估计器 $h_k(x)$，其中 $h_k(x)$ 包含 J 个叶子结点
  计算第 k 轮第 j 个叶子结点的系数 $\gamma$，其中 $R_{kj}$ 代表第 k 轮拟合出的决策回归树估计器 $h_k(x)$ 第 j 个叶子结点包含的训练集合
$${\gamma }_{k,j}=\frac{{\sum }_{X_i\in R_{k,j}}{\hat{y}}_{k,i}}{{\sum }_{X_i\in R_{k,j}}|{\hat{y}}_{k,i}|(2-|{\hat{y}}_{k,i}|)}$$

  更新 $H_k(x)$，其中 $I(x)$ 为前面章节中提到过的指示函数
$$H_k(X_i)=H_{k-1}(X_i)+\sum _{j=1}^J{\gamma }_{k,j}I(X_i\in R_{k,j})$$

结束循环

最后的预测策略：

  输入 x ，K 个决策回归树估计器依次判断所属叶子结点，将叶子结点对应的系数 $\gamma$ 累加，然后加上初始值 $H_0$，得到 H(x)
$$H(x)=H_0+\sum _{k=1}^K\sum _{j=1}^J{\gamma }_{k,j}I(x\in R_{k,j})$$

  分别计算正类和负类的概率
$$\{\begin{array}{rl}{p}_{+}(x)& =\frac{1}{1+e^{-2H(x)}}\\ p_{-}(x)& =\frac{1}{1+e^{2H(x)}}\end{array}$$

  取正类和负类概率中最大的分类，作为最后的分类结果
$$\underset{m}{\mathrm{argmax}}{p}_m(x)(m\in \{+,-\})$$

多分类

  假设训练集 T = { $X_i,y_i$ }，i = 1，…，N，y 的取值有 M 种可能，h(x) 为估计器，估计器的数量为 K。

梯度提升决策树多分类算法步骤如下：

对训练集中的标签值 y 进行 One-Hot 编码
初始化 $H_{0,m}(x)$，其中 m 为第 m 个分类，在原始论文中赋值为 0 ，而 scikit-learn 中的实现为各个分类的先验
$$H_{0,m}(X_i)=\frac{{\sum }_{i=1}^{N}I(y_i=m)}{N}或0$$

遍历估计器的数量 K 次：
  遍历分类的数量 M 次：
    计算第 k - 1 轮第 m 个分类的概率 p(x)
$$p_{k-1,m}(X_i)=\frac{e^{H_{k-1,m}(X_i)}}{{\sum }_{l=1}^M{e}^{H_{k-1,l}(X_i)}}$$

    计算第 k 轮第 m 个分类的 ${\hat{y}}_{k,m}$
$${\hat{y}}_{k,m,i}=y_{m,i}-p_{k-1,m}(X_i)$$

    将第 k 轮第 m 个分类的 ${\hat{y}}_{k,m}$ 当作标签值拟合训练集，得到决策回归树估计器 $h_{k,m}(x)$，其中 $h_{k,m}(x)$ 包含 J 个叶子结点
    计算第 k 轮第 m 个分类第 j 个叶子结点的系数 $\gamma$，其中 $R_{k,m,j}$ 代表第 k 轮第 m 个分类拟合出的决策回归树估计器 $h_{k,m}(x)$ 第 j 个叶子结点包含的训练集合
$${\gamma }_{k,m,j}=\frac{M-1}{M}\frac{{\sum }_{X_i\in R_{k,m,j}}{\hat{y}}_{k,m,i}}{{\sum }_{X_i\in R_{k,m,j}}|{\hat{y}}_{k,m,i}|(1-|{\hat{y}}_{k,m,i}|)}$$

    更新 $H_{k,m}(x)$，其中 $I(x)$ 为前面章节中提到过的指示函数
$$H_{k,m}(X_i)=H_{k-1,m}(X_i)+\sum _{j=1}^J{\gamma }_{k,m,j}I(X_i\in R_{k,m,j})$$

  结束循环
结束循环

最后的预测策略：

  输入 x ，第 m 个分类对应的 K 个决策回归树估计器依次判断所属叶子结点，将叶子结点对应的系数 $\gamma$ 累加，然后加上第 m 个分类的初始值 $H_0$，得到第 m 个分类的 H(x)
$$H_m(x)=H_{0,m}+\sum _{k=1}^K\sum _{j=1}^J{\gamma }_{k,m,j}I(x\in R_{k,m,j})$$

  依次计算每个分类的概率
$$p_m(x)=\frac{e^{H_m(x)}}{{\sum }_{l=1}^M{e}^{H_l(x)}}$$

  取每个分类的概率中最大的分类，作为最后的分类结果
$$\underset{m}{\mathrm{argmax}}{p}_m(x)(m=1,2,\dots ,M)$$

四、原理证明

回归问题初始值

  对于用平方误差作为代价函数的最小二乘回归，其初始值为 y 的均值：
（1）回归问题的代价函数
（2）对代价函数求导数并令其等于零
（3）可以算出其初始值为 y 的均值
$$\begin{array}{rlr}Cost(H(x))& =\sum _{i=1}^N(y_i-H(x){)}^2& (1)\\ \frac{\partial Cost(H(x))}{\partial H(x)}& =2\sum _{i=1}^N(H(x)-y_i)=0& (2)\\ H(x)& =\frac{{\sum }_{i=1}^N{y}_i}{N}=\bar{y}& (3)\end{array}$$

式4-1

  即得证

二分类问题初始值

  对于二分类问题，$y\in \{-1,+1\}$：
（1）$y=+1$ 的个数
（2）$y=-1$ 的个数
（3）两式之和为 N
$$\begin{array}{rlr}{n}_{+}& =\sum _{i=1}^{N}I(y_i=+1)& (1)\\ n_{-}& =\sum _{i=1}^{N}I(y_i=-1)& (2)\\ N& =n_{+}+n_{-}& (3)\end{array}$$

式4-2

（1）y 的平均值的表达式
（2）化简得到
$$\begin{array}{rlr}\bar{y}& =\frac{1\ast n_{+}+(-1)\ast n_{-}}{N}& (1)\\ & =\frac{n_{+}-n_{-}}{N}& (2)\end{array}$$

式4-3

  由式 4-2 中的（3）式和式 4-3 中的（2）式，可以分别求得如下结果：
$$\begin{array}{rlr}{n}_{+}& =\frac{N(1+\bar{y})}{2}& (1)\\ n_{-}& =\frac{N(1-\bar{y})}{2}& (2)\end{array}$$

式4-4

（1）二分类问题的代价函数
（2）对代价函数求导数
（3）将（2）式的结果拆分为两个连加的和
（4）带入式 4-4 的结果，将连加符号去除
（5）化简后令其等于零
（6）最后可以算出其初始值
$$\begin{array}{rlr}Cost(H(x))& =\sum _{i=1}^N\log (1+e^{-2y_{i}H(x)})& (1)\\ \frac{\partial Cost(H(x))}{\partial H(x)}& =-\sum _{i=1}^N\frac{2y_i}{1+e^{2y_{i}H(x)}}& (2)\\ & =-\sum _{y_i=+1}\frac{2y_i}{1+e^{2y_{i}H(x)}}-\sum _{y_i=-1}\frac{2y_i}{1+e^{2y_{i}H(x)}}& (3)\\ & =-\frac{N(1+\bar{y})}{2}\ast \frac{2}{1+e^{2H(x)}}-\frac{N(1-\bar{y})}{2}\ast \frac{-2}{1+e^{-2H(x)}}& (4)\\ & =-\frac{N(1+\bar{y})}{1+e^{2H(x)}}+\frac{N(1-\bar{y})}{1+e^{-2H(x)}}=0& (5)\\ H(x)& =\frac{1}{2}\log \frac{1+\bar{y}}{1-\bar{y}}& (6)\end{array}$$

式4-5

  即得证

二分类问题系数 $\gamma$

  我们先来看下 $\gamma$ 的优化目标函数：
（1）二分类问题的代价函数
（2）式 2-9 得到的 $\gamma$ 的优化目标
（3）对（2）式在 $H_{k-1}(x)$ 处进行二阶泰勒展开近似
（4）可以看到 $H(x)-H_{k-1}(x)$ 等于 $\gamma$
$$\begin{array}{rlr}Cost(H(x))& =\sum _{X_i\in R_{k,j}}\log (1+e^{-2y_{i}H(X_i)})& (1)\\ {\gamma }_{k,j}& =\underset{\gamma }{\mathrm{argmin}}\sum _{X_i\in R_{k,j}}\log (1+e^{-2y_i(H_{k-1}(X_i)+\gamma )})& (2)\\ & =\underset{\gamma }{\mathrm{argmin}}\sum _{X_i\in R_{k,j}}Cost(H_{k-1}(X_i))+Cos{t}^{{}^{\prime }}(H_{k-1}(X_i))(H(X_i)-H_{k-1}(X_i))+\frac{1}{2}Cos{t}^{{}^{\prime \prime }}(H_{k-1}(X_i))(H(X_i)-H_{k-1}(X_i){)}^2& (3)\\ & =\underset{\gamma }{\mathrm{argmin}}\sum _{X_i\in R_{k,j}}Cost(H_{k-1}(X_i))+Cos{t}^{{}^{\prime }}(H_{k-1}(X_i))\gamma +\frac{1}{2}Cos{t}^{{}^{\prime \prime }}(H_{k-1}(X_i)){\gamma }^2& (4)\end{array}$$

式4-6

  对其近似进行求解：
（1）式 4-6 得到的 $\gamma$ 的泰勒展开近似
（2）对函数求导并令其为零
（3）得到 $\gamma$ 的结果
$$\begin{array}{rlr}\varphi (\gamma )& =\sum _{X_i\in R_{k,j}}Cost(H_{k-1}(X_i))+Cos{t}^{{}^{\prime }}(H_{k-1}(X_i))\gamma +\frac{1}{2}Cos{t}^{{}^{\prime \prime }}(H_{k-1}(X_i)){\gamma }^2& (1)\\ \frac{\partial \varphi (\gamma )}{\partial \gamma }& =\sum _{X_i\in R_{k,j}}+Cos{t}^{{}^{\prime }}(H_{k-1}(X_i))+Cos{t}^{{}^{\prime \prime }}(H_{k-1}(X_i))\gamma =0& (2)\\ \gamma & =-\frac{{\sum }_{X_i\in R_{k,j}}^{}Cos{t}^{{}^{\prime }}(H_{k-1}(X_i))}{{\sum }_{X_i\in R_{k,j}}^{}Cos{t}^{{}^{\prime \prime }}(H_{k-1}(X_i))}& (3)\end{array}$$

式4-7

  下面依次求代价函数的一阶导数和二阶导数：
$$\begin{array}{rlr}Cos{t}^{{}^{\prime }}(H_{k-1}(X_i))& =-\frac{2y_i}{1+e^{2y_i{H}_{k-1}(X_i)}}=-\widehat{y_i}& (1)\\ Cos{t}^{{}^{\prime \prime }}(H_{k-1}(X_i))& =\frac{4y_i^2{e}^{2y_i{H}_{k-1}(X_i)}}{(1+e^{2y_i{H}_{k-1}(X_i)}{)}^2}=2\widehat{y_i}{y}_i-{\hat{y}}_i^2& (2)\end{array}$$

式4-8

（1）式 4-7 中得到的 $\gamma$ 的表达式
（2）带入式 4-8 得到
（3）当 $y=+1$ 时，$\hat{y}\in (0,2)$，当 $y=-1$ 时，$\hat{y}\in (-2,0)$，所以 $\hat{y}\ast y=|\hat{y}|$
（4）分母提出 $|\hat{y}|$
$$\begin{array}{rlr}\gamma & =-\frac{{\sum }_{X_i\in R_{k,j}}^{}Cos{t}^{{}^{\prime }}(H_{k-1}(X_i))}{{\sum }_{X_i\in R_{k,j}}^{}Cos{t}^{{}^{\prime \prime }}(H_{k-1}(X_i))}& (1)\\ & =\frac{{\sum }_{X_i\in R_{k,j}}^{}{\hat{y}}_i}{{\sum }_{X_i\in R_{k,j}}^{}(2{\hat{y}}_i{y}_i-{\hat{y}}_i^2)}& (2)\\ & =\frac{{\sum }_{X_i\in R_{k,j}}^{}{\hat{y}}_i}{{\sum }_{X_i\in R_{k,j}}^{}(2|{\hat{y}}_i|-{\hat{y}}_i^2)}& (3)\\ & =\frac{{\sum }_{X_i\in R_{k,j}}{\hat{y}}_i}{{\sum }_{X_i\in R_{k,j}}|{\hat{y}}_i|(2-|{\hat{y}}_i|)}& (4)\end{array}$$

式4-9

  即得证

多分类问题系数 $\gamma$

  多分类问题的系数 $\gamma$ 由于存在多棵树重叠，涉及到黑塞矩阵，无法像二分类一样单独求解，论文中是使用对角近似其黑塞矩阵，直接给出了结果，由于笔者能力有限，如有知道如何推导出结果的读者请留言或私信。

五、正则化

  梯度提升树同样也需要进行正则化操作来防止过拟合的情况，其正则化的方法一般有如下几种方式：

学习速率

  在每次迭代更新 H(x) 时增加一个学习速率 $\eta$ 的超参数，下式中分别展示了学习速率 $\eta$ 在不同问题中的使用方法：
$$\begin{array}{rlr}{H}_k(x)& =H_{k-1}(x)+\eta {\alpha }_k{h}_k(x)& (1)\\ H_k(x)& =H_{k-1}(x)+\eta \sum _{j=1}^J{\gamma }_{k,j}I(x\in R_{k,j})& (2)\\ H_{k,m}(x)& =H_{k-1,m}(x)+\eta \sum _{j=1}^J{\gamma }_{k,m,j}I(x\in R_{k,m,j})& (3)\end{array}$$

式5-1

  其中学习速率 $\eta \in (0,1]$ ，当学习速率 $\eta$ 过小时，需要增加迭代次数才能达到好的学习效果，所以我们需要综合考虑该超参数的使用。在 scikit-learn 中使用 learning_rate 参数来控制。

子采样

  子采样类似于随机梯度下降的方法，每次只取一部分的训练集来学习，可以减小方差，但是同时也会增加偏差。在 scikit-learn 中使用 subsample 参数来控制，同样为大于 0 小于等于 1 的小数。

决策树枝剪

  决策树枝剪同前面在决策树章节中介绍的方法一样，通过对基估计器的控制来达到正则化的目的。在 scikit-learn 中使用决策树相关的参数来控制。

  下面代码实现中只实现了利用学习速率来正则化的操作，其他的方法可以参考 scikit-learn 的源码实现。

六、代码实现

使用 Python 实现梯度提升树回归算法：

import numpy as np
from sklearn.tree import DecisionTreeRegressor

class gbdtr:
    """
    梯度提升树回归算法
    """
    
    def __init__(self, n_estimators = 100, learning_rate = 0.1):
        # 梯度提升树弱学习器数量
        self.n_estimators = n_estimators
        # 学习速率
        self.learning_rate = learning_rate
        
    def fit(self, X, y):
        """
        梯度提升树回归算法拟合
        """
        # 初始化 H0
        self.H0 = np.average(y)
        # 初始化预测值
        H = np.ones(X.shape[0]) * self.H0
        # 估计器数组
        estimators = []
        # 遍历 n_estimators 次
        for k in range(self.n_estimators):
            # 计算残差 y_hat
            y_hat = y - H
            # 初始化决策回归树估计器
            estimator = DecisionTreeRegressor(max_depth = 3)
            # 用 y_hat 拟合训练集
            estimator.fit(X, y_hat)
            # 使用回归树的预测值
            y_predict = estimator.predict(X)
            # 更新预测值
            H += self.learning_rate * y_predict
            estimators.append(estimator)
        self.estimators = np.array(estimators)
        
    def predict(self, X):
        """
        梯度提升树回归算法预测
        """
        # 初始化预测值
        H = np.ones(X.shape[0]) * self.H0
        # 遍历估计器
        for k in range(self.n_estimators):
            estimator = self.estimators[k]
            y_predict = estimator.predict(X)
            # 计算预测值
            H += self.learning_rate * y_predict
        return H

使用 Python 实现梯度提升树二分类算法：

import numpy as np
from sklearn.tree import DecisionTreeRegressor

class gbdtc:
    """
    梯度提升树二分类算法
    """
    
    def __init__(self, n_estimators = 100, learning_rate = 0.1):
        # 梯度提升树弱学习器数量
        self.n_estimators = n_estimators
        # 学习速率
        self.learning_rate = learning_rate
        
    def fit(self, X, y):
        """
        梯度提升树二分类算法拟合
        """
        # 标签类
        self.y_classes = np.unique(y)
        # 标签类数量
        self.n_classes = len(self.y_classes)
        # 标签的平均值
        y_avg = np.average(y)
        # 初始化H0
        self.H0 = np.log((1 + y_avg) / (1 - y_avg)) / 2
        # 初始化预测值
        H = np.ones(X.shape[0]) * self.H0
        # 估计器数组
        estimators = []
        # 叶子结点取值数组
        gammas = []
        for k in range(self.n_estimators):
            # 计算 y_hat
            y_hat = 2 * np.multiply(y, 1 / (1 + np.exp(2 * np.multiply(y, H))))
            # 初始化决策回归树估计器
            estimator = DecisionTreeRegressor(max_depth = 3, criterion="friedman_mse")
            # 将 y_hat 当作标签值拟合训练集
            estimator.fit(X, y_hat)
            # 计算训练集在当前决策回归树的叶子结点
            leaf_ids = estimator.apply(X)
            # 每个叶子结点下包含的训练数据序号
            node_ids_dict = self.get_leaf_nodes(leaf_ids)
            # 叶子结点取值字典表
            gamma_dict = {}
            # 计算叶子结点取值
            for leaf_id, node_ids in node_ids_dict.items():
                # 当前叶子结点包含的 y_hat
                y_hat_sub = y_hat[node_ids]
                y_hat_sub_abs = np.abs(y_hat_sub)
                # 计算叶子结点取值
                gamma = np.sum(y_hat_sub) / np.sum(np.multiply(y_hat_sub_abs, 2 - y_hat_sub_abs))
                gamma_dict[leaf_id] = gamma
                # 更新预测值
                H[node_ids] += self.learning_rate * gamma
            estimators.append(estimator)
            gammas.append(gamma_dict)
        self.estimators = estimators
        self.gammas = gammas
        
    def predict(self, X):
        """
        梯度提升树二分类算法预测
        """
        # 初始化预测值
        H = np.ones(X.shape[0]) * self.H0
        # 遍历估计器
        for k in range(self.n_estimators):
            estimator = self.estimators[k]
            # 计算在当前决策回归树的叶子结点
            leaf_ids = estimator.apply(X)
            # 每个叶子结点下包含的数据序号
            node_ids_dict = self.get_leaf_nodes(leaf_ids)
            # 叶子结点取值字典表
            gamma_dict = self.gammas[k]
            # 计算预测值
            for leaf_id, node_ids in node_ids_dict.items():
                gamma = gamma_dict[leaf_id]
                H[node_ids] += self.learning_rate * gamma
        # 计算概率
        probs = np.zeros((X.shape[0], self.n_classes))
        probs[:, 0] = 1 / (1 + np.exp(2 * H))
        probs[:, 1] = 1 / (1 + np.exp(-2 * H))
        return self.y_classes.take(np.argmax(probs, axis=1), axis = 0)
    
    def get_leaf_nodes(self, leaf_ids):
        """
        每个叶子结点下包含的数据序号
        """
        node_ids_dict = {}
        for j in range(len(leaf_ids)):
            leaf_id = leaf_ids[j]
            node_ids = node_ids_dict.setdefault(leaf_id, [])
            node_ids.append(j)
        return node_ids_dict

使用 Python 实现梯度提升树多分类算法：

import numpy as np
from sklearn.tree import DecisionTreeRegressor

class gbdtmc:
    """
    梯度提升树多分类算法
    """
    
    def __init__(self, n_estimators = 100, learning_rate = 0.1):
        # 梯度提升树弱学习器数量
        self.n_estimators = n_estimators
        # 学习速率
        self.learning_rate = learning_rate
        
    def fit(self, X, y):
        """
        梯度提升树多分类算法拟合
        """
        # 标签类，对应标签的数量
        self.y_classes, y_counts = np.unique(y, return_counts = True)
        # 标签类数量
        self.n_classes = len(self.y_classes)
        # 对标签进行One-Hot编码
        y_onehot = np.zeros((y.size, y.max() + 1))
        y_onehot[np.arange(y.size), y] = 1
        # 初始化 H0
        self.H0 = y_counts / X.shape[0]
        # 初始化预测值
        H = np.ones((X.shape[0], 1)).dot(self.H0.reshape(1, -1))
        # 估计器数组
        estimators = []
        # 叶子结点取值数组
        gammas = []
        # 遍历 n_estimators 次
        for k in range(self.n_estimators):
            H_exp = np.exp(H)
            H_exp_sum = np.sum(H_exp, axis = 1)
            # 估计器
            sub_estimators = []
            # 叶子结点取值
            sub_gammas = []
            # 遍历 n_classes 次
            for m in range(self.n_classes):
                p_m = H_exp[:, m] / H_exp_sum
                # 计算第 m 个 y_hat
                y_hat_m = y_onehot[:, m] - p_m
                # 初始化决策回归树估计器
                estimator = DecisionTreeRegressor(max_depth = 3, criterion="friedman_mse")
                # 将第 m 个 y_hat 当作标签值拟合训练集
                estimator.fit(X, y_hat_m)
                # 计算训练集在当前决策回归树的叶子结点
                leaf_ids = estimator.apply(X)
                # 每个叶子结点下包含的训练数据序号
                node_ids_dict = self.get_leaf_nodes(leaf_ids)
                # 叶子结点取值字典表
                gamma_dict = {}
                # 计算叶子结点取值
                for leaf_id, node_ids in node_ids_dict.items():
                    # 当前叶子结点包含的 y_hat
                    y_hat_sub = y_hat_m[node_ids]
                    y_hat_sub_abs = np.abs(y_hat_sub)
                    # 计算叶子结点取值
                    gamma = np.sum(y_hat_sub) / np.sum(np.multiply(y_hat_sub_abs, 1 - y_hat_sub_abs)) * (self.n_classes - 1) / self.n_classes
                    gamma_dict[leaf_id] = gamma
                    # 更新预测值
                    H[node_ids, m] += self.learning_rate * gamma
                sub_estimators.append(estimator)
                sub_gammas.append(gamma_dict)
            estimators.append(sub_estimators)
            gammas.append(sub_gammas)
        self.estimators = estimators
        self.gammas = gammas
        
    def predict(self, X):
        """
        梯度提升树多分类算法预测
        """
        # 初始化预测值
        H = np.ones((X.shape[0], 1)).dot(self.H0.reshape(1, -1))
        # 遍历估计器
        for k in range(self.n_estimators):
            sub_estimators = self.estimators[k]
            sub_gammas = self.gammas[k]
            # 遍历分类数
            for m in range(self.n_classes):
                estimator = sub_estimators[m]
                # 计算在当前决策回归树的叶子结点
                leaf_ids = estimator.apply(X)
                # 每个叶子结点下包含的训练数据序号
                node_ids_dict = self.get_leaf_nodes(leaf_ids)
                # 叶子结点取值字典表
                gamma_dict = sub_gammas[m]
                # 计算预测值
                for leaf_id, node_ids in node_ids_dict.items():
                    gamma = gamma_dict[leaf_id]
                    H[node_ids, m] += self.learning_rate * gamma
        H_exp = np.exp(H)
        H_exp_sum = np.sum(H_exp, axis = 1)
        # 计算概率
        probs = np.zeros((X.shape[0], self.n_classes))
        for m in range(self.n_classes):
            probs[:, m] = H_exp[:, m] / H_exp_sum
        return self.y_classes.take(np.argmax(probs, axis=1), axis = 0)
    
    def get_leaf_nodes(self, leaf_ids):
        """
        每个叶子结点下包含的数据序号
        """
        node_ids_dict = {}
        for j in range(len(leaf_ids)):
            leaf_id = leaf_ids[j]
            node_ids = node_ids_dict.setdefault(leaf_id, [])
            node_ids.append(j)
        return node_ids_dict

七、第三方库实现

scikit-learn⁵ 实现：

from sklearn.ensemble import GradientBoostingClassifier

# 梯度提升树分类器
clf = GradientBoostingClassifier(n_estimators = 100)
# 拟合数据集
clf = clf.fit(X, y)

scikit-learn⁶ 实现：

from sklearn.ensemble import GradientBoostingRegressor

# 梯度提升树回归器
reg = GradientBoostingRegressor(n_estimators = 100, max_depth = 3, random_state = 0, loss = 'ls')
# 拟合数据集
reg = reg.fit(X, y)

八、示例演示

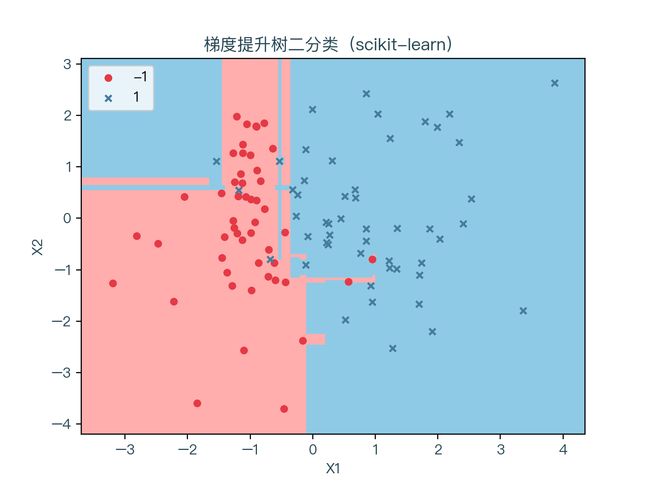
  下面三张图片分别展示了使用梯度提升算法进行二分类，多分类与回归的结果

图8-1

图8-2

图8-3

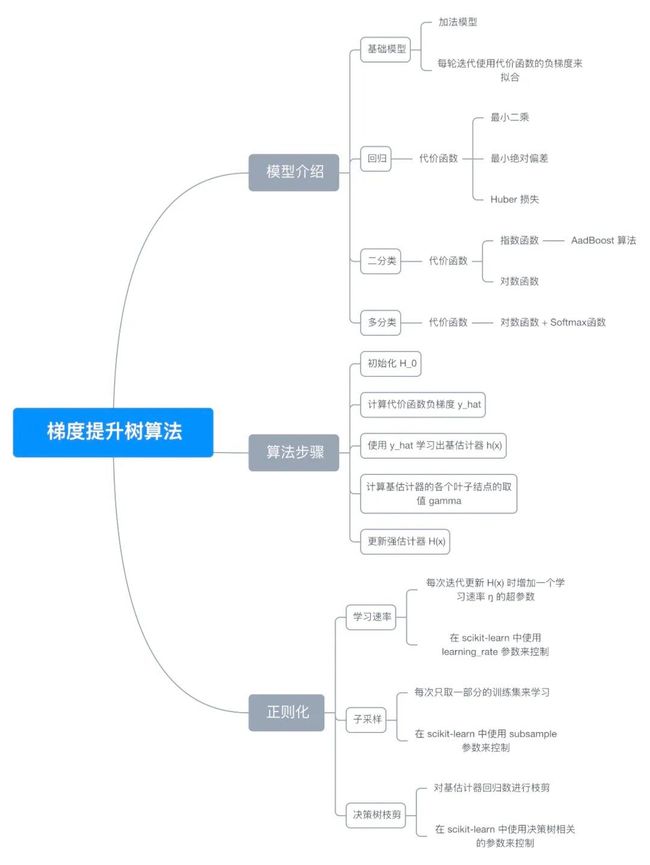
九、思维导图

图9-1

十、参考文献

1. https://en.wikipedia.org/wiki/Gradient_boosting
2. https://www.cse.cuhk.edu.hk/irwin.king/_media/presentations/2001_greedy_function_approximation_a_gradient_boosting_machine.pdf
3. https://en.wikipedia.org/wiki/Huber_loss
4. https://en.wikipedia.org/wiki/One-hot
5. https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html
6. https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html

完整演示请点击这里

注：本文力求准确并通俗易懂，但由于笔者也是初学者，水平有限，如文中存在错误或遗漏之处，恳请读者通过留言的方式批评指正

本文首发于——AI导图，欢迎关注