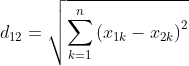【机器学习】KNN算法实现

目录

1.概述

1.1实例距离计算

2.knn实现图像分类

2.1数据集

2.2数据集预处理 

2.3划分数据集

2.4定义knn分类器

2.5测试结果

2.6结果分析

3.优化算法

3.1计算特征向量

3.2knn加权

---

1.概述

knn即k近邻算法，给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例， 这K个实例的多数属于某个类，就把该输入实例分类到这个类中。

如下图所示，

k取1时，最靠近中心的一个实例为一个圆形数据，即把实例归为圆形数据类。

k取3时，最靠近中心的三个实例为两个圆形数据和一个方形数据，即把实例归为圆形数据类。

k取5时，最靠近中心的五个实例为两个圆形数据和三个方形数据，即把实例归为方形数据类。

1.1实例距离计算

在寻找最邻近的实例时，需要计算实例之间的距离作为判断依据，常用的距离公式有欧式距离，曼哈顿距离，汉明距离，余弦距离等，以欧式距离为例：

二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离：

三维空间两点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离:

两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离：

2.knn实现图像分类

2.1数据集

本次数据集收集自JMU的宿舍门，楼梯，灭火箱三种类别的图像

 

 

2.2数据集预处理 

分别从三个目标类别文件夹中读取图像数据集，将图像数据归一化后以numpy数据类型存储

class DataStructure:
    def __init__(self, width, height):
        self.width = width
        self.height = height
    
    def load(self, paths):
        #定义存储图像数据和标签的list变量
        data , labels = [],[]

        for (i, path) in enumerate(os.listdir(paths)):
            imgdir = os.path.join(paths,path)

            for imgname in os.listdir(imgdir):
                #读取rbg三通道图像
                img = cv2.imread(os.path.join(imgdir,imgname),1)

                #将图像归一化数据为0-1之间
                img = (img - np.min(img)) / (np.max(img) - np.min(img))

                #将图像缩放到同一尺度大小
                img = cv2.resize(img,(self.width,self.height))

                data.append(img)
                labels.append(path)
        
        return (np.array(data), np.array(labels))

2.3划分数据集

随机打乱数据集并按设定的比例将数据集分为训练集和测试集

def randdata(dataset):

    train_data,train_label =[],[]

    # 生成数据集索引序列
    index = list(range(0,len(dataset[0])))

    # 打乱索引序列
    random.shuffle(index)

    # 利用打乱的索引序列重新排序数据集
    for i in index:
        train_data.append(dataset[0][i])
        train_label.append(dataset[1][i])
    
    return (train_data,train_label)

def SplitDataset(dataset, n_splits):
    # 打乱数据集
    dataset = randdata(dataset)

    n = len(dataset[0])

    # 按比例划分数据集
    train_x = dataset[0][:int(n*n_splits)]
    test_x = dataset[0][int(n*n_splits):]
    train_y = dataset[1][:int(n*n_splits)]
    test_y = dataset[1][int(n*n_splits):]

    return ((train_x,train_y),(test_x,test_y))

2.4定义knn分类器

class knn:
    def __init__(self, k):
        # 初始化k值
        self.k = k

    def euler_distance(self, x1, x2):
        # 将三通道图像数据展平为一维
        x1 = np.asarray(x1).flatten()
        x2 = np.asarray(x2).flatten()

        # 按欧拉公式计算两个实例向量的距离
        d1 = np . sqrt ( np . sum ( np . square ( x1 - x2 ) ) )

        return d1

    def fit(self,train_data,test_data):

        train_x,train_y = train_data[0],train_data[1]
        test_x,test_y = test_data[0],test_data[1]


        dis = []
        pre_labe = []
        
        # 循环计算测试数据集和每个训练数据的距离
        for (i,X) in enumerate(test_x):
            labels = []

            for(j,x) in enumerate(train_x):
                #存储实例间的距离和对应的索引
                dis.append([i,j,self.euler_distance(X,x)])
                distance = np.array(dis)   
                #将存储的距离和对应的索引按照距离进行从小到大的排序   
                distance = distance[np.lexsort(distance.T)]

            
            # 添加最近的k个训练实例
            for l in range(self.k):

                labels.append(train_y[int(list(distance[l])[1])])

            # 统计最近k个实例中每个标签对应的数量
            result=Counter(labels)
            # 按标签数量从大到小进行排序
            re = sorted(result.items(), key=lambda item:item[1], reverse = True)


            # 添加数量最多的标签
            pre_labe.append(re[0][0])
        
        return pre_labe

2.5测试结果

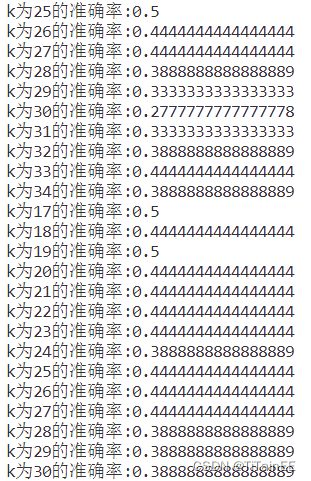
测试多个k值的结果，输出每次k值的测试精度，并且绘制成曲线图进行结果分析

 

def accuracy(pred, test_y):
    count = 0
    for i in range(len(pred)):
        if(test_y[i] == pred[i]):
            count += 1
    acc = count / len(test_y)
    return acc


if __name__ == "__main__":
    # 设置路径
    paths = "./datasets"
    # 实例化类，并设置resize大小为320*240
    imgdata = DataStructure(320,240)
    # 加载，划分数据集
    traindata,testdata = SplitDataset(imgdata.load(paths),0.70)

    accuracy_all = []

    # 测试多个k值的结果并绘制曲线图
    for i in range(1,len(traindata[0])):

        
        model = knn(i)

        pre = model.fit(traindata,testdata)

        acc = accuracy(pre,testdata[1])

        accuracy_all.append(acc)
        print("k为{i}的准确率:{acc}".format(i=i,acc=acc))
    print(testdata[1])
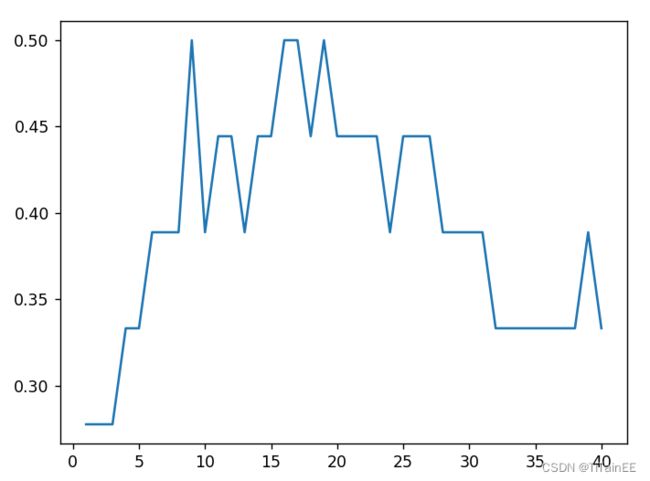
    plt.plot(range(1,len(traindata[0])),accuracy_all)
    plt.show()

2.6结果分析

选取的是图像数据集，图像中的噪声和背景会计算实例距离造成误差影响，从曲线图中可以看到，当K 为0-10 时，受图像质量差异的影响测试精度较低，当K 为10-30时，样本数量比较多，图像间像素强度相近的更容易被统计，当K 大于30时，精确度趋近于百分之33，等k趋近训练样本数时，所有的测试实例会被分为数量最多的一个类别，由于数据集中的三种样本数量相等，若随机打乱的测试集中三种样本依旧均匀分布，则最终的测试结果中只能预测成功三分之一的样本数，精度趋近百分之33。

 

3.优化算法

3.1计算特征向量

在本次实验中，采用图像作为数据集，则会引入噪声，背景杂乱，像素强度差异小等影响因素，导致实验结果不理想，可以以图像特征进行距离计算以提高精度。

HOG特征

方向梯度直方图特征，它通过计算和统计图像局部区域的梯度方向直方图来构成特征。计算图像每个像素的梯度，包括大小和方向，捕获目标轮廓信息，将图像划分成小cells并统计其梯度直方图，每几个cell组成一个block，组合block内所有的梯度直方图得到块特征，最后将图像内的所有block特征组合起来得到图像的HOG特征向量

from skimage.feature import hog

_, hog_image = hog(image,
                    orientations=8,
                    pixels_per_cell=(16, 16),
                    cells_per_block=(1, 1),
                    visualize=True,
                    multichannel=False) 

 

 

3.2knn加权

对于数据集不均衡的情况下，预测结果会偏向样本数量多的情况，通过给实例的距离加权可以优化误差，将距离该实例中心近的样本权值增加，距离该实例中心远的样本权值减小。

反函数

返回的权重为距离的倒数，避免过于接近的样本权重过大，在计算时增加一个常量const

def invweight(dist, num=1., const=0.1):
    return num / (dist + const)

高斯函数

该函数在距离为 0 的时候，所得的权重为 1， 并且权重会随着距离的增加而减少

def gaussian(dist, a=1, b=0, c=0.3):
    return a * math.e ** (-(dist - b) ** 2 / (2 * c ** 2))

加权后的距离计算

weight = invweight(self.euler_distance(X,x))
dis.append([i,j,self.euler_distance(X,x)+ weight*1])