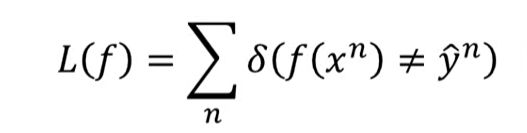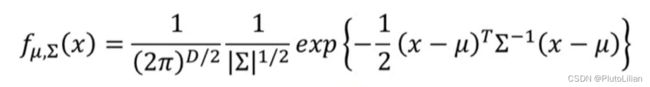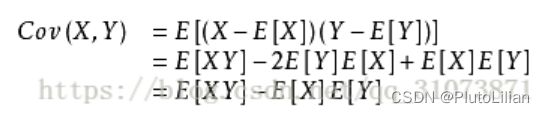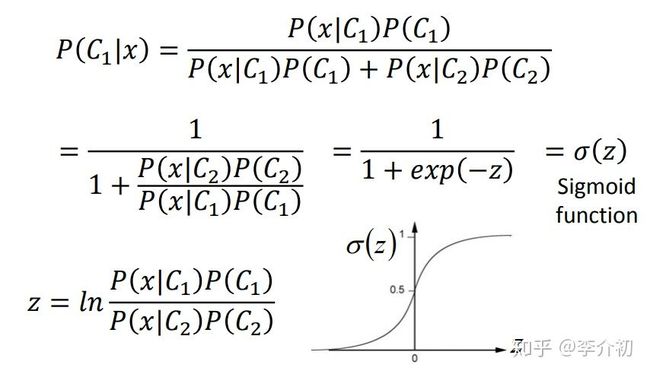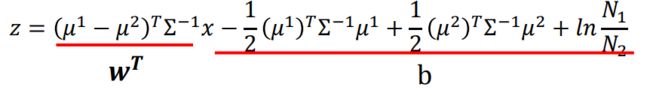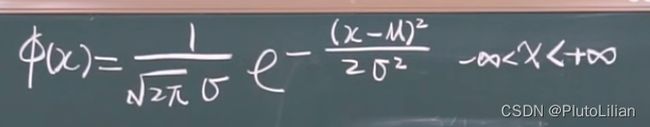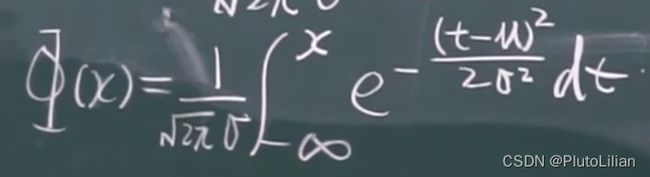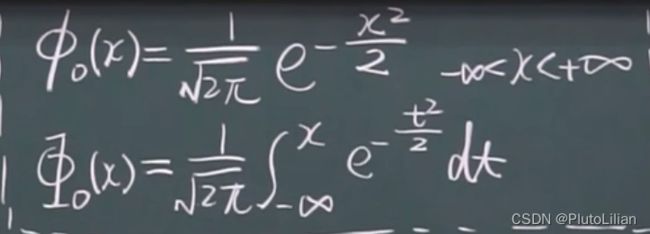机器学习笔记
Classification分类问题
与regression的区别在于，regression的输出可以是任意实数，其函数图是连续的，而分类问题的输出是离散的。
输入数值化
如何用数值描述一个样本？
为什么不能用regression做分类问题呢？
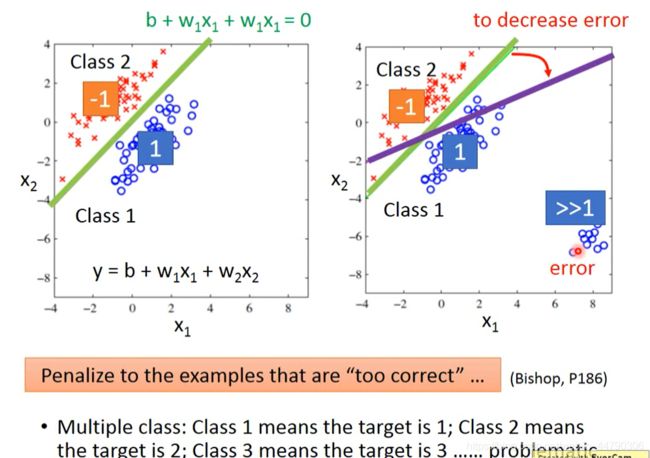
比如我们先用regression得到输出数值，然后判断，大于某个数让他输出class1，小于某个数让他输出class2。
但这样做会有一个问题：因为regression为使loss最小，当有极端值时，曲线会受极端值影响从而像极端值靠近。
也就是说regression会惩罚太正确的样本，得到不好的function。
Ideal alternative
我们重新定义loss函数
期中f(x)输出是其判定的类别， yhat是其真实类别对应的数值。那么这个L就是表示判断失误的次数
但此L无法微分，因此无法用gradient descent做优化，那应该怎么做呢？
Solution1:Generative model(生成式模型）
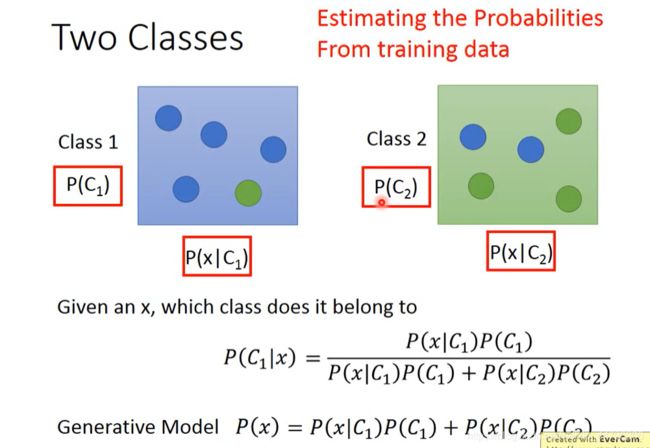
生成式模型先假设概率分布的模型（如高斯分布、伯努利分布、泊松分布），然后用相应的概率公式计算x所属于的类型p(C1∣x)。这里是x属于C1的概率，是间接得到的
每一个class有一个自己的概率分布模型，可以用相应模型的公式算出P（x|C)，再在所有样本集中算出P（C）即可由贝叶斯公式算出。
下面说说具体如何计算P（x|C1)
当拿到一个新的x，显然不能用C1中x的个数除以C1中所有样本个数，因为x暂时还并不属于C1，这样计算得到的只会是0.因此我们需要将每个样本的feature集看成一个向量，然后根据空间中概率分布可得到这个向量属于这类的概率。
以高斯分布为例
如何找到空间中高斯分布的函数呢？（先以两个feature也就是二维空间为例）
已知高斯函数是输入一个样本的特征向量x，输出一个从该类型中sample出x的概率。那么真正要调整的参数是：均值μ和协方差Σ
其中μ决定了概率分布图的最高点出现的位置， Σ决定了概率分布的聚散情况。
补充：协方差相当于多个输入的方差，公式为：
那么如何找到这个μ和Σ呢？
极大似然法
实际上，任意一个高斯分布都有一定可能性sample出已知样本点，但明显概率是不同的，我们要找到就是sample出已知样本概率最大的模型。此时我们需要重新定义一下Loss function，把它定义成如上，也就是sample出每一个已知样本点的概率之积，这就是极大似然函数。
以上是正向思考的结果，那么我们反向考虑如何得到最优的参数，即将极大似然函数求偏导，进行gradient descent
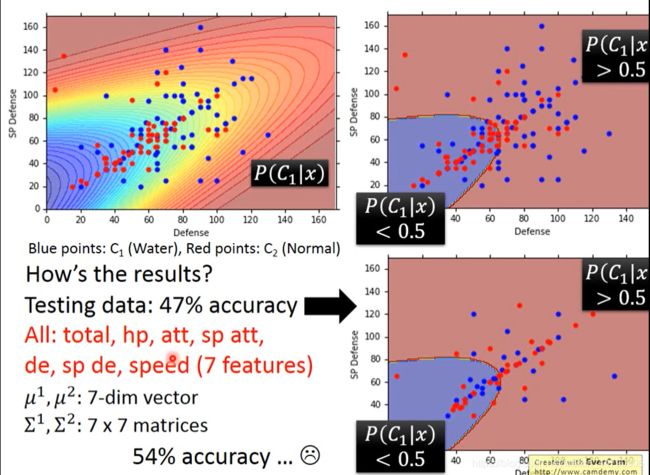
如图为已知公式。现在就有了P（C1），P（x|C1），P（C2），P（x|C2）这四个值，可以开始真的分类了。
那么最后得到的模型究竟好不好呢？
由图，在测试集上表现并不尽如人意。
Midifying model
由于convenience本身就是一个矩阵，其大小与feature input的平方成正比，那么当feature较多时，容易出现太多参数而overfitting的现象。
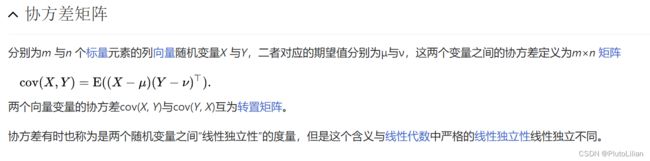
协方差
公式：
用途：在機率論與統計學中用於衡量两个随机变量的联合变化程度。
（若变量X的较大值主要与另一个变量Y的较大值相对应，而两者的较小值也相对应，则可稱兩變數倾向于表现出相似的行为，协方差为正。在相反的情况下，当一个变量的较大值主要对应于另一个变量的较小值时，则两变量倾向于表现出相反的行为，协方差为负。即共變異數之正負號顯示著變數的相关性。）
为解决 这个问题，我们可以让两个类的模型共用一个协方差矩阵，以减少参数。
这里写的μ1μ2is the same 意思是这两个μ仍然和刚才的计算方法一样，不做改变。
而共同的Σ变为原来的两个Σ的加权平均值。
此时极大似然函数变成属于一类的样本在一模型下的概率之积乘上属于二类的在二模型下的概率之积，也就是每个样本来都判断对的概率。
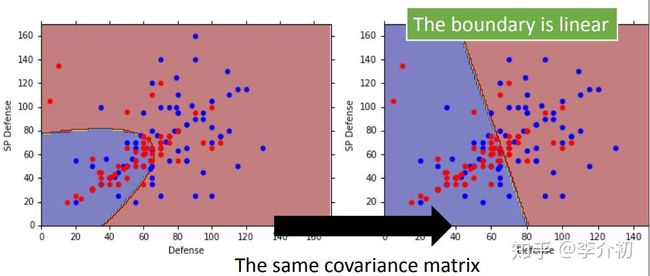
如图可以发现，共用协方差后，边界从原来的非线性变为现在的线性，且判断准确率提高不少。
为什么共用协方差就能让边界变为线性呢?
由下图我们会发现，x属于C1的概率函数其实是一个以z为输入的sigmoid函数
再经过对z表达式的一系列代换，其中sigma统一（数学细节不做深入研究），得到上图所示结构，此时b为scalar，w为矩阵，正好是一个线性回归的模型
判别式和生成式
判别式是通过学习数据学习一个模型，这个模型能够把几种类型分隔开。当遇到新数据时，通过该模型的划分来判断是哪个类型
生成式是对每种类型就它的输入特征构建一个模型，每种类型的模型互不干扰，都可以通过输入新的特征向量得到该数据属于该类型的几率，最后比较谁的几率更大即为该类型。
判别式通常用逻辑回归方法：也就是先拟定参数，，然后用Maximum liklyhood得到最优模型，即为类型的分割线。
生成式通常用高斯分布方法
两者的比较（这里不太懂）
通常判别式比生成式的效果更好。因为生成式会有一个类型的预判，比如高斯或伯努利。生成式会假设概率分布，所以受样本数量影响较小，而判别式会随着样本数量增多而越来越准确。
Multi-class classification
正向思考：我们已知了最优的参数值w,b，可分别算出z123，为拉开大小差距，分别对z求exponential，此时的值为负无穷到正无穷的任意数，再如图求出y123，y为零到一之间的数，且y的和为1，因此y就是对应类型的概率值
知识补充：高斯分布（正态分布）
1，对密度函数求积分为1
2，分布函数
3,性质
1）图像以x=u为对称轴，此时取到最大值
2） 以x轴为渐近线
3）若σ不变，让μ变化，实际上是将图像左右平移
若μ固定，σ变化，σ变小——最高点朝上移动；σ变大——最高点朝下移动（积分仍为1）
4）标准正态分布：μ=0，σ=1，此时
标准正态分布的性质：
4，正态分布的应用：查表
先把一般正态分布化成标准正态分布，然后再查表
5，如何将一般正态分布化成标准正态分布
标准正态分布的输入为（x-μ）/σ
反向思考：未知最优的参数，但肯定有w,b使y最接近y的真实值。则可以设计loss function。
下面我们来总结一下分类算法的步骤
1，定义模型集合并算出样本x属于某一类的概率表达式
2，定义loss function以评价好坏
通常用极大似然函数来评价
3，调整参数知道最好