pytorch geometric教程一: 消息传递源码详解(MESSAGE PASSING)+实例
pytorch geometric教程一: 消息传递源码详解(MESSAGE PASSING)+实例
- pytorch geometric教程一:消息传递源码(MESSAGE PASSING)+实例
-
- 卷积原理回顾
- MessagePassing基类
-
- MessagePassing初始化
- MessagePassing.propagate(edge_index, size=None, **kwargs)
- MessagePassing.message(...)
- MessagePassing.aggregate(inputs, index, ...)
- MessagePassing.update(aggr_out, ...)
- MessagePassing.message_and_aggregate(adj_t, ...)
- 实例
pytorch geometric教程一:消息传递源码(MESSAGE PASSING)+实例
卷积原理回顾
图卷积中最关键的一步就是如何实现消息传递与跟新,通常被称为邻域聚合或者消息传递(neighborhood aggregation or message passing)。图卷积的过程通常可以用以下公式归纳:
x i ( k ) = γ ( k ) ( x i ( k − 1 ) , □ j ∈ N ( i ) ϕ ( k ) ( x i ( k − 1 ) , x j ( k − 1 ) , e j , i ) ) \mathbf{x}_i^{(k)} = \gamma^{(k)} \left( \mathbf{x}_i^{(k-1)}, \square_{j \in \mathcal{N}(i)} \, \phi^{(k)}\left(\mathbf{x}_i^{(k-1)}, \mathbf{x}_j^{(k-1)},\mathbf{e}_{j,i}\right) \right) xi(k)=γ(k)(xi(k−1),□j∈N(i)ϕ(k)(xi(k−1),xj(k−1),ej,i))
其中 x i ( k − 1 ) ∈ R F \mathbf{x}^{(k-1)}_i \in \mathbb{R}^F xi(k−1)∈RF是节点 i i i在第 ( k − 1 ) (k-1) (k−1)层的特征, e j , i ∈ R D \mathbf{e}_{j,i} \in \mathbb{R}^D ej,i∈RD 是节点 j j j到节点 i i i的边特征。边特征不是必须存在的。
上述公式可以拆解为以下三步:
1,消息message
我们需要一个函数来定义每个邻居节点传递给中心节点的消息,也就是上式中的 ϕ ( k ) ( x i ( k − 1 ) , x j ( k − 1 ) , e j , i ) \color{maroon}\bm{\phi^{(k)}\left(\mathbf{x}_i^{(k-1)}, \mathbf{x}_j^{(k-1)},\mathbf{e}_{j,i}\right)} ϕ(k)(xi(k−1),xj(k−1),ej,i)。 ϕ ( k ) \phi^{(k)} ϕ(k)是有关中心节点特征 x i ( k − 1 ) \mathbf{x}_i^{(k-1)} xi(k−1),邻居节点特征 x j ( k − 1 ) \mathbf{x}_j^{(k-1)} xj(k−1),和边 e j , i \mathbf{e}_{j,i} ej,i的可微函数。
2,聚合aggregate
得到每个邻居传递给中心节点的消息后,我们需要用一种可微且置换不变( permutation invariant)的函数来聚合邻域消息。要求置换不变是因为邻居之间是无序的,所以聚合结果不应该随着邻居排序而变化。这一步对应上式中的 □ j ∈ N ( i ) \color{maroon}\bm{\square_{j \in \mathcal{N}(i)}} □j∈N(i)。
3,跟新update
完成邻域消息聚合后,只剩下最后一步,就是结合得到的邻域消息的聚合结果与节点自身的特征,输出这一层最终的embedding。这个对应上式中的 γ ( k ) \color{maroon}\bm{\gamma^{(k)}} γ(k)。
接下来我们就看看pytorch geometric是如何实现这三步的。
MessagePassing基类
pytorch geometric提供了一个MessagePassing基类,它已经通过MessagePassing.propagate()实现了以上三步对应的计算过程。我们只需定义一个继承了MessagePassing基类的class,然后根据具体的图算法来跟新函数 ϕ \phi ϕmessage(), 邻域聚合方式aggr="add", aggr="mean" or aggr="max",以及函数 γ \gamma γupdate(),并在自定义的图算法卷积层中的forward函数里面调用progagate函数就好了。大致流程如下,下面我们分步解释代码。
import torch
from torch_geometric.nn import MessagePassing
class NameConv(MessagePassing):
def __init__(self, in_channels, out_channels, **kwargs):
kwargs.setdefault('aggr', 'add')
super(NameConv, self).__init__(**kwargs)
...
def forward(self, x, edge_index):
...
return self.propagate(edge_index, **kwargs)
def message(self, **kwargs):
...
MessagePassing初始化
def __init__(self, aggr: Optional[str] = "add",
flow: str = "source_to_target", node_dim: int = -2,
decomposed_layers: int = 1):
aggr:邻域聚合方式,默认add,还可以是mean, max。flow:消息传递方向,默认从source_to_target,也可以设置为target_to_source,不过source_to_target是最通常的传递机制,也就是从节点 j j j传递消息到节点 i i i。node_dim:定义沿着哪个维度进行消息传递,默认-2,因为-1是特征维度。
MessagePassing.propagate(edge_index, size=None, **kwargs)
这里实现消息传递,也就是以上图卷积中三个步骤的地方。progagate会依次调用message, aggregate,update方法。如果edge_index是SparseTensor,会优先message_and_aggregate来代替message和aggregate。下面依次解释一下progagate中的三个参数以及对应的细节。
edge_index:
edge_index提供了给消息如何传递提供了信息。它有两种形式:Tensor和SparseTensor。Tensor形式下的edge_index的shape是(2, N)。SparseTensor则可以理解为稀疏矩阵的形式存储边信息。size
当size为None的时候,默认邻接矩阵是方形[N, N]。如果是异构图,比如bipartite图时,图中的两类点的特征和index是相互独立的。通过传入size=(N, M),x=(x_N, x_M)时,propagate可以处理这种情况。- kwargs
图卷积计算过程的额外所需的信息,都可以通过kwargs传入。
MessagePassing.message(…)
这个方法对应公式中的函数 ϕ \phi ϕ,在flow="source_to_target"的设置下,计算了邻居节点 j j j到中心节点 i i i的消息。传给propagate()所有参数都可以传递给message(),而且传递给propagate()的tensors可以通过加上_i或_j的后缀来mapping到对应的节点。
比如以下代码,x_j代表了每个邻居的特征,它是通过edge_index中邻居节点的index,去索引对应位置的x,则得到x_j。
def message(self, x_j: Tensor) -> Tensor:
return x_j
当edge_index的shape是(2, N_edges),x的shape是(N_nodes, N_features),则得到的x_j的shape是(N_edges, N_features) (敲黑板,理解这点很重要,因为重要,我下面特地举个例子)。
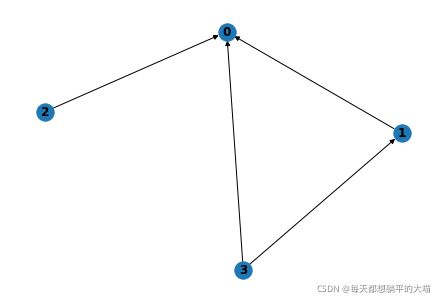
假如我们有以下一张有向图,那么edge_index是这样的: tensor([[1, 2, 3, 3], [0, 0, 0, 1]]),因为有四条有向边,edge_index的shape是(2, 4)。其中邻居节点j的index是edge_index的第一个元素[1, 2, 3, 3]。
另外我们有以下x:
x = tensor([[0, 1],
[2, 3],
[4, 5],
[6, 7]])
根据节点j的index [1, 2, 3, 3],去索引x对应的位置,则得到
# x_j = x[index(j)]
x[[1,2,3,3]] = tensor([[2, 3],
[4, 5],
[6, 7],
[6, 7]])
MessagePassing.aggregate(inputs, index, …)
这个方法实现了邻域的聚合,pytorch geometric通过scatter共实现了三种方式mean, add, max。一般来说,比较通用的图算法,GCN, GraphSAGE, GAT都不需要自己再额外定义aggregate方法。
MessagePassing.update(aggr_out, …)
这个方法对应公式中的函数 γ \gamma γ。之前传入propagate的参数也都传入update。对应每个中心节点 i i i,根据aggregate的邻域结果,以及在传入propagate的参数中选择所需信息,跟新节点 i i i的embedding。
MessagePassing.message_and_aggregate(adj_t, …)
能矩阵计算就矩阵计算!这是提高计算效率,节省计算资源很重要的一点,在图卷积中也同意适用。前面提到pytorch geometric中的边信息有Tensor和SparseTensor两种形式。当边是以SparseTensor,也就是我们通常意义上理解的稀疏矩阵的形式存储的时候,会写成adj_t。(为什么后面加个t,写成转置的形式,请参考我另外一篇博文pytorch geometric中为何要将稀疏邻接矩阵写成转置的形式adj_t)。
SparseTensor提供了矩阵存储形式,message_and_aggregate则提供了邻域聚合的矩阵计算方式(不是所有的图卷积都可以用矩阵计算)。当边是以SparseTensor存储的时候,propagate会优先去查找是否实现了message_and_aggregate如果已经实现了,就会调用message_and_aggregate来代替message和aggregate。如果没有实现,propagate需要将边信息转换为Tensor,然后再调用message和aggregate。message_and_aggregate是需要自己Implement的,只有实现了它,才可以发挥矩阵计算的优势。
实例
接下来我举两个例子来说明pytorch geometric中的消息传递。
以下这段代码简单实现了邻域特征求和,并且实现了矩阵计算。
import torch
from torch_geometric.nn import MessagePassing
from torch_sparse import SparseTensor, matmul
class BigCatConv(MessagePassing):
def __init__(self):
super().__init__(aggr='add')
def forward(self, x, edge_index):
x = x
return self.propagate(edge_index, x=x)
def message(self, x_j):
print('message')
print('x_j:', x_j)
return x_j
def message_and_aggregate(self, adj_t):
print('message_and_aggregate')
return matmul(adj_t, x, reduce=self.aggr)
# 定义图的特征和边
x = torch.eye(4)
edge_index = torch.tensor([[1,2,3,3,0,0,0,1], [0,0,0,1,1,2,3,3]])
x
>>> tensor([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]])
model = BigCatConv()
out = model(x, edge_index)
>>> message
x_j: tensor([[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.],
[0., 0., 0., 1.],
[1., 0., 0., 0.],
[1., 0., 0., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.]])
out
>>>
tensor([[0., 1., 1., 1.],
[1., 0., 0., 1.],
[1., 0., 0., 0.],
[1., 1., 0., 0.]])
以上我们可以看到message函数被调用,最终节点特征是邻居节点特征的和。
我们再使用SparseTensor试试。
x = torch.eye(4)
edge_index = torch.tensor([[1,2,3,3,0,0,0,1], [0,0,0,1,1,2,3,3]])
adj_t = SparseTensor(row=edge_index[1], col=edge_index[0])
model = BigCatConv()
out = model(x, adj_t)
>>> message_and_aggregate
out
>>> tensor([[0., 1., 1., 1.],
[1., 0., 0., 1.],
[1., 0., 0., 0.],
[1., 1., 0., 0.]])
以上我们可以看到message_and_aggregate函数被调用,最终节点特征是邻居节点特征的和。
欢迎大家交流讨论,转载请注明出处。