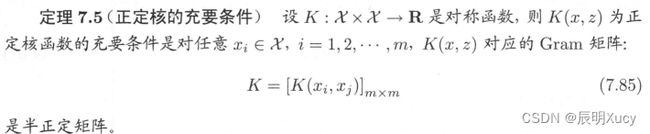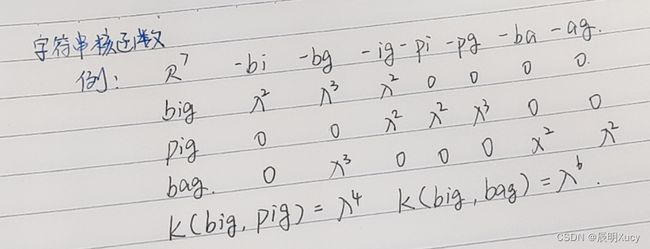统计学习方法 第七章支持向量机 读书笔记

第七章 支持向量机

支持向量机(support vector machines,SVM)是一种二分类模型

三要素

模型

定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机。

策略

间隔最大化。可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。

算法

求解凸二次规划的最优化算法

为什么叫支持向量机

7.1 线性可分支持向量机与硬间隔最大化

7.1.1 线性可分向量机

线性可分指的是可以完全分开，即超平面$\omega \cdot x+b=0$上没有样本点。

我们要使得最小几何间隔最大化

7.1.2函数间隔与几何间隔

定义

7.1.3 间隔最大化

• 凸优化问题指的是约束最优化问题

• 最大间隔分离超平面的存在与唯一性

**存在性：**由于训练数据中既有正类点又有负类点，所以（w，b）=（0，b）不是最优化的可行解，因此最优解必定满足w不等于0，由此可知分离超平面的存在性。

理解：$y(\omega \cdot x+b)>0为正确分类，\omega =0时,y(\omega \cdot x+b)-->yb$

​ $若b>0,负类无法正确分类，反之正类无法正确分类$

算法 7.1 最大间隔算法

7.1.4 学习的对偶问题

算法7.2 线性可分支持向量机学习算法

7.2 线性支持向量机与软间隔最大化

7.2.1 线性支持向量机

训练集：$T(x_1,y_1),(x_2,y_2),\cdot \cdot \cdot ,(x_N,y_N)$其中$x_i\in \mathcal{X}=R^n,y_i\in \mathcal{Y}=\{+1,-1\}$

线性可分：$y_i(\omega \cdot x_i+b)\ge 1$

位于间隔区域内的点：$y_i(\omega \cdot x_i+b)+{\xi }_i\ge 1此时{\xi }_i\in (0,1)$

位于间隔边界外(相反方向):$y_i(\omega \cdot x_i+b)+{\xi }_i\ge 1此时{\xi }_i>1,{\xi }_i为松弛变量$

此时约束条件：
KaTeX parse error: Can't use function '$' in math mode at position 2: $̲y_i(\omega·x_i+…

此时目标函数为：
$$\frac{1}{2}||\omega ||+C\sum _{i=1}^N{\xi }_i$$
C>0时称为惩罚参数，C值越大，对误分类惩罚越大，反之越小

此时优化问题：(凸二次规划问题)

7.2.2 原始问题与对偶问题

7.2.3 合页损失函数

7.3 非线性支持向量机与核函数

7.3.1 核技巧

非线性可分问题

不同于线性可分问题，存在一个超平面可使其分离，这里存在的是一个超曲面，称为非线性可分，同样的存在非线性不可分

核函数

映射$\varphi (x)$不唯一且维度也不唯一，但是他们对应的核函数相同

7.3.2 正定核

空间

正定核的充要条件

$$K(x,z)是正定核\iff K是半正定矩阵$$

7.3.3 常用核函数

3.定义在离散集合
$$[{\varphi }_n(s){]}_u={\Sigma }_{i:s(i)=u}{\lambda }^{l(i)}$$

7.3.4 非线性支持向量机

7.4 优化算法

7.4.1 序列最优化算法

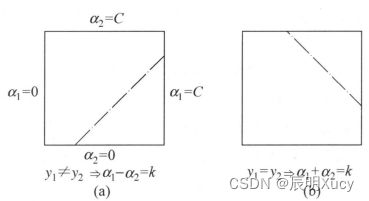
初始可行解为${\alpha }_1^o,{\alpha }_2^o,最优解为{\alpha }_1^n，{\alpha }_2^n$取值范围需要满足
$$L\le {\alpha }_2^n\le H$$

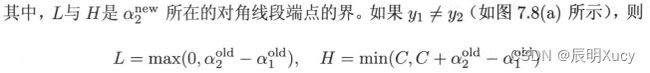
7.4.2 变量选择方法

1.第一个变量的选择

选择违反KKT条件最严重的样本点

2.第二个变量的选择

选择使$|E_1-E_2|$最大的${\alpha }_2$

3.b与$E_i$计算

当$0<{\alpha }_1^n<C$时

当$0<{\alpha }_2^n<C$

7.4.3 SMO