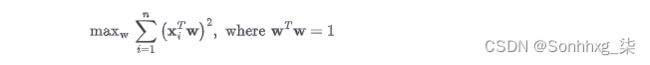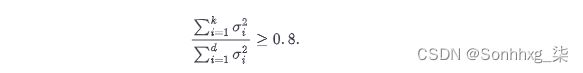【ML特征工程】第 6 章 ：降维：用 PCA 压缩数据薄饼

   大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流

个人主页－Sonhhxg_柒的博客_CSDN博客 

欢迎各位→点赞 + 收藏⭐️ + 留言​

系列专栏 - 机器学习【ML】 自然语言处理【NLP】  深度学习【DL】

​

 foreword

✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

如果你对这个系列感兴趣的话，可以关注订阅哟

文章目录

直觉

导航线性代数公式的技巧

推导

线性投影

方差和经验方差

主要成分：第一个配方

主成分：矩阵向量公式

主成分通解

转换特征

实施主成分分析

行动中的主成分分析

Whitening 和ZCA

PCA 的注意事项和局限性

根据核算方差选择 K

用例

概括

---

借助自动数据采集和特征生成技术，可以快速获取大量特征。  但并非所有这些都有用。在第3章和第4章中，我们讨论了基于频率的过滤和特征缩放作为修剪掉无信息特征的方法。现在我们将仔细研究使用主成分分析(PCA) 进行特征降维的主题。

本章标志着进入基于模型的特征工程技术。在此之前，大多数技术都可以在不引用数据的情况下定义。例如，基于频率的过滤可能会说，“去掉所有小于n的计数”，该过程无需数据本身的进一步输入即可执行。

另一方面，基于模型的技术需要来自数据的信息。例如，PCA 是围绕数据的主轴定义的。在前面的章节中，数据、特征和模型之间总是有着明确的界线。从这一点开始，差异变得越来越模糊。这正是当前特征学习研究令人兴奋的地方。

直觉

降维是关于在保留关键位的同时去除“无信息信息”。有很多方法可以定义“无信息”。PCA 关注线性相关的概念。在“矩阵剖析”中，我们将数据矩阵的列空间描述为所有特征向量的跨度。如果列空间与特征总数相比很小，那么大部分特征都是少数关键特征的线性组合。线性相关的特征会浪费空间和计算能力，因为信息本可以用更少的特征进行编码。为了避免这种情况，主成分分析试图通过将数据压缩到低维线性子空间中来减少这种“绒毛”。

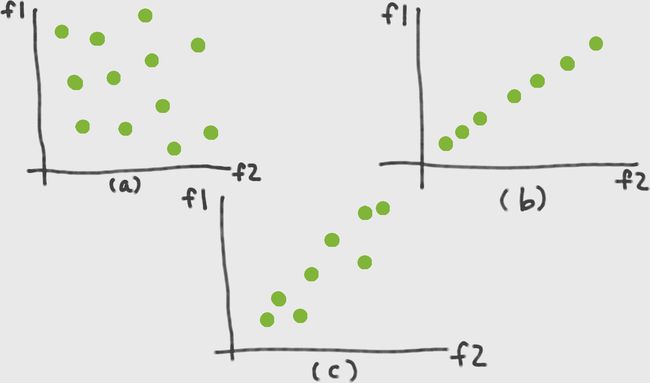
描绘特征空间中的数据点集。每个数据点都是一个点，整组数据点形成一个斑点。在图 6-1 (a) 中，数据点均匀地分布在两个特征维度上，并且 blob 填满了空间。在此示例中，列空间具有满秩。然而，如果其中一些特征是其他特征的线性组合，那么斑点看起来就不会那么丰满；它看起来更像图 6-1 (b)，一个扁平的斑点，其中特征 1 是特征 2 的副本（或标量倍数）。在在这种情况下，我们说 blob 的固有维数是 1，即使它位于二维特征空间中。

实际上，事物很少彼此完全相等。我们更有可能看到非常接近相等但不完全相等的特征。在这种情况下，数据 blob 可能类似于图 6-1 (c)。这是一个消瘦的斑点。如果我们想减少传递给模型的特征数量，那么我们可以用一个新特征替换特征 1 和特征 2，可能称为特征 1.5，它位于原始两个特征之间的对角线上。然后可以用一个数字（特征 1.5 方向上的位置）而不是两个数字f1和f2来充分表示原始数据集。

图 6-1。特征空间中的数据块：(a) 全秩数据块，(b) 低维数据块，和 (c) 近似低维数据块

这里的关键思想是用一些新特征替换冗余特征，这些新特征充分总结了原始特征空间中包含的信息。当只有两个特征时，很容易判断新特征应该是什么。当原始特征空间有数百或数千个维度时，这就更难了。我们需要一种方法来数学描述我们正在寻找的新功能。然后我们可以使用优化技术来找到它们。

从数学上定义“充分总结信息”的一种方法是说新数据块应尽可能多地保留原始数据量。我们正在将数据块压成一个扁平的煎饼，但我们希望煎饼在正确的方向上尽可能大。这意味着我们需要一种测量体积的方法。

体积与距离有关。但是一团数据点中的距离概念有些模糊。人们可以测量任意两对点之间的最大距离，但事实证明这是一个很难进行数学优化的函数。另一种方法是测量点对之间的平均距离，或者等效地，测量每个点与其均值（即方差）之间的平均距离。事实证明这更容易优化。（生活是艰难的。统计学家已经学会了走方便的捷径。）从数学上讲，这转化为最大化新特征空间中数据点的方差。

导航线性代数公式的技巧

要在线性代数的世界中保持方向性，请跟踪哪些量是标量，哪些是向量，以及向量的方向——垂直或水平。了解矩阵的维度，因为它们通常会告诉您感兴趣的向量是在行中还是在列中。在页面上将矩阵和向量绘制为矩形，并确保形状匹配。正如通过注意测量单位（距离以英里为单位，速度以英里/小时为单位）可以在代数中走得更远一样，在线性代数中，所有需要的都是维度。

推导

和以前一样，让X表示n × d数据矩阵，其中n是数据点的数量，d是特征的数量。令x为包含单个数据点的列向量。（因此x是X中其中一行的转置。）让v表示我们试图找到的新特征向量之一或主成分。

矩阵的奇异值分解 (SVD)

任何矩形矩阵都可以分解为三个具有特定形状和特征的矩阵：

X = UΣV T

这里，U和V是正交矩阵（即U T U = I和V T V = I）。Σ是包含X奇异值的对角矩阵，奇异值可以是正数、零或负数。假设X有n行和d列并且n ≥ d。那么U的形状为 n × d，而Σ和V的形状为d × d。（参见“奇异值分解 (SVD)”以全面了解 SVD 和矩阵的特征分解。）

线性投影

让我们休息一下下一步步推导PCA。图 6-2说明了整个过程。

图 6-2。PCA 示意图：(a) 特征空间中的原始数据；(b) 集中数据；(c) 将数据向量 x 投影到另一个向量 v 上；(d) 投影坐标的最大方差方向（等于 X T X 的主特征向量）

PCA 使用线性投影将数据转换到新的特征空间。图 6-2 (c) 说明了线性投影的样子。当我们将x投影到v上时，投影的长度与两者之间的内积成正比，由v的范数（它与自身的内积）归一化。稍后，我们将约束v具有单位范数。因此，唯一相关的部分是分子——我们称它为v（参见公式 6-1）。

 公式 6-1。投影坐标

z = x T v

请注意，z是标量，而x和v是列向量。由于有一堆数据点，我们可以将它们在新特征v上的所有投影坐标的向量z公式化（等式 6-2）。这里，X是熟悉的数据矩阵，其中每一行都是一个数据点。生成的z是一个列向量。

公式 6-2。投影坐标向量

z = X v

方差和经验方差

下一步是计算投影的方差。方差定义为均值平方距离的期望值（公式 6-3）。

公式 6-3。随机变量 Z 的方差

Var( Z ) = E[ Z – E( Z )] 2

有一个小问题：我们对问题的表述没有提及均值E(Z)；它是一个自由变量。一种解决方案是通过从每个数据点中减去平均值来将其从等式中删除。生成的数据集的均值为零，这意味着方差只是Z 2的期望值。从几何上讲，减去均值具有使数据居中的效果。（见图 6-2 (ab)。）

密切相关的量是两个随机变量Z 1和Z 2之间的协方差（公式 6-4）。将此视为将（单个随机变量的）方差概念扩展到两个随机变量。

公式 6-4。两个随机变量 Z 1和 Z 2之间的协方差

Cov( Z 1 , Z 2 ) = E[( Z 1 – E( Z 1 )( Z 2 – E( Z 2 )]

当随机变量的均值为零时，它们的协方差与它们的线性相关E[Z 1 Z 2 ]一致。稍后我们将更多地讨论这个概念。

方差和期望等统计量是在数据分布上定义的。实际上，我们没有真正的分布，只有一堆观察到的数据点，z 1 , ..., z n。这是称为经验分布，它为我们提供了方差的经验估计（公式 6-5）。

公式 6-5。Z 基于观测值 z 的经验方差

主要成分：第一个配方

结合公式 6-1中z i的定义，我们有最大化的公式公式 6-6中给出的预测数据的方差。（我们从经验方差的定义中删除分母n –1，因为它是一个全局常数，不会影响出现最大值的位置。）

公式 6-6。主成分的目标函数

 这里的约束强制w与自身的内积为1，相当于说向量必须有单位长度。这是因为我们只关心方向而不关心w的大小。w的大小是一个不必要的自由度，因此我们通过将其设置为任意值来摆脱它。

主成分：矩阵向量公式

接下来是棘手的步骤。公式 6-6中的平方和项相当繁琐。矩阵向量格式会更清晰。我们能做到吗？答案是肯定的。关键在于平方和恒等式：一堆平方项的和等于以这些项为元素的向量的范数平方，相当于向量与自身的内积。有了这个恒等式，我们可以用矩阵向量表示法重写公式 6-6，如公式 6-7所示。

公式 6-7。主成分的目标函数，矩阵向量公式

PCA 的这个公式更清楚地呈现了目标：我们寻找最大化输出范数的输入方向。这听起来很熟悉吗？答案在于X的奇异值分解(SVD) 。事实证明，最佳w是X的主左奇异向量，它也是X T X的主特征向量。投影数据称为原始数据的主成分。

主成分通解

这个过程可以重复。找到第一个主成分后，我们可以重新运行公式 6-7，并添加新向量与先前找到的向量正交的约束（请参见公式 6-8）。

公式 6-8。k+1 主成分的目标函数

解是X的第k +1 个左奇异向量，按奇异值降序排列。因此，前k个主成分对应于X的前k个左奇异向量。

转换特征

一旦找到主成分，我们就可以使用线性投影来转换特征。设X = UΣV T是X的 SVD ，V k是其列包含前k个左奇异向量的矩阵。X的维度为 n × d，其中d是原始特征的数量，而V k的维度为d × k。与公式 6-2中的单个投影向量不同，我们可以同时投影到投影矩阵（公式 6-9）中的多个向量上。

公式 6-9。PCA投影矩阵

 

 投影坐标矩阵很容易计算，并且可以使用奇异向量彼此正交的事实进一步简化（参见公式 6-10）。

公式 6-10。简单的 PCA 变换

 投影值只是前k个右奇异向量按前k个奇异值缩放。因此，可以通过X的 SVD 方便地获得整个 PCA 解决方案、组件和投影等。

实施主成分分析

PCA 的许多推导涉及首先将数据居中，然后对协方差矩阵进行特征分解。但实现 PCA 的最简单方法是对中心数据矩阵进行奇异值分解。

PCA 实施步骤

1. 将数据矩阵居中：

   C = X – 1μT _

   其中1是包含所有 1 的列向量，μ是包含X的行平均值的列向量。

2. 计算 SVD：

   C = UΣV T

3. 找出主要成分。前k个主成分是V的前k列；即，对应于k个最大奇异值的右奇异向量。

4. 转换数据。转换后的数据只是U的前k列。（如果需要白化，则按逆奇异值缩放向量。这要求所选奇异值不为零。请参阅“白化和 ZCA”。）

行动中的主成分分析

让我们通过将 PCA 应用于一些图像数据来更好地了解 PCA 的工作原理。MNIST数据集包含从 0 到 9 的手写数字图像。原始图像为 28 × 28 像素。图像的较低分辨率子集随scikit-learn一起分发，其中每个图像被下采样为 8×8 像素。scikit-learn 中的原始数据有 64 个维度。在示例 6-1中，我们应用 PCA 并使用前三个主成分可视化数据集。

示例 6-1。scikit-learn 数字数据集（MNIST 数据集的一个子集）的主成分分析

>>> from sklearn import datasets
>>> from sklearn.decomposition import PCA

# Load the data
>>> digits_data = datasets.load_digits()
>>> n = len(digits_data.images)

# Each image is represented as an 8-by-8 array. 
# Flatten this array as input to PCA.
>>> image_data = digits_data.images.reshape((n, -1))
>>> image_data.shape
(1797, 64)

# Groundtruth label of the number appearing in each image
>>> labels = digits_data.target
>>> labels
array([0, 1, 2, ..., 8, 9, 8])

# Fit a PCA transformer to the dataset.
# The number of components is automatically chosen to account for 
# at least 80% of the total variance.
>>> pca_transformer = PCA(n_components=0.8)
>>> pca_images = pca_transformer.fit_transform(image_data)
>>> pca_transformer.explained_variance_ratio_
array([ 0.14890594,  0.13618771,  0.11794594,  0.08409979,  0.05782415,
        0.0491691 ,  0.04315987,  0.03661373,  0.03353248,  0.03078806,
        0.02372341,  0.02272697,  0.01821863])
>>> pca_transformer.explained_variance_ratio_[:3].sum()
0.40303958587675121

# Visualize the results
>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.mplot3d import Axes3D
>>> %matplotlib notebook
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111, projection='3d')
>>> for i in range(100):
...     ax.scatter(pca_images[i,0], pca_images[i,1], pca_images[i,2], 
...                marker=r'${}$'.format(labels[i]), s=64)
    
>>> ax.set_xlabel('Principal component 1')
>>> ax.set_ylabel('Principal component 2')
>>> ax.set_zlabel('Principal component 3')

前 100 个投影图像显示在图 6-3的 3D 图中。标记对应于标签。前三个主成分约占数据集中总方差的 40%。这绝不是完美的，但它允许方便的低维可视化。我们看到 PCA 将彼此接近的相似数字分组。数字 0 和 6 与 1 和 7，以及 3 和 9 位于同一区域。空间大致分为一侧的 0、4 和 6，以及另一侧的其余数字。

图 6-3。MNIST 数据子集的 PCA 投影——标记对应于图像标签

由于数字之间存在大量重叠，因此很难在投影空间中使用线性分类器区分它们。因此，如果任务是对手写数字进行分类并且所选模型是线性分类器，那么前三个主成分不足以作为特征。然而，有趣的是看看 64 维数据集有多少可以仅在 3 维中捕获。

Whitening 和ZCA

由于目标函数中的正交性约束，PCA 转换产生了一个很好的副作用：转换后的特征不再相关。换句话说，特征向量对之间的内积为零。使用奇异向量的正交性很容易证明这一点：

 结果是一个对角矩阵，其中包含奇异值的平方，表示每个特征向量与其自身的相关性，也称为其ℓ 2范数。

有时，将特征的比例归一化为 1 也很有用。在信号处理术语中，这称为白化。它产生一组特征，这些特征与自身具有单位相关性并且彼此之间具有零相关性。从数学上讲，白化可以通过将 PCA 变换与逆奇异值相乘来完成（请参见公式 6-11）。

公式 6-11。PCA+ whitening

  whitening与降维无关；一个人可以在没有另一个的情况下执行一个。例如，零相位分量分析（ZCA）（Bell and Sejnowski，1996）是一种与 PCA 密切相关的白化变换，但不会减少特征数量。ZCA 白化使用完整的主成分集V而不进行缩减，并且包括一个额外的乘法返回到V T（公式 6-12）。

公式 6-12。ZCA whitening

 简单的 PCA 投影（公式 6-10）在新的特征空间中生成坐标，其中主要成分作为基础。这些坐标仅表示投影矢量的长度，而不表示方向。与主成分相乘得到长度和方向。另一个有效的解释是额外的乘法将坐标旋转回原始特征空间。（V是正交矩阵，正交矩阵在不拉伸或压缩的情况下旋转其输入。）因此，ZCA 生成尽可能接近（欧几里得距离）原始数据的白化数据。

PCA 的注意事项和局限性

使用 PCA 进行降维时，必须解决使用多少主成分 ( k ) 的问题。与所有超参数一样，这个数字可以根据生成模型的质量进行调整。但也有不涉及昂贵计算方法的启发式方法。

一种可能是选择k来解释总方差的所需比例。（此选项在 scikit-learn 包中可用PCA。）投影到第k个分量的方差为：

║ Xv k ║ 2 =║ u k σ k ║ 2 = σ k 2

这是X的第k个最大奇异值的平方。矩阵奇异值的有序列表称为它的谱。因此，要确定要使用多少分量，可以对数据矩阵执行简单的频谱分析并选择保留足够方差的阈值。

根据核算方差选择 K

要保留足够的分量以覆盖数据中总方差的 80%，请选择k使得

 另一种选择k的方法涉及数据集的固有维度。这是一个比较模糊的概念，但也可以从光谱中确定。基本上，如果频谱包含一些大的奇异值和一些小的奇异值，那么人们可能只收获最大的奇异值并丢弃其余的。有时频谱的其余部分并不小，但头部和尾部值之间存在很大差距。这也是一个合理的截止点。此方法需要对光谱进行目视检查，因此不能作为自动化管道的一部分执行。

对 PCA 的一个主要批评是转换相当复杂，因此结果难以解释。主成分和投影向量是实数值的，可以是正数也可以是负数。主成分本质上是（居中）行的线性组合，投影值是列的线性组合。例如，在股票收益应用程序中，每个因素都是股票收益时间片的线性组合。这意味着什么？很难为学习因素表达一个人类可以理解的原因。因此，分析师很难相信结果。如果你无法解释为什么你应该将其他人的数十亿资金投入特定股票，你可能不会选择使用该模型。

PCA 的计算成本很高。它依赖于 SVD，这是一个昂贵的过程。计算矩阵的完整 SVD 需要O ( nd 2 + d 3 ) 次操作（Golub 和 Van Loan，2012），假设n ≥ d——即，数据点多于特征。即使我们只需要k个主成分，计算截断的 SVD（k个最大的奇异值和向量）仍然需要O (( n+d ) 2 k ) = O ( n 2 k ) 次操作。当有大量数据点或特征时，这是禁止的。

很难以流方式、批量更新或从完整数据的样本中执行 PCA。SVD 的流式计算、更新 SVD 和从子样本计算SVD 都是困难的研究问题。算法是存在的，但以降低准确性为代价。一种含义是，当将测试数据投影到训练集中发现的主要成分时，人们应该期望较低的表示精度。随着数据分布的变化，人们将不得不重新计算当前数据集中的主要成分。

最后，最好不要将 PCA 应用于原始计数（字数、音乐播放数、电影观看数等）。这样做的原因是此类计数通常包含较大的异常值。（有一个粉丝观看了 314,582 次指环王的可能性非常高，这使其他计数相形见绌。）正如我们所知，PCA 寻找特征内的线性相关性。相关性和方差统计对大异常值非常敏感；一个大数字可能会大大改变统计数据。因此，最好先修剪大值数据（“基于频率的过滤”），或者应用缩放变换，如 tf-idf（第 4 章）或对数变换（“对数变换”）。

用例

PCA 通过寻找特征之间的线性相关模式来降低特征空间维度。由于涉及 SVD，PCA 计算超过几千个特征的成本很高。但是对于少量有实际价值的特征来说，是非常值得尝试的。

PCA 转换会丢弃数据中的信息。因此，下游模型的训练成本可能较低，但准确性较低。在 MNIST 数据集上，一些人观察到使用来自 PCA 的降维数据会导致分类模型不太准确。在这些情况下，使用 PCA 既有利也有弊。

最酷的之一PCA的应用是时间序列的异常检测。Lakhina 等人。(2004) 使用 PCA 检测和诊断互联网流量异常。他们专注于流量异常，即从一个网络区域到另一个网络区域的流量出现激增或下降时。这些突然的变化可能表明网络配置错误或协同拒绝服务攻击。无论哪种方式，了解此类更改发生的时间和地点对互联网运营商都很有价值。

由于互联网上的总流量如此之大，因此很难检测到小区域的孤立流量激增。一组相对较小的主干链路处理大部分流量。他们的主要见解是流量异常会同时影响多个链路（因为网络数据包需要跳跃通过多个节点才能到达目的地）。将每个链接视为一个特征，并将每个时间步长的流量作为度量。数据点是网络上所有链路的流量测量的时间片。该矩阵的主要组成部分表示网络上的整体流量趋势。其余分量表示包含异常的残差信号。

PCA 也经常用于金融建模。在这些用例中，它作为一种因素分析，这个术语描述了一系列统计方法，旨在使用少量未观察到的因素来描述观察到的数据变异性。在因子分析应用程序中，目标是找到解释成分，而不是转换后的数据。

股票收益等财务数量通常相互关联。股票可能同时上下波动（正相关），也可能反向波动（负相关）。为了平衡波动性和降低风险，投资组合需要一组彼此不相关的多样化股票。（不要把所有的鸡蛋都放在一个篮子里，如果那个篮子会沉下去的话。）找到强相关模式有助于决定投资策略。

股票相关模式可以是全行业的。例如，科技股可能会一起涨跌，而航空股往往会在油价高时下跌。但行业可能不是解释结果的最佳方式。分析师还在观察到的统计数据中寻找意想不到的相关性。特别地，统计因子模型(Connor, 1995) 在个股收益的时间序列矩阵上运行 PCA 以找到通常协变的股票。在此用例中，最终目标是主成分本身，而不是转换后的数据。

ZCA 在从图像中学习时作为预处理步骤很有用。在自然图像中，相邻像素通常具有相似的颜色。ZCA 白化可以去除这种相关性，这使得后续的建模工作可以专注于更有趣的图像结构。Krizhevsky (2009) 的论文“从图像中学习多层特征”包含很好的示例，这些示例说明了 ZCA 白化对自然图像的影响。

许多深度学习模型使用 PCA 或 ZCA 作为预处理步骤，尽管这并不总是必要的。在“用于自然图像建模的因式三向受限玻尔兹曼机”中，Ranzato 等人。(2010) 评论，“白化不是必需的，但可以加快算法的收敛速度。” 在“无监督特征学习中单层网络的分析”中，Coates 等人。(2011) 发现 ZCA 美白对某些模型有帮助，但不是全部。（注意本文中的模型是无监督特征学习模型，因此 ZCA 被用作其他特征工程方法的特征工程方法。方法的堆叠和链接在机器学习管道中很常见。）

概括

PCA 的讨论到此结束。关于 PCA 要记住的两个主要事情是它的机制（线性投影）和目标（最大化投影数据的方差）。解决方案涉及协方差矩阵的特征分解，这与数据矩阵的SVD密切相关。人们还可以通过将数据压成尽可能蓬松的煎饼来记住 PCA 。

PCA就是一个例子模型驱动的特征工程。（当目标函数进入场景时，人们应该立即怀疑模型潜伏在背景中。）这里的建模假设是方差充分表示数据中包含的信息。同样，该模型寻找特征之间的线性相关性。这在多个应用程序中用于减少相关性或找到输入中的共同因素。

PCA 是一种众所周知的降维方法。但它有其局限性，例如高计算成本和无法解释的结果。它作为预处理步骤很有用，尤其是当特征之间存在线性相关时。

当被视为消除线性相关性的方法时，PCA 与白化的概念有关。它的表亲 ZCA 以一种可解释的方式对数据进行白化处理，但不会降低维度。