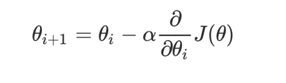线性回归算法及相关知识介绍
线性回归
一、算法简介
1、定义
利用回归方程,对多个自变量(特征)和因变量(目标)之间的关系进行建模的一种分析方式
· 只有一个自变量叫单变量回归,多个自变量叫多元回归
. 自变量和因变量之间有线性关系与非线性关系
. 线性关系分为单变量线性关系与多变量线性关系
2、公式
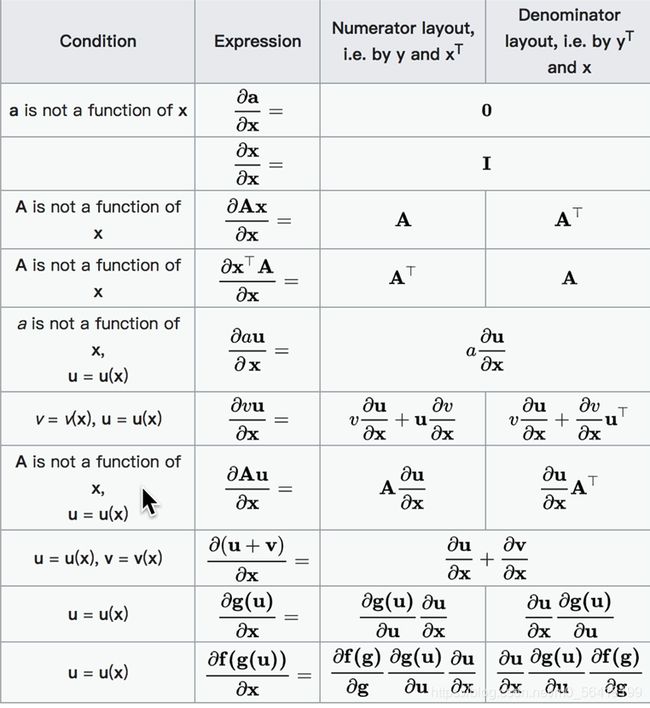
3、求导
二、线性回归损失与优化
1、损失求法
2、常用优化算法
3、算法简介
小规模数据选择正规方程(LinearRegression)(不能解决拟合问题),大规模数据选择**梯度下降(SGDRegressior)**算法(可能找到非最小值的极小值点)。
(1)正规方程
①公式
②使用中的问题
. 矩阵不可逆
原因1:所求参数大于样本数。
措施 :增加样本数。
原因2:特征值太多。
措施 :删除一些冗余的特征值。
. 样本量n太大
矩阵求逆的计算复杂度为O(n3),当样本量太大时,计算量过大,此时,不建议采用正规方程法。
. 函数太复杂
此时无法使用正规方程法。
③推导
④API
sklearn.linear_model.LinearRegression(fit_intercept=True)
回归系数
LinearRegression().coef_
是否计算偏置
fit_intercept=True
(2)梯度下降法
主要目的是通过迭代找到目标函数的最小值,或者收敛到最小值。
在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向。
①公式
α在梯度下降算法中被称作为学习率或者步长,步长太大会错过最低点,太小则会使到达最低点时间减慢
②简介
全梯度算法(FG)
计算所有样本误差,按照梯度下降,速度很慢,且无法进行超出内存容量限制的数据集,不能在线更新模型,及在运行过程中不能添加新的样本。
随机梯度算法(SG)
每次只代入计算一个样本目标函数的梯度来更新权重,重复这一过程,直到损失函数值停止下降或小于某一可接受的阈值。由于只使用一个样本进行迭代,容易受到噪声影响从而陷入局部最优解。
小批量梯度算法(mini-batch)
综合了SG与FG,每次取出一个小的样本集,在这个样本集上进行FG迭代更新权重。batch_size即为小样本集的大小,一般取2的幂次,利于GPU加速处理。不适合大数据训练,因为每一次梯度都与上一次无关。
随机平均梯度算法(SAG)
对每个样本的旧梯度都进行了维护,每次随机选择样本来更新新样本的梯度,同时使用所有样本梯度的平均值来更新参数。
其他:nesterov加速梯度下降法、动量法、Adagrad、Adadelta、RMSProp
③API
linear_model.SGDRegressor(loss='squared_loss',fit_intercept=True,learning_rate='invscaling',eta0=0.01)
loss=‘squared_loss’:损失类型,默认最小二乘法
fit_intercept=True:是否计算偏置
learning_rate=‘invscaling’:学习率
constant:常数,学习率等于eta0
invscaling:随着迭代自动更新学习率,eta=eta0/pow(t,power_t)
power_t默认为0.25
optimal:随着迭代自动更新学习率,eta=1/(α*(t+t0))
偏置
SGDRegressor().intercept_
回归系数
SGDRegressor().coef_
三、过拟合与欠拟合
1、欠拟合
模型过于简单,在训练集、测试集中表现都差
原因:学习到数据的特征过少
解决:
(1)增加特征数
通过“组合”、“泛化”、“相关性”来添加特征,同时,“上下文特征”、“平台特征”也是添加时的首选项
(2)添加多项式特征
在机器学习算法中使用的很普遍,例如线性回归时通过添加二次项或三次项来使模型泛化能力变强。
2、过拟合
模型过于复杂,在训练集中表现很好,测试集中表现很差
原因:原始特征过多,存在嘈杂特征,模型尝试兼顾所有特征
解决:
(1)重新清洗数据
过拟合也可能是由于数据不纯造成的,所以要重新清洗数据
(2)增大训练量
(3)正则化
(4)减少特征维度,防止维灾难(随纬度上升,分类器性能先上升,到达一点后便不断下降)
四、正则化
介绍:有些数据特征影响模型的复杂度,或者这个特征异常点较多,就要尽量减小这个特征的影响(甚至删除这个特征)
正则化力度越大,权重系数就越小
正则化力度越小,权重系数就越大
1、LASSO回归
L1回归
可以使某些w的值为0,删除其影响,倾向于消除完全不重要的权重
可以自动做出选择,输出一个稀疏模型(只有少数特征的权重为非0)
缺点:
在特征维度高于样本数或特征强相关时表现不佳

目标应使损失函数最小(minJ(θ)),所以使用一个较大的α就可以有效抑制θ的大小
API
from sklearn.linear_model import Lasso
2、Ridge Regression(岭回归)
L2回归
可以使某些w的值很小,趋近于0,削弱其影响
API
from sklearn.linear_model import Ridge
参数
fit_intercept=True:是否计算偏置
alpha=1.0:正则化力度(惩罚力度)0~ 1、1~10
solver:自动选择优化算法,若数据集大,数据多,一般自动选择sag(随即平均梯度下减)
normalize=True:是否进行标准化
属性
Ridge.coef_:回归权重
Ridge.intercept_:回归偏置
from sklearn.linear_model import RidgeCV
封装了交叉验证
增加参数alphas,可传入超参数组,进行交叉验证
3、Elastic net(弹性网络)
API
from sklearn.linear_model import ElasticNet
一般来说,我们应该避免使用朴素线性回归,对模型进行一定的正则化处理
4、Early Stopping
验证错误率,在错误率达到最小值(设置的阈值)时停止训练
五、案例
1、数据来源
加利福尼亚大学机器学习库
也可使用sklearn内置数据集load_boston
2、回归性能评估
3、正规方程实现
#导入数据集
from sklearn.datasets import load_boston
#数据分割
from sklearn.model_selection import train_test_split
#特征工程(标准化)
from sklearn.preprocessing import StandardScaler
#训练模型(正规方程)
from sklearn.linear_model import LinearRegression
#moxingpinggu(均方误差)
from sklearn.metrics import mean_squared_error
#模型保存及下载
import joblib
boston=load_boston()
boston_data=boston.data
boston_target=boston.target
x_train,x_test,y_train,y_test=train_test_split(boston_data,boston_target,test_size=0.2)
transfer=StandardScaler()
x_train=transfer.fit_transform(x_train)
x_test=transfer.transform(x_test)
estimator=LinearRegression()
estimator.fit(x_train,y_train)
print('正规方程模型系数为',estimator.coef_)
print('正规方程模型偏置为',estimator.intercept_)
predict=estimator.predict(x_test)
print('正规方程预测值是',predict)
error=mean_squared_error(y_test,predict)
print('正规方程均方误差为',error)
joblib.dump(estimator,'test.pkl')
4、梯度下降实现
使用invscaling,随着迭代自动更新学习率,eta=eta0/pow(t,power_t)
# 导入数据集
from sklearn.datasets import load_boston
# 数据分割
from sklearn.model_selection import train_test_split
# 特征工程(标准化)
from sklearn.preprocessing import StandardScaler
# 训练模型(梯度下降)
from sklearn.linear_model import SGDRegressor
# moxingpinggu(均方误差)
from sklearn.metrics import mean_squared_error
#模型保存及下载
import joblib
boston = load_boston()
boston_data = boston.data
boston_target = boston.target
x_train, x_test, y_train, y_test = train_test_split(boston_data, boston_target, test_size=0.2)
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
estimator = SGDRegressor(max_iter=1000)
estimator.fit(x_train, y_train)
print('梯度下降模型系数为', estimator.coef_)
print('梯度下降模型偏置为', estimator.intercept_)
predict = estimator.predict(x_test)
print('梯度下降预测值是', predict)
error = mean_squared_error(y_test, predict)
print('梯度下降均方误差为', error)
joblib.dump(estimator,'test.pkl')
5、岭回归实现
# 导入数据集
from sklearn.datasets import load_boston
# 数据分割
from sklearn.model_selection import train_test_split
# 特征工程(标准化)
from sklearn.preprocessing import StandardScaler
# 训练模型(进行标准化、交叉验证的岭回归)
from sklearn.linear_model import RidgeCV
# moxingpinggu(均方误差)
from sklearn.metrics import mean_squared_error
#模型保存及下载
import joblib
boston = load_boston()
boston_data = boston.data
boston_target = boston.target
x_train, x_test, y_train, y_test = train_test_split(boston_data, boston_target, test_size=0.2)
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
estimator = RidgeCV(alphas=(0.1,1.0,10),fit_intercept=True,normalize=False)
estimator.fit(x_train, y_train)
print('正规方程模型系数为', estimator.coef_)
print('正规方程模型偏置为', estimator.intercept_)
predict = estimator.predict(x_test)
print('岭回归预测值是', predict)
error = mean_squared_error(y_test, predict)
print('岭回归均方误差为', error)
joblib.dump(estimator,'test.pkl')