Notes on Optimal Transport (笔记)

摘要

本文翻译自 Notes on Optimal Transport，原文以生动的故事简要阐述了 Optimal Transport 的基本概念、求解方法、具体应用等，没有太过复杂的公式，非常适合新手入门。本文将原文翻译成中文，并进行精简、添加自己的理解，改动较大，如有理解不当或错误之处，还请指出。由于简化的原因，可能失去一定的故事性，建议先阅读更生动的原文。另外，我在后半部分记录了自己遇到的问题，深入解析了 OT 应用的具体细节。

简介

最优传输（Optimal Transport, OT），旨在以最小的代价将一个概率分布转化为另一个概率分布，在概率论、计算机视觉、机器学习、计算流体动力学和计算生物学等方面有广泛应用。代码：Github Repo.

甜点派对中的最优分配

有一些甜点，各种的量如下图所示：

5 种甜点，共 20 份，分给 8 个人，每个人能获得的甜点份数如下：

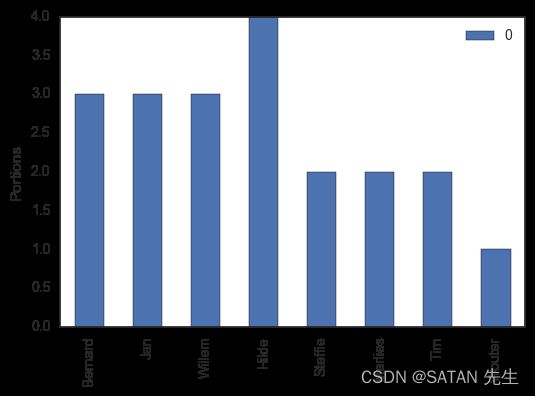
不同人对不同甜点的喜爱程度不同，用 [-2, 2] 的分数表示，分数越高越喜欢：

任务是：尽可能让大家分到自己喜爱的甜点，整体满意度最大化！

最优传输问题

引入一些概念：设向量 $\mathbf{r}=(3,3,3,4,2,2,2,1{)}^{⊺}$ 为每个人能获得的甜点份数，一般地，其维数为 $n$. 同理，向量 $\mathbf{c}=(4,2,6,4,4{)}^{⊺}$ 表示每种甜点的量，一般地，其维数为 $m$. 将这两个向量看作边缘概率分布，可归一化为概率单纯形，$sum(\mathbf{r})=1$, $sum(\mathbf{c})=1$。

$U(\mathbf{r},\mathbf{c})$ 是一个集合，包含了所有的甜点分配方案：
$$U(\mathbf{r},\mathbf{c})=\{P\in {\mathbb{R}}_{>0}^{n\times m}\mid P{1}_m=\mathbf{r},P^{⊺}{1}_n=\mathbf{c}\}\text{\hspace{1em}(1)}$$ $P$ 是一种分配方案，$P_{ij}>0$ 表示人 $i$ 分得甜点 $j$ 的量，那么，行求和 $sum(P_i)={\sum }_j{P}_{ij}$ 表示人 $i$ 获取的甜点总和，所以 $P{1}_m=\mathbf{r}$，即：对 $P$ 行求和就得到 $\mathbf{r}$；同理，列求和得到 $\mathbf{c}$。

【注】：每份甜点还可以继续细分，不一定一整份地分给一个人。

每个人对不同甜点的喜爱程度存储在代价矩阵 $M\in {\mathbb{R}}^{n\times m}$ 中，但这里求最小代价，将喜爱程度矩阵取负便可以看作代价。即：$M_{ij}$ 表示人 $i$ 获取甜点 $j$ 时的满意度的负。

那么总的最小代价是：
$$d_M(\mathbf{r},\mathbf{c})=\underset{P\in U(\mathbf{r},\mathbf{c})}{\min }\sum _{i,j}{P}_{ij}{M}_{ij}\text{\hspace{1em}(2)}$$ 这就叫 $\mathbf{r}$ 和 $\mathbf{c}$ 之间的最小传输，可以用简单的线性规划求解。$d_M(\mathbf{r},\mathbf{c})$ 被称为 Wasserstein Metric（瓦斯距离），是两个概率分布之间的距离。

【注】：其实这就是线性规划问题，$d_M(\mathbf{r},\mathbf{c})$ 是一个线性函数，自变量是 $P$，规定 $P\in U(\mathbf{r},\mathbf{c})$，也即限定自变量范围，然后求一个最小值，和初中学的线性规划数学题很像。但有一个问题，$P\in U(\mathbf{r},\mathbf{c})$ 即 $P{1}_m=\mathbf{r},P^{⊺}{1}_n=\mathbf{c}$，所限定的区域是什么样子的？

每样甜点都尝尝（均匀化倾向）

把上面的 Wasserstein Distance 公式加一项：
$$d_M^{\lambda }(\mathbf{r},\mathbf{c})=\underset{P\in U(\mathbf{r},\mathbf{c})}{\min }\sum _{i,j}{P}_{ij}{M}_{ij}-\frac{1}{\lambda }h(P)\text{\hspace{1em}(3)}$$ 称为 Sinkhorn Distance. $h(P)=-{\sum }_{i,j}{P}_{ij}\log P_{ij}$ 是 $P$ 的信息熵。熵越大，分布越均匀，甜点分配越趋向于均分。参数 $\lambda$ 决定 “尽可能满足每个人的甜点口味” 和 “均匀分配甜点” 之间的 trade-off. 这类似于正则化，这使 Sinkhorn Distance 在一些情况下比 Wasserstein Distance 好使。这是因为一个自然的先验知识：如果不考虑代价，一切都应该是均匀的！

求解 Sinkhorn Distance 的优雅算法

由于增加了商正则化项，在某种程度上，求解变复杂了。但有一个高效的算法可以求解 $P_{\lambda }^{\star }$ 和对应的 $d_M^{\lambda }(\mathbf{r},\mathbf{c})$! 算法来源于一种现象：最优传输矩阵 $P_{\lambda }^{\star }$ 的元素有一种形式
$$(P_{\lambda }^{\star }{)}_{ij}={\alpha }_i{\beta }_j{e}^{-\lambda M_{ij}}\text{\hspace{1em}(4)}$$ 其中 ${\alpha }_1,\dots ,{\alpha }_n$ 和 ${\beta }_1,\dots ,{\beta }_n$ 是一些待定的常量，使 $P$ 满足条件 $\{P{1}_m=\mathbf{r},P^{⊺}{1}_n=\mathbf{c}\}$。

Sinkhorn knopp 算法：

至于为什么是这样的解法，以后再看吧。

代码：

def compute_optimal_transport(M, r, c, lam, epsilon=1e-8):
    """
    Computes the optimal transport matrix and Slinkhorn distance using the
    Sinkhorn-Knopp algorithm

    Inputs:
        - M : cost matrix (n x m)
        - r : vector of marginals (n, )
        - c : vector of marginals (m, )
        - lam : strength of the entropic regularization
        - epsilon : convergence parameter

    Outputs:
        - P : optimal transport matrix (n x m)
        - dist : Sinkhorn distance
    """
    n, m = M.shape
    P = np.exp(-lam * M)
    P /= P.sum()
    u = np.zeros(n)
    # normalize this matrix
    while np.max(np.abs(u - P.sum(1))) > epsilon:  # 有个小 bug
        u = P.sum(1)
        P *= (r / u).reshape((-1, 1))
        P *= (c / P.sum(0)).reshape((1, -1))
    return P, np.sum(P * M)

计算甜点分配结果：

$\lambda =10$，熵正则化项权重 0.1 较小，均匀化趋势不明显，所以，每个人只获得了自己喜欢的甜点。比如，Jan 获得了三份 carrot cake（她唯一打正分的甜点），剩下的一份 carrot cake 给了 Tim，他是除了 Jan 之外唯一给 carrot cake 正分的人。

如果减小参数 $\lambda$，则增加熵项权重，分配会更加均匀化：尝一尝自己不那么喜欢的甜点。

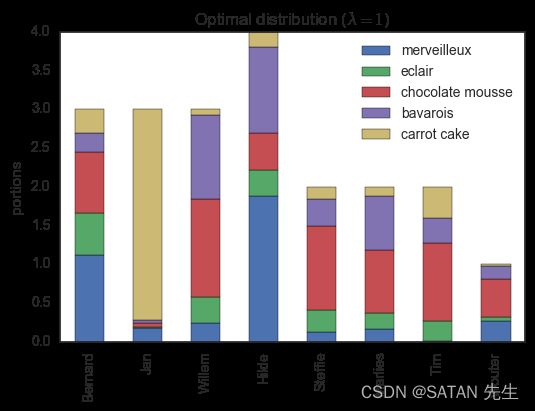
$\lambda =1$ 使熵正则化项获得了大的权重，分配趋于均匀化。

有无熵正则化的几何解释（这就是刚才所问的：所限定的区域是什么样子的？）：

$$有无熵正则化的几何解释$$ 代价矩阵决定了哪个方向的 $P$ 更好，集合 $U(\mathbf{r},\mathbf{c})$ 是解空间，无熵正则化时，$P^{\star }$ 往往在解空间的一个角。有熵正则化时，则 $P^{\star }$ 在红圈上。特别地，当 $\lambda \to \infty$，$P_{\lambda }^{\star }$ 趋于 $P^{\star }$；当 $\lambda \to 0$，仅考虑熵项，$P_{\lambda }^{\star }=\mathbf{r}{\mathbf{c}}^{⊺}$，即绝对地均匀分配。

【注】：至于为什么解空间是这样，解为什么会落在角上？以后再说吧。（回想中学的线性规划题）

OT 的应用

根据目的，应用分为两类：matching distributions (being interested in $P_{\lambda }^{\star }$) or computing a distance between distributions (being interested in $d_M^{\lambda }(\mathbf{r},\mathbf{c})$. 想要分配方案，就是分布匹配；想要距离，就是计算分布之间的距离。

Matching Distributions

[Interpolate Data] 一种分布转换为另一种分布的方案。 对数据科学家来说，最常见的分布是简单的数据集：在某空间中的一些点，它们有相同的权重。下面是一个例子，两个数据集的数据点分别围绕在两个不同半径的同心圆附近。

根据欧氏距离 softly 匹配两个数据集中的点。这有什么用呢？假设你想在两个数据集之间插入一个新的数据集 set 3。This can be done by merely taking a weighted average between each point of the first set and its analogs of set 2.（这个待会儿通过代码讲一下怎么插入的）

【注】：softly，由于两个数据集中的点数量可能不一致，且一个点也未必就只能匹配另一数据集中的一点。最简单地，set1 有一个点，set2 有两个点，那么 set1 中的点以不同的比例(权重)匹配 set2 中的两个点。==>> 既然如此，怎么在 set1 中的一个点和 set2 中的两个点之间插入数据集？（待会儿看代码）

[Domain Adaptation] 训练集的图象是白天的，测试集的图象是夜晚的，这叫 domain shift，即，训练集和测试集的分布不一样。

解决方案：

1. 用 OT 链接训练集和测试集中的实例；
2. 通过最小化 Wasserstein or Sinkhorn Distance 学习一个从训练分布到测试分布的 mapping；然后将训练集映射（转换）到与测试集相同的分布；
3. 在匹配分布后的训练集上建立分类器。

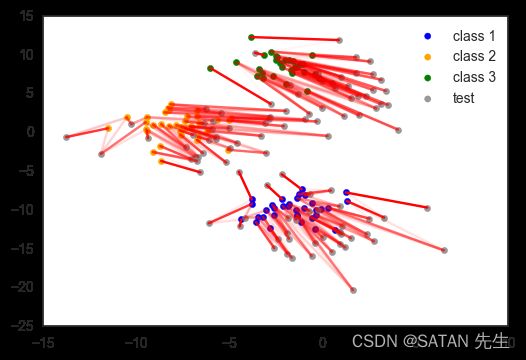
例子：数据集中有三个类别，训练集和测试集之间存在 domain shift，通过 OT 匹配训练与测试分布后，学习就容易多了。

[颜色转换]：改变一个图像的配色方案，使其与另一个图像相匹配。我们简单地将图像表示为三维颜色空间中的像素分布。与 domain 传输类似，我们可以使用最优传输和一个简单的多元回归方法将一个配色方案映射到另一个配色方案。简单快速！虽然效果不怎么样。待会儿代码解释！

作者还将 OT 用于 model species interaction networks，不过代码是用 Julia 语言写的，以后再看吧。

Finding a Distance Between Two Distributions

计算分布之间的距离时，通常用 Kullback-Leibler 散度，但瓦瑟斯坦或辛霍恩距离是更灵活的方法：损失函数中的代价矩阵允许我们将有价值的先验知识合并到度量中!

例如，假设您想比较不同的食谱，每个食谱都是一组不同的食材，两种食材之间有一定的距离或相似之处，但你如何比较不同的食谱呢？简单！用 OT，这基本上可以归结为把一个食谱变成另一个食谱所需的努力。食谱中每种食材的相对含量就是边缘分布。

References

Courty, N., Flamary, R., Tuia, D. and Rakotomamonjy, A. (2016). Optimal transport for domain adaptation. arxiv
Cuturi, M. (2013) Sinkhorn distances: lightspeed computation of optimal transportation distances. arxiv
Lévy, B. and Schwindt, E. (2017). Notions of optimal transport theory and how to implement them on a computer. arxiv

翻译完毕！

---

以下是一些问题思考以及代码解释

---

$U(\mathbf{r},\mathbf{c})=\{P\in {\mathbb{R}}_{>0}^{n\times m}\mid P{1}_m=\mathbf{r},P^{⊺}{1}_n=\mathbf{c}\}$，所限定的区域是什么样子的？

Wasserstein Distance 本质上就是线性规划问题，$U(\mathbf{r},\mathbf{c})$ 是线性规划问题的可行域。接下来我们就看一看它怎么就是线性规划问题了？可行域是啥样子？

从 OT 的定义 “求两个概率分布之间的距离” 来看，公式 $(2)$ 中，$d_M(\mathbf{r},\mathbf{c})$ 是自变量 $\mathbf{r}$ 和 $\mathbf{c}$ 以及 $M$ 的函数，其中 $\mathbf{r}$ 和 $\mathbf{c}$ 限定为概率单纯形（概率分布）。给定了这些自变量，就能确定最小距离 $d_M(\mathbf{r},\mathbf{c})$。如果这样看，确实看不到明显的线性规划的影子。
换个角度看，给定了 $\mathbf{r}$ 和 $\mathbf{c}$ 以及 $M$ 后，我们把 $P$ 看作自变量，每个 $P_{ij}$ 都是一个自变分量，$M$ 是权重，那么 $d_M(\mathbf{r},\mathbf{c})$ 就是 $P$ 的线性函数，而 $U(\mathbf{r},\mathbf{c})=\{P\in {\mathbb{R}}_{>0}^{n\times m}\mid P{1}_m=\mathbf{r},P^{⊺}{1}_n=\mathbf{c}\}$ 就是可行域，任务就是从可行域内找到一个最佳的 $P$，使 $d$ 最小。

举例
给定 $\mathbf{r}=\{0.4,0.6\}$，$\mathbf{c}=\{0.2,0.3,0.5\}$，$M=\left[\begin{array}{ccc}7& 4& 3\\ 6& 8& 5\end{array}\right]$，$P=\left[\begin{array}{ccc}{p}_1& p_2& p_3\\ p_4& p_5& p_6\end{array}\right]$，则
$$\begin{gathered} d(P)=7p_1+4p_2+3p_3+6p_4+8p_5+5p_6 \\ s.t.\{\begin{array}{cc}& p_1+p_2+p_3=0.4\\ & p_4+p_5+p_6=0.6\\ & p_1+p_4=0.2\\ & p_2+p_5=0.3\\ & p_3+p_6=0.5\\ & p_i>0,i\in \{1,2,3,4,5,6\}\end{array} \end{gathered}$$

实打实的线性规划了吧！接下来看看 $U(\{0.4,0.6\},\{0.2,0.3,0.5\})$ 及 $p_i>0$ 所限定的可行域使什么样子。一看，等式部分是线性方程组$$\left[\begin{array}{cccccc}1& 1& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 1\\ 1& 0& 0& 1& 0& 0\\ 0& 1& 0& 0& 1& 0\\ 0& 0& 1& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{p}_1\\ p_2\\ p_3\\ p_4\\ p_5\\ p_6\end{array}\right]=\left[\begin{array}{c}0.4\\ 0.6\\ 0.2\\ 0.3\\ 0.5\end{array}\right]$$ 一般情况下，可以求得这个线性方程组的解系，再加上 $p_i>0$ 的限制，就是可行域。

可行域是什么样子的？是不是真的像上文中 “有无熵正则化的几何解释” 图中的那样子？咱们掰开看看。我们知道，一般线性方程组求解时，经过初等行变换，最后留下几个自由变量，其他变量可由自由变量表示，再由自由变量的向量基表示整个解系。说了这些，还是不知道可行域是啥样子。那就举例子，由于人最多也就能在脑海里浮现 3D 图象（更高维的你没见过），那就在 3D 空间中看看吧。假如我们解一个三个自变量的线性方程组，化到最后，变成了这样 $$\left[\begin{array}{ccc}1& 0& -3\\ 0& 1& -2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}0.4\\ 0.5\end{array}\right]$$ 则 $$\{\begin{array}{c}{x}_1=3x_3+0.4\\ x_2=2x_3+0.5\end{array}\text{\hspace{1em}(c1)}$$ 一个自由变量($x_3$)，其他两个被 $x_3$ 确定，好熟悉啊，这是啥？不就是参数方程嘛。嗯！是个参数方程，它表示了 3D 空间中的一根直线，我再添上 $x_i\in (0,1)$ 的限制，就成了一条线段。那如果是两个自由变量呢？比如，线性方程组最后化成了这样 $$\left[\begin{array}{ccc}1& -3& -4\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}0.6\end{array}\right]$$
则把 $x_2$ 和 $x_3$ 看作自由变量，得到 $x_1=3x_2+4x_3+0.6$，这是 3D 空间中的面。下一步就到更高维，我们无法想象是什么样子。即使是 4D 空间，看参数方程 $$\{\begin{array}{c}{x}_1=a\ast x_4+b\\ x_2=c\ast x_4+d\\ x_3=e\ast x_4+f\end{array}\text{\hspace{1em}(c1)}$$ 也仅仅能知道这是一条超直线。如若是两个自由变量 $$\{\begin{array}{c}{x}_1=a\ast x_3+b\ast x_4+c\\ x_2=d\ast x_3+e\ast x_4+f\end{array}$$ 我们单看一个参数方程，可以知道是一个平面（丢掉 1 维），但两个方程一块，是什么？我现在只能类推：对于一个自由变量的参数方程（$c1$），单个方程（如 $x_1=a\ast x_4+b$）表示坐标平面 ($x_1,x_2$) 上的直线，多个这样的直线组合起来（参数方程组）是更高维空间中的直线，那么，多自由变量的参数方程组，应该是超平面，所以 “有无熵正则化的几何解释” 的那张图这么画没什么问题。

总的来说，线性函数沿着超平面单调，单调方向由 $M$ 决定，就像直直的滑滑梯，坐上就会往下滑，直到遇到底部边缘，但更多的是一个角（底子平平的概率比较小），所以：如果没有熵正则化，最优解会在某个角落（或者平底锅的底上）。$\mathbf{r}{\mathbf{c}}^{⊺}$ 是可行域内的一个解，代表着均匀分配，但它大概率不是最优解，熵正则化会使 $P$ 朝着 $\mathbf{r}{\mathbf{c}}^{⊺}$ 前进。整个辛霍恩距离的优化就成了：在可行域的超平面上放一颗小球，它滚向最优解的角落；$\mathbf{r}{\mathbf{c}}^{⊺}$ 处打了一颗钉子，用一根皮筋拴住了小球；皮筋越松球就越向最优的角落滑去，皮筋越紧就越将小球拉向钉子。$\lambda$ 控制着皮筋的松紧。

Sinkhorn-Knopp 求解器

先看 “至于为什么是这样的解法，以后再看吧”

为什么这样可以求解 OT 的辛霍恩距离？说不清，但这可以联想到基于 softmax 的自适应采样法：

假设有 n 个样本，我们希望 loss 更大的样本在总的损失函数中有更高的权重，即，获得更高的采样权重，以更快地优化这些 loss 更大的样本。那么
$$\begin{gathered} weight(x_i)=\frac{exp(\lambda \ast loss(x_i))}{{\sum }_1^{n}exp(\lambda \ast loss(x_j))} \\ total\_loss(X)=weights(X)\ast loss(X) \end{gathered}$$ 其中 weights 不参与梯度计算。$\lambda$ 值越大，这种 “高损失获取高采样权重” 的效果就越明显。

再回到 OT 求解问题，先不管最优解的形式 $(P_{\lambda }^{\star }{)}_{ij}={\alpha }_i{\beta }_j{e}^{-\lambda M_{ij}}$，我们先看其计算的初始化 $$initialize:P_{\lambda }=e^{-\lambda M}$$ 从这个初始化中，我们可以看到 “基于 softmax 的自适应采样法” 的影子，只不过里面多了个负号，这不要紧，本质时一样的，再看代码里有一行 P /= P.sum()，妥妥的 softmax 函数。整个来看，初始化的目的是：$M_{ij}$ 越大（代价越大），初始化的 $P_{ij}$ 越小，反之越大，而 $\lambda$ 越大，这种趋势越明显。当 $\lambda \to 0$，就是均匀分布，对应了距离公式中的 “仅考虑熵项”； 当 $\lambda \to \infty$，将这种趋势放到最大，对应了距离公式中的 “不考虑熵项”。

代码中有个小 bug

乍一看代码没有问题，在实际的运行中也正常。但我把 $\lambda$ 调到很大（甜点实验中 $\lambda =100$），会发现最终的结果不满足 $P{1}_m=\mathbf{r}$，不是误差，差别很大。我也检查了是不是由于 $\lambda$ 太大导致溢出了，结果发现不是。实际上 $\lambda =28.5$ 时就出现了这种现象。当设置更小的 epsilon 时，计算结果又恢复正常。奇怪！

仔细观察代码，设置的循环停止条件是 np.max(np.abs(u - P.sum(1))) > epsilon，这个条件仅仅说明 P.sum(1) 的更新变慢了，更新量小于 epsilon，并不能说明循环已经达到解空间条件 $P{1}_m=\mathbf{r}$。在循环条件上加上一条 np.max(np.abs(r - P.sum(1))) > epsilon，应该万事无忧了吧！

再记录一点，我把代码改成了这样

u = P.sum(axis=1, keepdims=True)
v = P.sum(axis=0, keepdims=True)
# normalize this matrix
while np.max(np.abs(r - u)) + np.max(np.abs(c - v)) > epsilon:
	u = P.sum(axis=1, keepdims=True)
	v = P.sum(axis=0, keepdims=True)  # 应放到行更新之后
	ot *= r / u  # 1/sum 归 1，*r 归 r
	ot *= c / v

发现不收敛了。究其原因，是因为循环中 v 的计算放在了 ot *= measure_r / u 之前，这样 ot *= measure_c / v 就不能 # 1/v 归 1，*c 归 c 了，归不到 c，自然就不收敛了？

How to Interpolate Data？

如何利用 Distribution Matching 分布匹配来 Interpolate Data？我们先看 Distribution Matching 代码：

# two concentric circles
points, labels = datasets.make_circles(n_samples=100, noise=0.05, factor=0.6, shuffle=False)
points_0 = points[labels == 0]
points_1 = points[labels == 1]
n, m = len(points_0), len(points_1)

r = np.ones(n) / n  # 都是均匀分布的
c = np.ones(m) / m  # 相同权重
cost_matrix = spatial.distance_matrix(points_0, points_1)  # 数据点两两之间的距离作为 cost
ot, od = sinkhorn_distance(cost_matrix, r, c, lam=10, epsilon=1e-5)

上述代码生成分别围绕俩个同心圆的数据点集（$points\_0$ 和 $points\_1$）

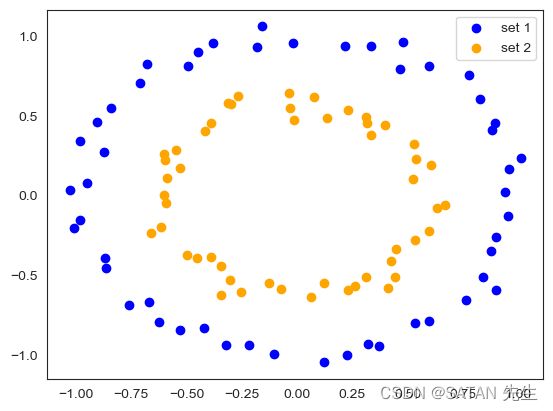
任务就是：以最小的代价（距离最短）将 set1 和 set2 中的点连接起来。这似乎脱离了原本 “货物运输” 或 “推土距离” 的概念。那我们就给他恢复这种概念，把这些点想象成一堆堆的小土堆，如何以最小的代价将 “土堆集” set1 变成 “土堆集” set2？点与点之间运送的土量就是连接强度。既然同一集合中小土堆都一样（没有谁是特别的），那它们的土量都是一样的。设土量为 1，set1 中有 n 个土堆，每个土堆的土量为 1/n，set2 中有 m 个土堆，每个土堆的土量为 1/m，运送土的代价就是两个土堆之间的距离。这样，set1 中的土堆就尽可能选择离自己近的 set2 中的土堆进行运输，即，set1 中的点尽可能选择离自己近的 set2 中的点进行连接。当然，OT 要求达到整体距离最短！

那么两个分布就是 r = np.ones(n) / n ，c = np.ones(m) / m，代价矩阵是 cost_matrix = spatial.distance_matrix(points_0, points_1) ，代入辛霍恩算法 sinkhorn_distance 就得到最优传输。计算结果 $P_{ij}$ 表示土堆 $i$ 运送给土堆 $j$ 的土量，也可以说 “点 $i$ 与点 $j$ 的连接强度”。

重点来了，怎么在两个数据集中间插入新的数据集？两个数据集中的点的数量不一定一致，一个点也未必就连接一个点。来看看原文怎么说：“taking a weighted average between each point of the first set and its analogs of set 2”. 翻译过来就是 “取第一个集合的每一个点与第二个集合的相似点之间的加权平均值”，咋一听有道理，但实际上什么是第二个集合的相似点？阅读代码，发现是这么写的：

mixing = self.P.copy()
mixing /= self.r.reshape((-1, 1))
X = (1 - alpha) * self.X1 + alpha * mixing @ self.X2

可以看出，新数据集 X 是由 X1 和 mixing @ X2 的加权平均构建的，X1 就是 X1，那 mixing @ X2 是啥？我们重点关注 mixing @ X2，现在我们只知道其是一个与 X1 包含同样多点的数据集。mixing 是啥？是 $P/\mathbf{r}$，即 $P_i/{\mathbf{r}}_i$，由于 $P{1}_m=\mathbf{r}$，则每个 mixing[i] 都是概率单纯形，是点 $i$ 运往 X2 中各点的土量占点 $i$ 总土量的比例，也可以说，点 $i$ 与 X2 中各点的连接强度占点 $i$ 总连接强度的比例。

不是说是 “运送的土量”，是 “点之间的连接强度” 吗？怎么还跟数据点乘上了？我们知道，求两个点之间的加权平均是 $(1-\alpha )\ast x_1+\alpha \ast x_2$，代表两点连线上的一点，那多点的平均就是 ${\mathbf{p}}^{⊺}X$，其中 $X$ 是多个点，$\mathbf{p}$ 是概率单纯型。例如，同一个圆上的所有点的平均是圆心。mixing[i] @ X2 正是点 $i$ 在 X2 中 softly 连接的所有点的加权平均，可以认为是 “将点 $i$ 推到了位置 mixing[i] @ X2，那么 mixing @ X2 就是将整个数据集 X1 匹配到了 X2 相应的位置（换到了与 X2 相同的分布）。再取 X = (1-alpha) * X1 + alpha * mixing @ X2 就完成了 Interpolate Data. X 中点的数量与 X1 一致。当然也可以推 X2：

mixing = self.P.copy()
mixing /= self.c.reshape((1, -1))
X = (1 - alpha) * mixing.T @ self.X1 + alpha * self.X2

接下来让我们看一看，在 aplha=1 时，即 X = mixing @ X2 在不同 $\lambda$ 下是什么样子

$\lambda$ 越趋于 0，连接越均匀越发散， X = mixing @ X2 越趋于圆心（看 $\lambda =0.1$）。当 $\lambda =10$ 时，set1 中的点基本只连接与其比较近的几个点，X = mixing @ X2 也基本与 X2 保持相近。这样再执行 Interpolate Data 就说得通了。

如上图，这次的数据没有噪声，数据点标准地围绕在同心圆上，$\lambda =50$，基本忽略了熵项，每个蓝色点仅与最近的两个点匹配。在右子图中，绿色点是由 X = mixing @ X2 计算而得，即：将 set1 传输到与 set2 相同的分布，可以看到，每个绿色点是对应蓝色点的两个匹配点的加权平均，而红色点就是绿色点和红色点之间的插入点。

Domain Adaptation

在上一节中，我们彻底明白了分布转换是怎么回事，现在看 Domain Adaptation，就清晰多了。下面看一看具体怎么做吧。

在正常的分类数据集中，测试集和训练集分布是相同的，如图 1。分类时，我们训练一个 model，使相似的数据输入到 model 中能得到相同的类别。但测试数据 shift 后，如图 2，与训练数据分布出现较大偏差，则将其输入到 model 就无法准确得到数据的 class。可利用 OT 匹配训练数据和漂移的测试数据，如图 3，学习得到的 $P$ 可用于将一个分布转移到另一个分布。图 4 中，训练数据被转移到与漂移的测试数据同分布，这样就可以训练 model，然后进行测试。是不是和插入数据集一样的本质？

颜色转换流程

阅读了源代码，我整理了图片颜色转换的流程：

1. 将 RGB 图片 A 和 B 分别展平为 n*3 和 m*3 的矩阵，相当于 n（m） 个数据点，每个数据点是 (R, G, B) 像素点；
2. 各下采样 1000 个数据点，输入到 OT 计算，得到分布矩阵 P；
3. 用 P 与图片 A 的 采样数据点计算出图 B 在图 A 分布下的数据点；
4. 我们现在有：图 B 的 1000 个采样点，分别在 A 分布下 和 B 分布下，可以拿来训练一个模型，这个模型类似 P 的功能，将 B 分布下的数据转化到 A 分布下。
5. 将图 B 整个输入到 Predict Model，就可以将图 B 转化到 A 分布下，颜色转化完成。

问题 1：颜色转换到底是怎么转的？什么颜色又转换到了什么颜色？
答：回想前面的数据插入和漂移转换，由 OT 的计算过程来看，计算颜色 mapping 就是整个地以最小代价（颜色点的距离）计算两个图象的颜色距离，得到的 P 就可以用于颜色分布的转换。

问题 2：看起来 P 和 Predict Model 很像？
答：如此看来，颜色转换其实可以完全由 OT 完成，只不过，这可能计算量太大，所以采样 1000 点，通过 OT 转换这 1000 点，再由转换前后的 1000 点数据训练 Predict Model，则 Predict Model 也有了颜色映射的能力，且运算代价更小，可快速完成整张图的颜色转换。

def im2mat(image):
	"""Converts and image to matrix (one pixel per line)"""
	return image.reshape((-1, image.shape[-1]))

def mat2im(X, shape):
	"""Converts back a matrix to an image"""
	return X.reshape(shape)

def minmax(image):
	return np.clip(image, 0, 1)

def main():
	# read the images
	image_from = io.imread(config.image_file_from) / 256
	image_to = io.imread(config.image_file_to) / 256
	# get shapes
	shape_to = image_to.shape
	# flatten
	X_from = im2mat(image_from)
	X_to = im2mat(image_to)
	# number of pixes
	num_pixels_from = X_from.shape[0]
	num_pixels_to = X_to.shape[0]
	# subsample
	X_from_ss = X_from[np.random.randint(0, num_pixels_from, config.num_pixels), :]
	X_to_ss = X_to[np.random.randint(0, num_pixels_to, config.num_pixels), :]

	# optimal tranportation
	ot_color = ot.OptimalTransport(
		X_to_ss, X_from_ss, lam=config.lam,
		distance_metric=config.metric  # euclidean distance_metric
	)

	# model transfer
	transfer_model = neighbors.KNeighborsRegressor(n_neighbors=config.num_neighbors)
	trans_matrix = ot_color.P / np.expand_dims(ot_color.r, axis=-1)
	transfer_model.fit(X_to_ss, trans_matrix @ X_from_ss)  # subsample, 简化传输，再训练 KNN，预测转换
	X_transfered = transfer_model.predict(X_to)

	image_transferd = minmax(mat2im(X_transfered, shape_to))
	io.imsave(config.image_file_out, image_transferd)

if __name__ == '__main__':
	main()