深度强化学习CS285-Lec18 Meta-Learning in RL
Meta-RL
- 概述
- 一、问题定义
-
- 1.1 监督学习
- 1.2 元学习
- 1.3 Meta-Learning的数据集设定与学习方式
-
- 1.3.1 元学习的数据集是怎样的?
- 1.3.2 Meta-Learning的学习方式
- 1.4 Meta-Learning的一些理解
- 二、Meta-RL
-
- 2.1 问题描述:
- 2.2 Recurrence ( f f f为RNN, L L L为PG——Policy Gradient)
- 2.3 Optimization-Based( f f f为PG, L L L为PG)
- 2.4 Meta-Imitation Learning
-
- 2.4.1 f f f为Behavior Cloning, L L L为PG
- 2.4.2 f f f为Learned loss, L L L为PG
- 2.5 Meta-MBRL( f f f为SL with model, L L L为MPC)
- 2.6 Inference-Based ( f f f为Stochastic Encoder, L L L为SAC)
-
- 2.6.1 Meta-RL
- 2.6.2 POMDP
- 2.6.3 SAC
- 2.6.4 Inference-Based Method
- 三、总结
- 后记
概述
Meta-Learning为元学习,也称为Learning to learn,其目的是希望能从过去的任务经验中习得学习技巧,然后将学习技巧放在新任务上实现快速学习。
所以Meta-Learning的数据集设置,与standrad RL、标准的监督学习都不同。
Meta-Learning的一些定位:
- Transfer Learning的第三种方法,从Multi-Task中学习一些东西,然后Transfer到New Task
- 主要从Multi-Task中提炼知识,因此其数据集的设定非常特殊
- 对于New Task而言,只需要少量样本数据就能快速学习
本文介绍Meta-Learning从CV开始再到RL,在此之前先说清楚问题定义、Meta的来源。
一、问题定义
先记住几个符号:
- ϕ \phi ϕ为任务模型的参数, θ \theta θ为Meta模型的参数
- D D D为训练数据
1.1 监督学习
D = { ( x 1 , y 1 ) , ⋯ , ( x k , y k ) } D=\{(x_1,y_1),\cdots,(x_k,y_k)\} D={(x1,y1),⋯,(xk,yk)}, x x x为image, y y y为label
新任务目标为:
arg max ϕ l o g p ( ϕ ∣ D ) = arg max ϕ l o g p ( D , ϕ ) p ( D ) = arg max ϕ l o g p ( ϕ ) p ( D ∣ ϕ ) = arg max ϕ l o g p ( ϕ ) + l o g p ( D ∣ ϕ ) = arg max ϕ ∑ i l o g p ( y i ∣ x i , ϕ ) + l o g p ( ϕ ) \begin{aligned} \argmax_{\phi}logp(\phi|D)&=\argmax_\phi log\frac{p(D,\phi)}{p(D)}\\ &=\argmax_\phi log p(\phi)p(D|\phi)\\ &=\argmax_\phi logp(\phi)+logp(D|\phi)\\ &=\argmax_\phi \sum_ilogp(y_i|x_i,\phi)+logp(\phi)\\ \end{aligned} ϕargmaxlogp(ϕ∣D)=ϕargmaxlogp(D)p(D,ϕ)=ϕargmaxlogp(ϕ)p(D∣ϕ)=ϕargmaxlogp(ϕ)+logp(D∣ϕ)=ϕargmaxi∑logp(yi∣xi,ϕ)+logp(ϕ)
总结:监督学习是,在一个任务的数据集D上,最大化MAP学习模型参数 ϕ \phi ϕ(点估计,后续会引入Bayes)
1.2 元学习
D m e t a − t r a i n = { D 1 , . . . , D n } , D i = { ( x 1 i , y 1 i ) , ⋯ , ( x k i , y k i ) } D_{meta-train}=\{D_1,...,D_n\},D_i=\{(x_1^i,y_1^i),\cdots,(x_k^i,y_k^i)\} Dmeta−train={D1,...,Dn},Di={(x1i,y1i),⋯,(xki,yki)}
D n e w − t a s k = { ( x 1 , y 1 ) , ⋯ , ( x k , y k ) } D_{new-task}=\{(x_1,y_1),\cdots,(x_k,y_k)\} Dnew−task={(x1,y1),⋯,(xk,yk)}
加入多任务后的新任务目标为:
arg max ϕ l o g p ( ϕ ∣ D n e w − t a s k , D m e t a − t r a i n ) = arg max ϕ l o g ∫ p ( ϕ ∣ D n e w − t a s k , θ ) p ( θ ∣ D m e t a − t r a i n ) d θ ≈ arg max ϕ l o g p ( ϕ ∣ D n e w − t a s k , θ ∗ ) + l o g p ( θ ∗ ∣ D m e t a − t r a i n ) = arg max ϕ p ( ϕ ∣ D n e w − t a s k , θ ∗ ) \begin{aligned} &\argmax_\phi logp(\phi|D_{new-task},D_{meta-train})\\ &=\argmax_\phi log\int p(\phi|D_{new-task},\theta)p(\theta|D_{meta-train})d\theta\\ &\approx \argmax_\phi log p(\phi|D_{new-task},\theta^*)+logp(\theta^*|D_{meta-train})\\ &=\argmax_\phi p(\phi|D_{new-task},\theta^*) \end{aligned} ϕargmaxlogp(ϕ∣Dnew−task,Dmeta−train)=ϕargmaxlog∫p(ϕ∣Dnew−task,θ)p(θ∣Dmeta−train)dθ≈ϕargmaxlogp(ϕ∣Dnew−task,θ∗)+logp(θ∗∣Dmeta−train)=ϕargmaxp(ϕ∣Dnew−task,θ∗)
解释一下:
1. 目标为结合多任务的训练集 D m e t a − t r a i n D_{meta-train} Dmeta−train来学习新任务 D n e w − t a s k D_{new-task} Dnew−task的模型参数 ϕ \phi ϕ
2. 目标近似分解成两部分:从多任务中Meta-Learning的元模型参数 θ ∗ \theta^* θ∗,在元参数 θ ∗ \theta^* θ∗的条件下最大化新任务 D n e w − t a s k D_{new-task} Dnew−task的MAP目标
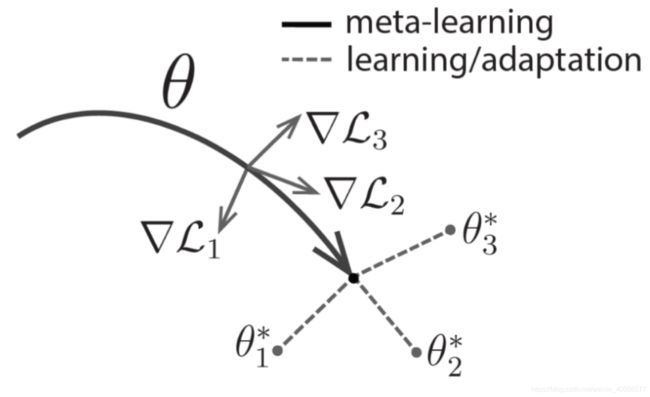
因此称 θ ∗ = arg max θ l o g p ( θ ∣ D m e t a − t r a i n ) \theta^*=\argmax_\theta logp(\theta|D_{meta-train}) θ∗=θargmaxlogp(θ∣Dmeta−train)为Meta-Learning Problem
而 ϕ ∗ = arg max ϕ l o g p ( ϕ ∣ D n e w − t a s k , θ ∗ ) \phi^*=\argmax_\phi logp(\phi|D_{new-task},\theta^*) ϕ∗=ϕargmaxlogp(ϕ∣Dnew−task,θ∗)为Adaptation Problem
1.3 Meta-Learning的数据集设定与学习方式
1.3.1 元学习的数据集是怎样的?
为了更好评价元模型参数,我们得对数据集设定清楚:
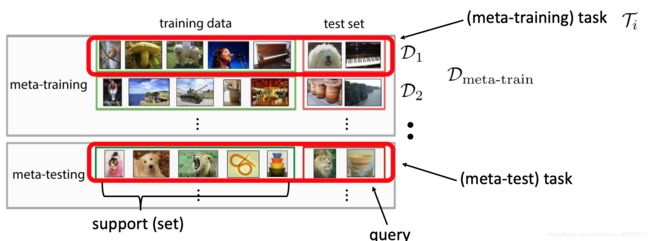
n个任务的 D m e t a − t r a i n = { ( D 1 t r , D 1 t s ) , . . . , ( D n t r , D n t s ) } D_{meta-train}=\{(D_1^{tr},D_1^{ts}),...,(D_n^{tr},D_n^{ts})\} Dmeta−train={(D1tr,D1ts),...,(Dntr,Dnts)},每一个任务 D i D_i Di都分为训练集 D i t r D_i^{tr} Ditr与测试集 D i t s D_i^{ts} Dits有,其中训练集有 k k k个样本,测试集有 l l l个样本,具体而言:
D i t r = { ( x 1 i , y 1 i ) , ⋯ , ( x k i , y k i ) } D i t s = { ( x 1 i , y 1 i ) , ⋯ , ( x l i , y l i ) } D_i^{tr}=\{(x_1^i,y_1^i),\cdots,(x_k^i,y_k^i)\}\\ D_i^{ts}=\{(x_1^i,y_1^i),\cdots,(x_l^i,y_l^i)\} Ditr={(x1i,y1i),⋯,(xki,yki)}Dits={(x1i,y1i),⋯,(xli,yli)}
于是每一个任务,现在简记为 T i = { D i t r , D i t s } \Tau_i=\{D_i^{tr},D_i^{ts}\} Ti={Ditr,Dits},或者 D i D_i Di,如下所示:
1.3.2 Meta-Learning的学习方式
为了评价 θ \theta θ,必须得通过 ϕ \phi ϕ,记住,在Meta-Train这一步我们只想要 θ ∗ = arg max θ l o g p ( θ ∣ D m e t a − t r a i n ) \theta^*=\argmax_\theta logp(\theta|D_{meta-train}) θ∗=θargmaxlogp(θ∣Dmeta−train),但是却没有关于 θ \theta θ的明确标签,因为一个样本 ( x , y ) (x,y) (x,y)的问题模型参数 ϕ \phi ϕ是由任务设定的,而 θ \theta θ是多任务的知识提取,因此需要用到多任务中的具体任务标签来进行评价,即通过 ϕ \phi ϕ来调整 θ \theta θ。
总结一句:多任务共有的元学习参数 θ \theta θ得通过第i个任务中设定的模型参数 ϕ i \phi_i ϕi进行评价并进行调整,因为只有每一个任务的label,而没有多任务的label
在用公式表述前,记 D t r = { D 1 t r , . . . , D n t r } , D t s = { D 1 t s , . . . , D n t s } , D m e t a − t r a i n = { D t r , D t s } D_{tr}=\{D_1^{tr},...,D_n^{tr}\},D_{ts}=\{D_1^{ts},...,D_n^{ts}\},D_{meta-train}=\{D^{tr},D^{ts}\} Dtr={D1tr,...,Dntr},Dts={D1ts,...,Dnts},Dmeta−train={Dtr,Dts}(在训练 θ \theta θ的时候,不需要使用到 D n e w − t a s k D_{new-task} Dnew−task)
Meta-Learning的General Form:
θ ∗ = arg max θ l o g p ( θ ∣ D t r , D t s ) ϕ ∗ = arg max ϕ l o g p ( ϕ ∣ D t r , θ ∗ ) \theta^*=\argmax_\theta logp(\theta|D^{tr},D^{ts})\\ \phi^*=\argmax_\phi logp(\phi|D^{tr},\theta^*) θ∗=θargmaxlogp(θ∣Dtr,Dts)ϕ∗=ϕargmaxlogp(ϕ∣Dtr,θ∗)
目标是学习一个多任务共有的 θ \theta θ使得单一任务上的 ϕ = f θ ( D i t r ) \phi=f_\theta(D^{tr}_i) ϕ=fθ(Ditr),与测试集 D t s D^{ts} Dts差不多,所以最重要的是下面的这个形式!一定要理解透!
θ ∗ = max θ ∑ i = 1 n l o g p ( ϕ i ∣ D i t s ) ϕ i = f θ ( D i t r ) \theta^*=\max_\theta \sum_{i=1}^nlogp(\phi_i|D_i^{ts})\\ \phi_i=f_\theta(D_i^{tr}) θ∗=θmaxi=1∑nlogp(ϕi∣Dits)ϕi=fθ(Ditr)
解释一下:
- 将第 i i i个任务的训练集 D i t r D^{tr}_i Ditr输入元模型 f θ f_\theta fθ,得到第 i i i个任务的问题模型参数 ϕ i \phi_i ϕi,然后根据测试集 D i t s D^{ts}_i Dits在第 i i i个任务上进行指标验证即 p ( ϕ i ∣ D i t s ) p(\phi_i|D_i^{ts}) p(ϕi∣Dits)
- 要学习的参数 θ \theta θ,应该要使n个任务的似然指标 ∑ i = 1 n l o g p ( ϕ i ∣ D i t s ) = ∑ i = 1 n l o g p ( D i t s ∣ ϕ i ) + l o g p ( ϕ i ) \sum_{i=1}^nlogp(\phi_i|D_i^{ts})=\sum_{i=1}^nlogp(D_i^{ts}|\phi_i)+logp(\phi_i) ∑i=1nlogp(ϕi∣Dits)=∑i=1nlogp(Dits∣ϕi)+logp(ϕi)最大
- 多任务共有的 θ \theta θ,通过单一任务 D i t r D_i^{tr} Ditr得到specified 任务的模型参数 ϕ i \phi_i ϕi,目的是找到这个 θ \theta θ使得到多任务的距离最短
对比一下,Meta-Learning与Multi-Task Learning中一种去学习多任务共同模型参数的方法相似:
- 当 f θ ( D i t r ) = θ f_\theta(D_i^{tr})=\theta fθ(Ditr)=θ即n个任务用一个模型参数 θ \theta θ去学,使n个任务评价最好,为multi-task Learning;
- 当 f θ ( D i t r ) = ϕ i f_\theta(D_i^{tr})=\phi_i fθ(Ditr)=ϕi即n个任务,每一个任务的模型参数 ϕ i \phi_i ϕi都不同,学习一个 θ \theta θ到 ϕ i \phi_i ϕi的映射使得,n个任务的评价最好
- 所以Multi-task的这种方法是Meta-Learning的一个Special Case
1.4 Meta-Learning的一些理解
- 一个网络的权重参数为 ϕ \phi ϕ,一个网络的超参数(batch、learning rate等)为 θ \theta θ
- 一个网络的权重参数为 ϕ \phi ϕ,一个网络的结构为 θ \theta θ
二、Meta-RL
2.1 问题描述:
-
Standrad RL:学习一个policy即 π θ \pi_\theta πθ
θ ∗ = arg max θ E π θ ( τ ) [ r ( τ ) ] = f R L ( M D P ) = f R L ( M ) \theta^*=\argmax_\theta E_{\pi_\theta(\tau)}[r(\tau)]=f_{RL}(MDP)=f_{RL}(M) θ∗=θargmaxEπθ(τ)[r(τ)]=fRL(MDP)=fRL(M) -
Meta-RL:学习一个Adaptation Rule即 f θ f_\theta fθ
θ ∗ = arg max θ E π ϕ i ( τ ) [ r ( τ ) ] ϕ i = f θ ( M D P i ) = f θ ( M i ) \theta^*=\argmax_\theta E_{\pi_{\phi_i}(\tau)}[r(\tau)]\\ \phi_i=f_\theta(MDP_i)=f_\theta(M_i) θ∗=θargmaxEπϕi(τ)[r(τ)]ϕi=fθ(MDPi)=fθ(Mi)
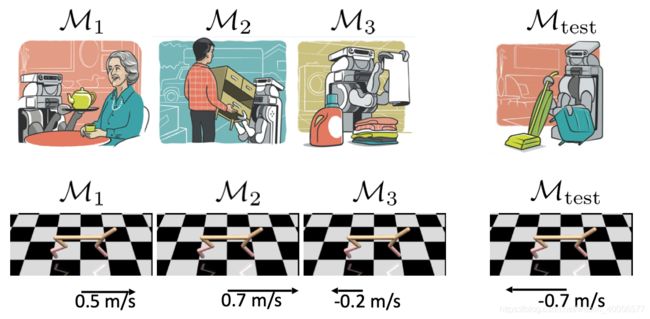
RL中一个task为一个 M D P = { S , A , P , r } MDP=\{S,A,P,r\} MDP={S,A,P,r},因此有 ( M t r a i n = { M 1 , M 2 , . . . , M n } , M t e s t ) (M_{train}=\{M_1,M_2,...,M_n\},M_{test}) (Mtrain={M1,M2,...,Mn},Mtest),如下:
于是Meta-RL有两个值得记住的循环:
- Meta-Training Outer Loop:
θ ∗ = arg max θ E π ϕ i ( τ ) [ r ( τ ) ] \theta^*=\argmax_\theta E_{\pi_{\phi_i}(\tau)}[r(\tau)] θ∗=θargmaxEπϕi(τ)[r(τ)] - Adaptation Inner Loop
ϕ i = f θ ( M i ) \phi_i=f_\theta(M_i) ϕi=fθ(Mi)
解释一下:
- Adaptation Rule就是指 f θ f_\theta fθ,利用来自 M i M_i Mi的轨迹 τ \tau τ来Adapt出 M i M_i Mi的policy parameters,可以Adapt几步
- 然后利用n个任务的轨迹各自Adapt出来了Policy以后即 π ϕ i ( τ ) \pi_{\phi_i}(\tau) πϕi(τ),根据 L L L(如最大expected reward)再对 f θ f_\theta fθ进行调整
Meta-RL的General Form:
- 从n个任务中Sample一个任务 i i i,收集该任务的真实轨迹 D i D_i Di(可以是专家数据,也可以是该任务的真实数据)
- 利用 D i D_i Di来对 θ \theta θ进行Adapt获得任务 i i i的策略参数 ϕ i = f θ ( D i ) \phi_i=f_\theta(D_i) ϕi=fθ(Di)
- 利用Adapted Policy即 π ϕ i \pi_{\phi_i} πϕi来当前Adapted的轨迹 D i ′ D_i' Di′
- 根据 D i ′ D_i' Di′与 ϕ i \phi_i ϕi来更新参数 θ \theta θ,即 θ = L ( D i ′ , ϕ i ) \theta=L(D_i',\phi_i) θ=L(Di′,ϕi)
因此下面围绕怎么选择Adaptation Rule即函数 f f f与损失函数 L L L来对算法类别进行划分:
2.2 Recurrence ( f f f为RNN, L L L为PG——Policy Gradient)

具体而言,Adaptation Model即元学习的模型参数为 θ \theta θ,用RNN模型来建模,然后用任务 i i i真实数据expert demons Adapt出策略的参数 ϕ i \phi_i ϕi,再根据Adapted Policy在任务中的表现来调整 θ \theta θ。
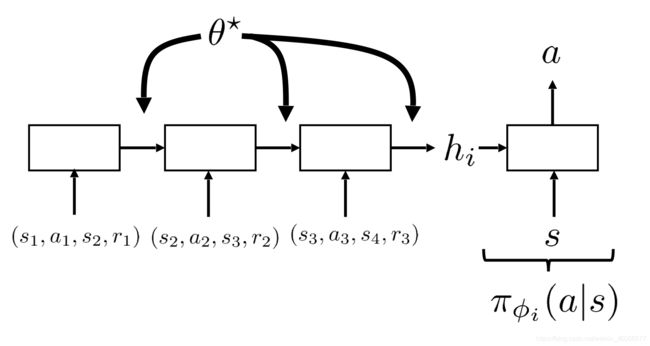

具体模型的输入,图上已经很清楚了,值得注意的是:
- 同一任务的不同Episode之间的信息都通过一个hidden state传递的
- 不同任务之间同使用一个RNN进行任务信息的存储
- 评价的指标是调整 θ \theta θ,使得多个任务在用专家数据Adapted出来的Policy的累积Reward最大,即 θ ∗ = arg max θ E π ϕ i ( τ ) [ r ( τ ) ] \theta^*=\argmax_\theta E_{\pi_{\phi_i}(\tau)}[r(\tau)] θ∗=θargmaxEπϕi(τ)[r(τ)]
要注意的是,从始至终我们要调整的都是RNN中的参数 θ \theta θ,而没有变动过关于问题的模型 ϕ \phi ϕ,只是利用它作为一个中间的桥梁对Meta Parameters即 θ \theta θ进行更新。
还是得说明一下:
- 对于一个task i i i,一开始 D i D_i Di中就放着任务 i i i真实数据,进行Adapt,可以进行几次,得一个Adapted Policy π h t \pi_{h_t} πht,即Adaptation Inner Loop
- 然后通过计算Adapted Policy即 π h \pi_h πh与专家数据 D i D_i Di之间的loss来调整 θ \theta θ,即Meta-Training Outer Loop
2.3 Optimization-Based( f f f为PG, L L L为PG)

顾名思义,选择RL的基本算法PG来做Adaptation,即 f f f,但好像有点模糊?
再次回顾一下Standard RL:
θ ∗ = arg max θ E π θ ( τ ) [ r ( τ ) ] ⏟ J ( θ ) P G : θ k + 1 = θ k + α ∇ θ k J ( θ k ) \theta^*=\argmax_\theta \underbrace{E_{\pi_\theta(\tau)}\Big[r(\tau)\Big]}_{J(\theta)}\\ PG:\theta^{k+1}=\theta^{k}+\alpha\nabla_{\theta^k}J(\theta^k) θ∗=θargmaxJ(θ) Eπθ(τ)[r(τ)]PG:θk+1=θk+α∇θkJ(θk)
于是有
ϕ i = f θ ( M i ) = θ + α ∇ θ J i ( θ ) = θ + α ∇ θ E π θ ( τ i ) [ r ( τ i ) ] \begin{aligned} \phi_i&=f_\theta(M_i)\\ &=\theta+\alpha \nabla_\theta J_i(\theta)\\ &=\theta +\alpha \nabla_\theta E_{\pi_\theta(\tau_i)}\Big[r(\tau_i)\Big] \end{aligned} ϕi=fθ(Mi)=θ+α∇θJi(θ)=θ+α∇θEπθ(τi)[r(τi)]
这是选择了 f f f为PG,即Adaptation后的参数 ϕ i \phi_i ϕi,然后有:
θ ← θ + α ∇ θ E π ϕ i ( τ ) [ r ( τ ) ] \theta\leftarrow \theta + \alpha \nabla_\theta E_{\pi_{\phi_i}(\tau)}\Big[r(\tau)\Big] θ←θ+α∇θEπϕi(τ)[r(τ)]
ϕ i ← θ + α ∇ θ E π θ ( τ i ) [ r ( τ i ) ] \phi_i\leftarrow \theta+\alpha\nabla_\theta E_{\pi_\theta(\tau_i)}\Big[r(\tau_i)\Big] ϕi←θ+α∇θEπθ(τi)[r(τi)]
因此最终形式为:
θ ← θ + α ∇ θ J i ( θ + α ∇ θ J i ( θ ) ) \theta\leftarrow \theta+\alpha\nabla_\theta J_i(\theta+\alpha\nabla_\theta J_i(\theta)) θ←θ+α∇θJi(θ+α∇θJi(θ))
具体算法流程:

Adaptation Inner Loop:
- 先用任务 i i i的真实数据 D i D_i Di进行Adapt,得到Adapted parameters ϕ i = θ − α ∇ θ L i ( π θ , D i ) \phi_i=\theta-\alpha\nabla_\theta L_i(\pi_\theta,D_i) ϕi=θ−α∇θLi(πθ,Di)
- 然后利用Adapted的Policy即 π ϕ \pi_\phi πϕ来收集Adapted的轨迹数据 D i ′ D_i' Di′
Meta-Training Outer Loop:
- 利用Adapted Policy得到的轨迹 D i ′ D_i' Di′与 π ϕ i \pi_{\phi_i} πϕi根据PG来计算 θ \theta θ
值得注意的是这里的 D i D_i Di与 D i ′ D_i' Di′就是用来估计下面的期望的:
D i ′ : θ ← θ + α ∇ θ E π ϕ i ( τ ) [ r ( τ ) ] D_i':\theta\leftarrow \theta + \alpha \nabla_\theta E_{\pi_{\phi_i}(\tau)}\Big[r(\tau)\Big] Di′:θ←θ+α∇θEπϕi(τ)[r(τ)]
D i : ϕ i ← θ + α ∇ θ E π θ ( τ i ) [ r ( τ i ) ] D_i:\phi_i\leftarrow \theta+\alpha\nabla_\theta E_{\pi_\theta(\tau_i)}\Big[r(\tau_i)\Big] Di:ϕi←θ+α∇θEπθ(τi)[r(τi)]
这就是鼎鼎大名的MAML,因为这里涉及到二阶导,因此有一些文章来改进这个,如:
- Foerster, Farquhar, Al-Shedivat, Rocktaschel, Xing, Whiteson. DiCE: The Infinitely Differentiable Monte Carlo Estimator.
- Rothfuss, Lee, Clavera, Asfour, Abbeel. ProMP: Proximal Meta-Policy Search.
这里有一个问题哦:
D i D_i Di与 D i ′ D_i' Di′的关系是什么?
D i ′ D_i' Di′是Adapted Policy与 M i M_i Mi环境交互得到的轨迹数据,进行PG更新这个很好理解。
D i D_i Di是任务 i i i真实数据,那是专家数据还是任务 i i i随机的真实数据?一开始随机的真实数据Adapt也能学习?好像有点奇怪呀,那看看下面的Meta-Imitation Learning吧~
2.4 Meta-Imitation Learning
2.4.1 f f f为Behavior Cloning, L L L为PG
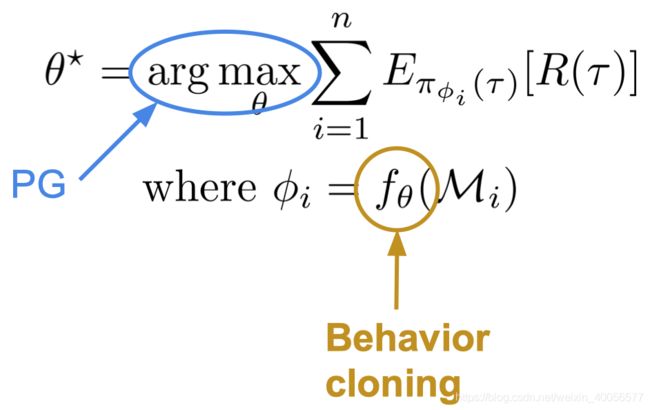 这里的 D i D_i Di就是利用真实的专家数据进行Adapt了,于是有:
这里的 D i D_i Di就是利用真实的专家数据进行Adapt了,于是有:
D i ′ : θ ← θ + α ∇ θ E π ϕ i ( τ ) [ r ( τ ) ] D_i':\theta\leftarrow \theta + \alpha \nabla_\theta E_{\pi_{\phi_i}(\tau)}\Big[r(\tau)\Big] Di′:θ←θ+α∇θEπϕi(τ)[r(τ)]
D i : ϕ i ← θ − α ∇ θ ∑ t ∣ ∣ π θ ( o t ) − a t ∗ ∣ ∣ 2 D_i:\phi_i\leftarrow \theta-\alpha\nabla_\theta \sum_t ||\pi_\theta(o_t)-a_t^*||^2 Di:ϕi←θ−α∇θt∑∣∣πθ(ot)−at∗∣∣2
Meta-Training的时候,由专家控制遥控器得到robot demos,即一个专家数据 τ = ( o 1 , a 1 , r 1 , . . . . , o T , a T , r T ) \tau=(o_1,a_1,r_1,....,o_T,a_T,r_T) τ=(o1,a1,r1,....,oT,aT,rT),可以看作 D i D_i Di
然后Meta-Training的时候,根据上面两个公式迭代,得到参数 θ \theta θ.
然后Meta-Test的时候,给定一条新的专家示意的数据 τ n e w \tau_{new} τnew,即 D i D_i Di,首先:
- Adaptation : D i : ϕ i ← θ − α ∇ θ ∑ t ∣ ∣ π θ ( o t ) − a t ∗ ∣ ∣ 2 D_i:\phi_i\leftarrow \theta-\alpha\nabla_\theta \sum_t ||\pi_\theta(o_t)-a_t^*||^2 Di:ϕi←θ−α∇θt∑∣∣πθ(ot)−at∗∣∣2
- 直接用Adapted的Policy即 π ϕ i \pi_{\phi_i} πϕi作为最终控制robot的控制器~
2.4.2 f f f为Learned loss, L L L为PG

这里将Adaptation Rule设定为Learned loss,因为在Behavior Cloning中搜集数据的方式是人为用遥控器控制的,于是轨迹样本robot demos是 τ = ( o 1 , a 1 , r 1 , . . . . , o T , a T , r T ) \tau=(o_1,a_1,r_1,....,o_T,a_T,r_T) τ=(o1,a1,r1,....,oT,aT,rT)。而在现在这个设定下,希望输入一个human demos而不是robot demos,然后robot就学会这个动作,而不是输入一个用遥控器控制的robot demos,具体区别如下:
于是在Meta-Training的时候,要将human demos与robot demos配对起来,即拍一个人操作的video与操纵遥控器的轨迹序列配对起来,训练Learned Cost,即:
ϕ = θ − α ∇ θ L ψ ( θ , d h ) \phi=\theta-\alpha\nabla_\theta L_\psi(\theta,d^h) ϕ=θ−α∇θLψ(θ,dh)
2.5 Meta-MBRL( f f f为SL with model, L L L为MPC)

关于Model-Based RL的算法概览可以参考Model-Based RL算法,主要分为Optimal Control进行Planning,不学习Policy的MBRL,学Policy的MBRL,此处简要回顾一下Without Policy的MBRL1.5
![]()
回顾一下:
- 随意跑一个base Polcy收集Transition 数据
- 然后通过Supervised Learning学习dynamics model,输入为 s , a s,a s,a,label为 s ′ s' s′
- 用一些planning算法如iLQR、MCTS来plan一下轨迹
- 执行plan的轨迹一些action,引入MPC使预测的轨迹稳定
- 将执行后获得的transition样本收集进行retrain
于是这里Adaptation Rule的应用对象 M i M_i Mi为dynamics model的参数 ϕ i \phi_i ϕi,然后根据Dynamics Model使用MPC算法来调整Meta-Parameters即 θ \theta θ。
为什么需要对Dynamics Model进行Adapt?
因为环境模型很容易就发生变化:
- 真实Agent电量不足,降低功率
- 平坦地面上训练的Agent,放到陡峭的地面上
- 使用过程中,Agent自身损耗,导致dynamics model发生变化等等
那high-level的流程是如何的呢?
原来的是这样的,学好一个model后,利用Controller进行plan。

现在引入了一个Update rule,需要Meta-Training的时候训练好,然后输入recent的几个transition ( s , a , s ′ ) (s,a,s') (s,a,s′)即图中的recent,Adapted出一个Model,再进行MPC算法
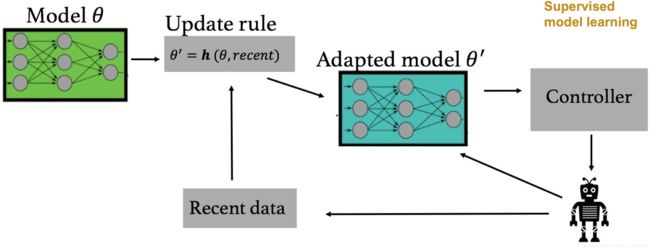
具体公式流程阐述如下:
此处用 d θ ( s , a ) = f θ ( s , a ) d_\theta(s,a)=f_\theta(s,a) dθ(s,a)=fθ(s,a)代表了一下,毕竟dynamics model

由公式可以看出, f f f为Supervised Learning的意思为MSE loss即 J ( θ ) = ∣ ∣ d θ ( s , a ) − s ′ ∣ ∣ 2 J(\theta)=||d_\theta(s,a)-s'||^2 J(θ)=∣∣dθ(s,a)−s′∣∣2, L L L为MPC的意思为第三步。
上面为Meta-Test的过程,以下为Meta-Training来训练 d θ ( s , a ) d_\theta(s,a) dθ(s,a)的过程:
-
记得第一小节的定义:
D t r = { D 1 t r , . . . , D n t r } , D t s = { D 1 t s , . . . , D n t s } , D m e t a − t r a i n = { D t r , D t s } D_{tr}=\{D_1^{tr},...,D_n^{tr}\},D_{ts}=\{D_1^{ts},...,D_n^{ts}\},D_{meta-train}=\{D^{tr},D^{ts}\} Dtr={D1tr,...,Dntr},Dts={D1ts,...,Dnts},Dmeta−train={Dtr,Dts}D i t r = { ( x 1 i , y 1 i ) , ⋯ , ( x k i , y k i ) } D i t s = { ( x 1 i , y 1 i ) , ⋯ , ( x l i , y l i ) } D_i^{tr}=\{(x_1^i,y_1^i),\cdots,(x_k^i,y_k^i)\}\\ D_i^{ts}=\{(x_1^i,y_1^i),\cdots,(x_l^i,y_l^i)\} Ditr={(x1i,y1i),⋯,(xki,yki)}Dits={(x1i,y1i),⋯,(xli,yli)}
-
Model的训练样本即transition为 ( s , a , s ′ ) (s,a,s') (s,a,s′),因此套上去为 x = ( s , a ) , y = ( s ′ ) x=(s,a),y=(s') x=(s,a),y=(s′)
-
从很多种不同的Dynamic中收集的Experience中进行Sample一条第I种类型Dynamics的Trajectory记为 τ i \tau_i τi(多条也ok)如下:
τ i = ( s t , a t , s t + 1 , a t + 1 , . . . , s t + k , a t + k , s t + k + 1 ) \tau_i=(s_t,a_t,s_{t+1},a_{t+1},...,s_{t+k},a_{t+k},s_{t+k+1}) τi=(st,at,st+1,at+1,...,st+k,at+k,st+k+1) -
从 τ \tau τ中获取 D i t r , D i t s D^{tr}_i,D_i^{ts} Ditr,Dits,如:
D i t r = { ( s t , a t , s t + 1 ) , . . . , ( s t + k − 1 , a t + k − 1 , s t + k ) } D i t s = { s t + k , a t + k , s t + k + 1 } D^{tr}_i=\{(s_t,a_t,s_{t+1}),...,(s_{t+k-1},a_{t+k-1},s_{t+k})\}\\ D_i^{ts}=\{s_{t+k},a_{t+k},s_{t+k+1}\} Ditr={(st,at,st+1),...,(st+k−1,at+k−1,st+k)}Dits={st+k,at+k,st+k+1}
这里选择了k个训练transitions, l = 1 l=1 l=1的测试样本,选多少自己决定。
2.6 Inference-Based ( f f f为Stochastic Encoder, L L L为SAC)
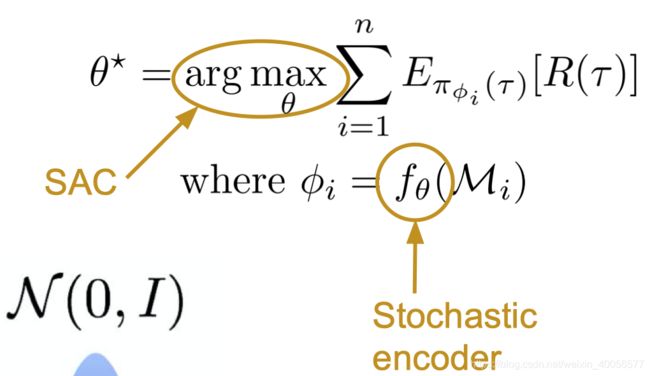
在详细解释 f θ f_\theta fθ选择为Stochastic Encoder与 L L L选择为SAC的情况时,先小总结一下Meta-RL,再说说POMDP以及SAC。
2.6.1 Meta-RL
再啰嗦一下Meta-RL的特性:步骤分为Meta-Training与Adaptation,即
θ ∗ = max θ ∑ i = 1 n l o g p ( ϕ i ∣ D i t s ) ϕ i = f θ ( D i t r ) \theta^*=\max_\theta \sum_{i=1}^nlogp(\phi_i|D_i^{ts})\\ \phi_i=f_\theta(D_i^{tr}) θ∗=θmaxi=1∑nlogp(ϕi∣Dits)ϕi=fθ(Ditr)
关键的一步是用 D i t r D_i^{tr} Ditr对元模模型参数 θ \theta θ进行Adaptation,但是没有办法evaluate,因此需要放到细分任务中用测试数据 D i t s D_i^{ts} Dits评价,从而调整Meta-Parameters.
因此元学习中的参数 θ \theta θ,尝试从多任务的经验数据中提取出共同的学习技巧或Knowledge,而每一个细分任务之间最大的不同是dynamics与reward,或者说在设计多任务的时候,一般都在同一环境中保持 s t , a t s_t,a_t st,at的空间相同,然后改变 p ( s ′ ∣ s , a ) , r p(s'|s,a),r p(s′∣s,a),r,因此Meta-RL的概率图可以简单描述如下: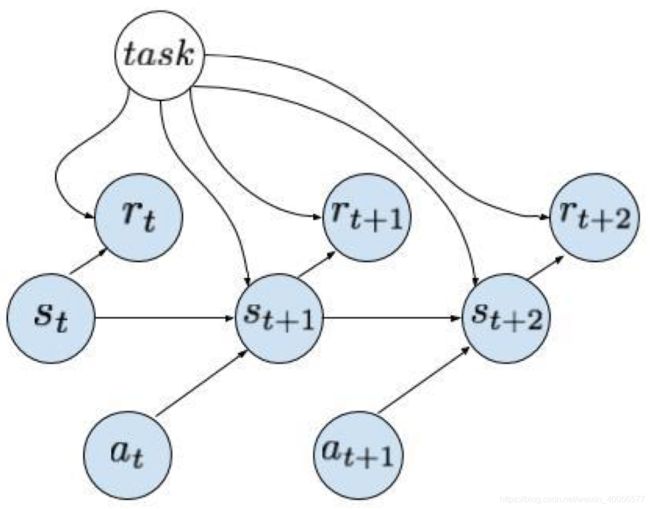
- 当前实际环境的dynamics模型 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a)与奖励 r t r_t rt,都conditon on task的信息
- 收集真实环境的一些数据 D i D_i Di,输入 f θ f_\theta fθ,得到task-specific的参数 ϕ i \phi_i ϕi
- 然后在 ϕ i \phi_i ϕi设定的任务框架下收集数据 D i ′ D_i' Di′,Meta-test通过 L ( ϕ i , D i ′ ) L(\phi_i,D_i') L(ϕi,Di′)将模型参数 ϕ i \phi_i ϕi调优,而Meta-Training时则把 θ \theta θ调优
2.6.2 POMDP
在Model-based RL中的Complex Observations中提过引入Latent Space的模型目标为:
max ϕ 1 N ∑ i = 1 N ∑ t = 1 T E ( s t , s t + 1 ) ∼ p ( s t , s t + 1 ∣ o 1 : T , a 1 : T ) [ l o g p ϕ ( s t + 1 i ∣ s t i , a t i ) + l o g p ϕ ( o t i ∣ s t i ) ] \max_{\phi}\frac{1}{N}\sum_{i=1}^N\sum_{t=1}^TE_{(s_t,s_{t+1})\sim p(s_t,s_{t+1}|o_{1:T},a_{1:T})}\Big[logp_\phi(s_{t+1}^i|s_t^i,a_t^i)+logp_\phi(o_t^i|s_t^i)\Big] ϕmaxN1i=1∑Nt=1∑TE(st,st+1)∼p(st,st+1∣o1:T,a1:T)[logpϕ(st+1i∣sti,ati)+logpϕ(oti∣sti)]
然后处理Encoder的时候假设了最简单的情形:
- 独立性假设 p ( s t , s t + 1 ∣ o 1 : T , a 1 : T ) = p ( s t ∣ o 1 : T , a 1 : T ) p ( s t + 1 ∣ o 1 : T , a 1 : T ) p(s_t,s_{t+1}|o_{1:T},a_{1:T})=p(s_t|o_{1:T},a_{1:T})p(s_{t+1}|o_{1:T},a_{1:T}) p(st,st+1∣o1:T,a1:T)=p(st∣o1:T,a1:T)p(st+1∣o1:T,a1:T)
- 学习一个 q ψ ( s t ∣ o 1 : T , a 1 : T ) q_\psi(s_t|o_{1:T},a_{1:T}) qψ(st∣o1:T,a1:T)来近似这个分布 p ( s t ∣ o 1 : T , a 1 : T ) p(s_t|o_{1:T},a_{1:T}) p(st∣o1:T,a1:T)
- 假设 s t s_t st只condition on o t o_t ot,即 q ψ ( s t ∣ o t ) q_\psi(s_t|o_t) qψ(st∣ot)
- q ψ ( s t ∣ o t ) q_\psi(s_t|o_t) qψ(st∣ot)是deterministic encoder,即等价于让 s t = g ψ ( o t ) s_t=g_\psi(o_t) st=gψ(ot)
于是优化目标变为:
max ϕ , ψ 1 N ∑ i = 1 N ∑ t = 1 T [ l o g p ϕ ( g ψ ( o t i ) ∣ g ψ ( o t i ) , a t i ) + l o g p ϕ ( o t i ∣ g ψ ( o t i ) ) ] \max_{\phi,\psi}\frac{1}{N}\sum_{i=1}^N\sum_{t=1}^T\Big[logp_\phi\Big(g_\psi(o_t^i)|g_\psi(o_t^i),a_t^i\Big)+logp_\phi(o_t^i|g_\psi(o_t^i))\Big] ϕ,ψmaxN1i=1∑Nt=1∑T[logpϕ(gψ(oti)∣gψ(oti),ati)+logpϕ(oti∣gψ(oti))]
POMDP就是指的incomplete information,复杂的observation,unknow state,因此如果要使用Meta-Lerning的想法,加入任务信息,其概率图如下:

在假设中,Encoder即 q ψ ( s t ∣ o t ) q_\psi(s_t|o_t) qψ(st∣ot)被假设成了deterministic,从而被转换成 g ψ ( o t ) = s t g_\psi(o_t)=s_t gψ(ot)=st,而Stochastic Encoder的意思是 q ψ ( s t ∣ o t ) q_\psi(s_t|o_t) qψ(st∣ot)是一个概率分布,一个observation可能被encode into多个可能的states。
而且还可以继续放松假设,如 q ψ ( s t ∣ o t ) → q ψ ( s t ∣ o 1 : T ) q_\psi(s_t|o_t)\rightarrow q_\psi(s_t|o_{1:T}) qψ(st∣ot)→qψ(st∣o1:T)
2.6.3 SAC
先High-Level的总结一下:
- Soft实际的意思是指加了一个Entropy term的Objective,即 J ( π ) = ∑ t = 0 T E s t ∼ p ( s t ) , a ∼ π ( a t ∣ s t ) [ r ( s t , a t ) + α H [ π ( • ∣ s t ) ] ] J(\pi)=\sum_{t=0}^TE_{s_t\sim p(s_t),a\sim \pi(a_t|s_t)}\Big[r(s_t,a_t)+\alpha H[\pi(•|s_t)]\Big] J(π)=t=0∑TEst∼p(st),a∼π(at∣st)[r(st,at)+αH[π(•∣st)]]
- 对Actor与Critic同时建模,对policy用参数 θ \theta θ(Actor),对Q-Value用参数 ϕ \phi ϕ(Critic)建模表示
C r i t i c : J Q ( ϕ ) = E ( s t , a t ) ∼ D [ 1 2 ( Q ϕ ( s t , a t ) − Q ^ ( s t , a t ) ) 2 ] Critic:\quad J_Q(\phi)=E_{(s_t,a_t)\sim D}\Big[\frac{1}{2} \Big(Q_\phi(s_t,a_t)-\hat Q(s_t,a_t)\Big)^2\Big] Critic:JQ(ϕ)=E(st,at)∼D[21(Qϕ(st,at)−Q^(st,at))2]
A c t o r : J π ( θ ) = E s t , a t [ Q ϕ ( s t , a t ) + α H [ π θ ( • ∣ s t ) ] ] Actor:\quad J_\pi(\theta)=E_{s_t,a_t}\Big[Q_\phi(s_t,a_t)+\alpha H\big[\pi_\theta(•|s_t)\big]\Big] Actor:Jπ(θ)=Est,at[Qϕ(st,at)+αH[πθ(•∣st)]]
然后从Replay Buffer从用Importance Sampling之类的来采样,更新AC,如下图所示:
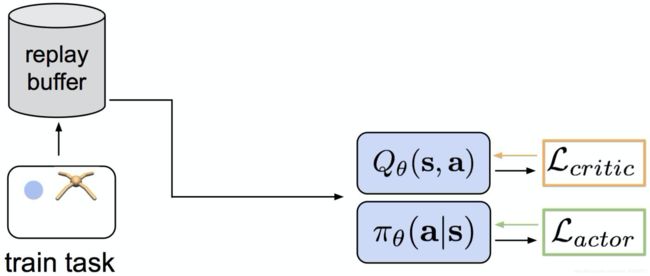
更详细的具体算法在这篇Soft Optimality Framework中贴了一下OpenAI的算法流程图如下:

2.6.4 Inference-Based Method

Inference-Based Method就是在POMDP的语境下的第三类做法,由上图可知,把高维度的Observation Encode成hidden state h t h_t ht,而这个hidden state包含 ( s t , t a s k ) (s_t,task) (st,task),训练好后,便可由Observation推断(Inference)出state以及task information(记为 z z z)。
直接抛出 f f f为Stochastic Encoder, L L L为SAC的如下流程图:

Meta-Learning的两个流程:
- Meta-Training Outer Loop:
θ ∗ = arg max θ E π ϕ i ( τ ) [ r ( τ ) ] \theta^*=\argmax_\theta E_{\pi_{\phi_i}(\tau)}[r(\tau)] θ∗=θargmaxEπϕi(τ)[r(τ)] - Adaptation Inner Loop
ϕ i = f θ ( M i ) \phi_i=f_\theta(M_i) ϕi=fθ(Mi)
- 将多任务 M 1 , . . . , M n M_1,...,M_n M1,...,Mn 通过一个Stochastic Encoder 成 一个Task Embedding Vector z z z,需要设定Task Distribution,即 p ( z ) p(z) p(z)
- 然后这个Task Distribution的Parameters,即为 ϕ \phi ϕ,也叫Adapted Parameters
- 这里的 θ \theta θ是Meta-Parameters,主要是Policy与Q-Function中的参数,即Actor-Critic中的参数
三、总结
| Meta算法 | f f f | L L L |
|---|---|---|
| Recurrence-Based | RNN | PG |
| Optimization-Based | PG | PG |
| Inference-Based | Stochastic Encoder | SAC |
| Meta-MBRL | SL | MPC |
| Meta-IL-1 | Behavior Cloning | PG |
| Meta-IL-2 | Learned Loss | PG |
后记
本来还是打算写在CV中的Meta-Learning,但发现光写Meta-RL就够呛。
主要参考资料是CS285 PPT Lec20 由Kate Rakelly讲授
还有ConfTube上的 ICML 2019 Meta-Learning Tutorial
后面还有关于Exploration与Exploitation的一篇总结性博文
以及三个Courses:
- Convex Duality in RL
- Rethinking RL from the perspective of Generalization(Chelsea Finn)
- Multi-task RL:A curse or a blessing?