机器学习——朴素贝叶斯算法Python实现

简介

这里参考《统计学习方法》李航编进行学习总结。详细算法介绍参见书籍，这里只说明关键内容。


即

条件独立下：p{X=x|Y=y}=p{X1=x1|Y=y} * p{X2=x2|Y=y} *...* p{Xn=xn|Y=y}

（4.4）等价于p{Y=ck|X=x}= p{X=x|Y=ck}*p{Y=ck} / p{X=x}
所以对不同的Y=ck，分母都是一样的，最后（4.7）比较选出最大概率时可以忽略分母，仅比较分子。
而分子为p{Y=ck} * p{X1=x1|Y=ck}* p{X2=x2|Y=ck}*…*p{Xn=xn|Y=ck}

所以（4.7）的公式即为
max(p{Y=ck}* p{X1=x1|Y=ck} * p{X2=x2|Y=ck}*…*p{Xn=xn|Y=ck}) (k=1,2,…) 并返回对应的ck。

因此模型只需要训练出（生成）所有的 p{Y=ck} 和 p{Xi=xij|Y=ck}就可以利用（4.7）进行分类了.
(注：这里的xij表示第i个特征的第j个取值。）

案例：

下面通过一个实例来实现这个算法。
项目数据下载及说明，如下链接：
http://archive.ics.uci.edu/ml/datasets/Car+Evaluation
请自行下载数据，以及了解数据的相关内容。

数据样例：

Class Values:
unacc, acc, good, vgood

Attributes:
buying: vhigh, high, med, low.
maint: vhigh, high, med, low.
doors: 2, 3, 4, 5more.
persons: 2, 4, more.
lug_boot: small, med, big.
safety: low, med, high.

样本：

vhigh,vhigh,2,2,small,low,unacc
vhigh,vhigh,2,2,small,med,unacc
vhigh,vhigh,2,2,small,high,unacc
vhigh,vhigh,2,2,med,low,unacc
vhigh,vhigh,2,2,med,med,unacc
vhigh,vhigh,2,2,med,high,unacc
,,,
…
…

先读取数据：

import numpy as np

#从文档中读取数据，每条数据转成列表的形式
def readData(path):
    dataList = []
    with open(path,'r') as f:
        dataSet = f.readlines()

    for d in dataSet:
        d = d[:-1]
        d = d.split(',')
        print(d)
        dataList.append(d)

    return dataList

然后利用这些数据生成所有的 p{Y=ck} 和 p{Xi=xij|Y=ck}。

#为方便代码处理，先做属性映射
#分类值映射
Cls = {'unacc':0, 'acc':1, 'good':2, 'vgood':3}   
#特征值映射，共6个特征值，每个特征表示为X[i]，X[i][xiv]表示特征Xi的取值。
X = [{'vhigh':0, 'high':1, 'med':2, 'low':3},
         {'vhigh':0, 'high':1, 'med':2, 'low':3},
         {'2':0, '3':1, '4':2, '5more':3},
         {'2':0, '4':1, 'more':2},
         {'small':0, 'med':1, 'big':2},
         {'low':0, 'med':1, 'high':2}]

#训练模型，生成概率矩阵即生成p{Y=yi}和 p{Xi=xij|Y=yi}
def NBtrain(labelData):
    datanum = len(labelData)

    Arr = np.zeros((4,6,4))   #Arr[y][xi][xiv]表示在分类y的条件下，特征Xi取值为xiv的数量。
    for d in labelData:
        y = Cls[d[-1]]     #取分类的映射值
        for i in range(len(d)-1):
            v = X[i][d[i]]    #取每个特征的映射值
            Arr[y][i][v] +=1  #计数

    probXCY = np.zeros((4,6,4))  #probXCY[y][xi][xiv]表示在分类y的条件下，特征Xi取值为xiv的概率即p{Xi=xiv|Y=y}
    numY = []         #分类为yi的数量
    probY =[]         #分类为yi的概率

    for y in Cls.values():
        numY.append(np.sum(Arr[y][0]))
        probY.append( numY[y]/datanum ) 
        print(y, numY[y], probY[y])
        for xi in range(len(X)):
            s = len(X[xi])    #特征Xi的值的个数。
            for xiv in X[xi].values():
                probXCY[y][xi][xiv] = Arr[y][xi][xiv]/numY[y] 
            print('\n')

    # print(Arr)
    # print(probXCY)
    return probXCY,probY

训练模型生成后就需要完成对新数据的分类任务，其实就是实现（4.7）的计算就可以了。实现代码如下：

def NBclassify(probXCY,probY,predData):
    unknowData = predData
    datanum = len(unknowData)
    YofX = []    #记录数据的分类
    diffNum = 0  #记录分类结果与实际不同的数量
    for d in unknowData:
        probyCx = []    #记录p{Y=yi|X[...]=x[...]}
        for y in Cls.values():
            p = 10**5   #概率偏移，防止计算得到的数值过小
            for xi in range(len(X)):
                xiv = X[xi][d[xi]]    #取映射值
                p *= probXCY[y][xi][xiv]
            p *= probY[y]    #p =p{y} * p{X1=x1|Y=y} * p{X2=x2|Y=y} *...* p{Xn=xn|Y=y} 
            probyCx.append(p)

        YofX.append(probyCx.index(max(probyCx)))  #等同于max( p{Y=yi|X=x} )即取概率最大的那个分类yi为该数据的分类

        print(d)
        print("分类为：",YofX[-1])
        if(YofX[-1] != Cls[d[-1]]):
            diffNum +=1
            #print(probyCx)
            print("真实分类为：",Cls[d[-1]])
        else:
            print("分类正确")


    print("错误数：",diffNum,"\t数据量:",datanum)
    print("错误率：",diffNum/datanum)

    return YofX

至此就完成了案例的朴素贝叶斯分类的实现，你可以将数据分成两部分，一部分用于训练，一部分用于测试。也可以直接将整个数据作为训练同时用于测试。

上述算法存在些小问题，会出现概率值为0 的情况


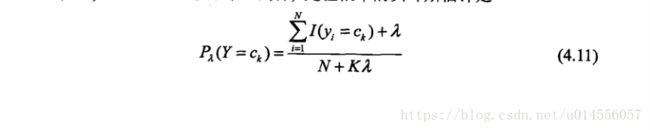
为了避免概率值为零的情况采用拉普拉斯平滑做调整。训练函数对应于这两个公式的两条语句做点修改。如下：

probY.append( (numY[y]+1)/(datanum+len(Cls)) )  #做拉普拉斯平滑

s = len(X[xi])    #特征Xi的值的个数。            
probXCY[y][xi][xiv] = (Arr[y][xi][xiv]+1)/(numY[y]+s)   #做拉普拉斯平滑避免概率值为0的情况

下面是完整代码：

import numpy as np
from enum import Enum

#从文档中读取数据，每条数据转成列表的形式
def readData(path):
    dataList = []
    with open(path,'r') as f:
        dataSet = f.readlines()

    for d in dataSet:
        d = d[:-1]
        d = d.split(',')
        print(d)
        dataList.append(d)

    return dataList

# http://archive.ics.uci.edu/ml/datasets/Car+Evaluation
# Class Values:
# unacc, acc, good, vgood
#
# Attributes:
# buying: vhigh, high, med, low.
# maint: vhigh, high, med, low.
# doors: 2, 3, 4, 5more.
# persons: 2, 4, more.
# lug_boot: small, med, big.
# safety: low, med, high.

#映射属性值，方便代码处理
Cls = {'unacc':0, 'acc':1, 'good':2, 'vgood':3}   #分类值映射
#特征值映射，共6个特征值，每个特征表示为X[i]，X[i][xiv]表示特征Xi的取值。
X = [{'vhigh':0, 'high':1, 'med':2, 'low':3},
         {'vhigh':0, 'high':1, 'med':2, 'low':3},
         {'2':0, '3':1, '4':2, '5more':3},
         {'2':0, '4':1, 'more':2},
         {'small':0, 'med':1, 'big':2},
         {'low':0, 'med':1, 'high':2}]

#训练模型，生成概率矩阵即生成p{Y=yi}和 p{Xi=xiv|Y=yi}
def NBtrain(labelData):
    datanum = len(labelData)

    Arr = np.zeros((4,6,4))   #Arr[y][xi][xiv]表示在分类y的条件下，特征Xi取值为xiv的数量。
    for d in labelData:
        y = Cls[d[-1]]     #取分类的映射值
        for i in range(len(d)-1):
            v = X[i][d[i]]    #取每个特征的映射值
            Arr[y][i][v] +=1  #计数

    probXCY = np.zeros((4,6,4))  #probXCY[y][xi][xiv]表示在分类y的条件下，特征Xi取值为xiv的概率即p{Xi=xiv|Y=y}
    numY = []         #分类为yi的数量
    probY =[]         #分类为yi的概率

    for y in Cls.values():
        numY.append(np.sum(Arr[y][0]))
        probY.append( (numY[y]+1)/(datanum+len(Cls)) )  #做拉普拉斯平滑
        print(y, numY[y], probY[y])
        for xi in range(len(X)):
            s = len(X[xi])    #特征Xi的值的个数。
            for xiv in X[xi].values():
                probXCY[y][xi][xiv] = (Arr[y][xi][xiv]+1)/(numY[y]+s)   #做拉普拉斯平滑避免概率值为0的情况

[3]/numY[0])

    # print(Arr)
    # print(probXCY)
    return probXCY,probY


def NBclassify(probXCY,probY,predData):
    unknowData = predData
    datanum = len(unknowData)
    YofX = []    #记录数据的分类
    diffNum = 0  #记录分类结果与实际不同的数量
    for d in unknowData:
        probyCx = []    #记录p{Y=yi|X[...]=x[...]}
        for y in Cls.values():
            p = 10**5   #概率偏移，防止计算得到的数值过小
            for xi in range(len(X)):
                xiv = X[xi][d[xi]]    #取映射值
                p *= probXCY[y][xi][xiv]
            p *= probY[y]    # p{X1=x1|Y=y} * p{X2=x2|Y=y} *...* p{Xn=xn|Y=y} * p{y}
            probyCx.append(p)

        YofX.append(probyCx.index(max(probyCx)))  #max( p{Y=yi|X[...]=x[...]} )即取概率最大的那个分类yi为该数据的分类

        #分类记录
        print(d)
        print("分类为：",YofX[-1])
        if(YofX[-1] != Cls[d[-1]]):
            diffNum +=1
            #print(probyCx)
            print("真实分类为：",Cls[d[-1]])
        else:
            print("分类正确")


    print("错误数：",diffNum,"\t数据量:",datanum)
    print("错误率：",diffNum/datanum)

    return YofX

#测试：
dS = readData('car.data.txt')
probXCY,probY = NBtrain(dS)
NBclassify(probXCY,probY,dS)

运行输出结果为：

...
...
...
['low', 'low', '5more', 'more', 'big', 'med', 'good']
分类为： 2
分类正确
['low', 'low', '5more', 'more', 'big', 'high', 'vgood']
分类为： 3
分类正确
错误数： 223    数据量: 1728
错误率： 0.12905092592592593