备战数学建模21-马尔可夫算法
目录
一、随机过程与马尔可夫链(马氏链)定义
1-随机过程与马尔可夫链相关概念
2-马尔可夫链的两个重要类型
二、马氏链模型案例
1-健康与疾病
2-钢琴销售的存储策略
3-疫苗成效的预测
一、随机过程与马尔可夫链(马氏链)定义
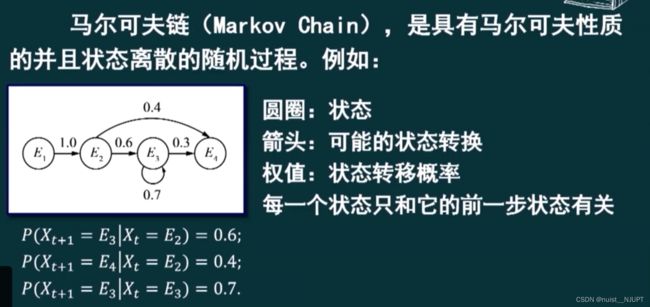
1-随机过程与马尔可夫链相关概念
我们看个例子1,这个随机抽取的过程可理解为随机过程,状态空间就0和1两种。
我们再看例子2,其实就是把实际问题抽象成数学语言的一个方法。
看一下马尔可夫链的时齐性:
我们看例子3,一共4种空间状态, 记录不同时刻不同的空间状态如下所示:
我们可以得到转移概率矩阵如下:
2-马尔可夫链的两个重要类型
上述求转移概率矩阵的MATLAB代码如下所示:
clear; clc
format rat;%使用分数来表示值
a=[4 3 2 1 4 3 1 1 2 3
2 1 2 3 4 4 3 3 1 1
1 3 3 2 1 2 2 2 4 4
2 3 2 3 1 1 2 4 3 1];
a=a';
a=a(:)';
for i=1:4
for j=1:4
f(i,j)=length(findstr([i,j],a));%统计字符串ij的数量
end
end
ni=sum(f,2);%按照行求和
phat=f./repmat(ni,1,size(f,2));%矩阵除法
disp(phat);
format %恢复到短小数的表示形式
二、马氏链模型案例
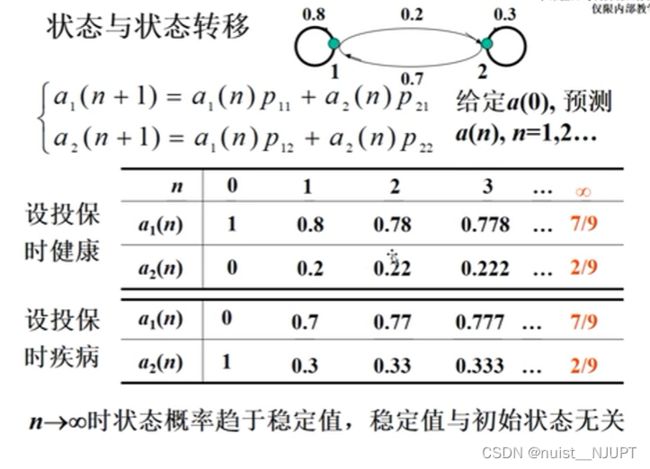
1-健康与疾病
根据题目意思,我们发现Pij的值,P11=0.8,P12=0.2,P21=0.7,P22=0.3.
由于当前状态只取决于前一个状态与转移矩阵,故可以写出转移状态概率方程。
上述例子1的MATLAB代码实现:
clear; clc
format rat;%使用分数来表示值
a = [1, 0] ;
p = [0.8, 0.2; 0.7, 0.3] ;
for i = 1 : 1000
a = a * p ;
end
disp(a) ;2-钢琴销售的存储策略
我们简单分析一下如下的钢琴销售和存储问题,按经验估计每周需要一架钢琴,仅当库存为0时,才购买3架钢琴,思考在这种情况下,失去销售机会(即供不应求)的概率,同时求出每周的平均销售量为多少?
假设Dn为第n周钢琴的需求量,需求量服从泊松分布,可以得出需求量的概率。我们可以写出状态转移矩阵P,从库存1到1,概率为0.368,其余依次类推。写出一个3*3的概率转移矩阵。
根据马尔可夫正则链的规则,建立wP = w的方程,这样可以求出w1,w2,w3.
根据公式求出第n周失去销售机会的概率,具体如下:
3-疫苗成效的预测
通过统计注射疫苗的人的月度平均成效,其值越高,说明成效越好,成效值在0到12之间。
下面给出国内和国外的疫苗两组数据,分别为15-17年疫苗的平均成效,具体如下:
使用马尔可夫链进行预测疫苗成效具体分为四步:
第一步,将成效划分成6个等级状态,等级越高的成效越好;
第二步,求出状态转移频数矩阵和状态转移概率矩阵;
第三步, 预测后阶段的状态概率,预测状态概率最大的为预测状态;
第四步,对比预测状态的中值和实际值,评价预测效果。
我们首先将国内疫苗成效表写成成效等级的形式,具体如所示:
我们根据疫苗成效等级表,我们可以计算出状态频数矩阵和状态概率矩阵, 设置初始
因为17年12月份的状态为E5,故我们设置初始概率矩阵A = [0,0,0,0,1,0] ; 这样我们就可以对18年1-6月的成效数据进行预测了,通过上述,可以计算出18年的状态概率矩阵,其中概率最大的状态即为预测状态,根据预测国产疫苗在7月份预测效果较好。
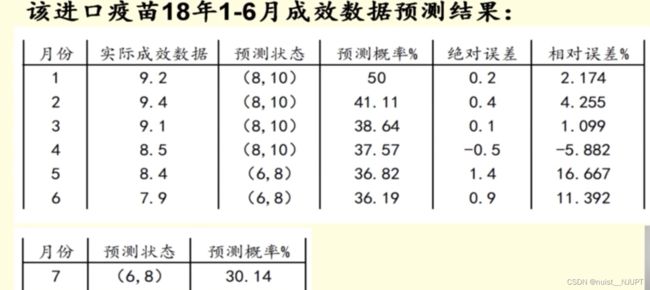
同样的方法对进口疫苗进行预测,预测结果如下所示:
上述使用马尔可夫链进行预测的MATLAB代码如下所示:
clear; clc
a=[4 1 0 0 0 0
1 2 2 1 0 0
0 1 2 2 1 0
0 0 2 2 2 1
0 1 0 1 3 0
0 1 0 0 0 6];
ni = sum(a,2);%按照行求和
p = a./repmat(ni,1,size(a,2));%矩阵除法
disp('转移概率矩阵如下:') ;
disp(p); %求出状态转移概率矩阵
e = [0,0,0,0,1,0] ; %初始概率序列
disp('1-7月份的预测概率序列如下:') ;
for i = 1 : 7
e= e * p ;
[m, index] = max(e) ;
p1 = m / sum(e) ; %预测概率
disp(['第',num2str(i), '个月预测国产疫苗等级 = ', num2str(index), ',预测概率 = ', num2str(p1)]) ;
% disp(index) ;
end
%绝对误差 = 真实值 - 预测值 ; 相对误差 = 绝对误差 / 真实值 ;
a1 = [3 2 0 0 0 0
1 2 1 0 1 0
1 1 2 2 0 0
0 0 3 2 1 0
0 0 0 2 4 0
0 0 0 0 1 6] ;
ni1 = sum(a1,2);%按照行求和
ps = a1./repmat(ni1,1,size(a1,2));%矩阵除法
disp('转移概率矩阵如下:') ;
disp(ps); %求出状态转移概率矩阵
e = [0,0,0,0,1,0] ; %初始概率序列
disp('1-7月份的预测概率序列如下:') ;
for i = 1 : 7
e= e * ps ;
[m, index] = max(e) ;
p1 = m / sum(e,2) ; %预测概率
disp(['第',num2str(i), '个月预测进口疫苗等级 = ', num2str(index), ',预测概率 = ', num2str(p1)]) ;
% disp(index) ;
end
最后总结一下:马尔科夫链模型作为预测工具,可以用来预测例如商品价格等满足已知当前状态情况下,过去时间和未来相互独立的数据。