OTFS白皮书-翻译
OTFS白皮书-翻译
- 译者前言
- 正文
-
- 摘要
- 1. OTFS – 一种次世代调制方法
- 2. OTFS原理
-
- 2.1 OTFS简述
- 2.2 延迟-多普勒的信号表示方式
- 2.3 信号处理的整体框架
- 待续... ...
- 引用
译者前言
原著OTFS: A New Generation of Modulation Addressing the Challenges of 5G,
作者Ronny Hadani, Anton Monk, Cohere Technologies,
仅用于学习目的,请勿用作他用。
我不确定该怎么翻译的时候会用(?)标注。
正文
摘要
本论文介绍了一种名为OTFS(Orthogonal Time Frequency Space-正交时频空)的二维调制方法。OTFS使用延迟-多普勒域上的新一类载波实现QAM符号的多路传输。OTFS找到了传统时域调制(TDM)和频域调制(FDM)的共通之处,更广义地讲,OTFS将雷达领域和通信领域的技术结合了起来。OTFS波形受无线信道影响发生的变化能直接体现出物理环境的状况,从而可以由之推导出传输环境中会反射无线信号的反射体的高解析度雷达图。因此,原本具有时域及频域选择性的信道可以被转化为一个时不变(?)、频不变(?)(总之是不变的、静态的?)、可分并且正交的对无线信号的“影响”。所有的QAM符号都将受到由相同位置因素(?)决定的衰减,而所有延迟-多普勒分集产生的不同的信号版本都可以相干地结合起来。通过将不同反射物在延迟-多普勒域精确地分离开,并且根据MIMO的秩对频谱利用率(?)进行线性调整,OTFS可以在实现性能与复杂度的最优化取舍的情况下,使传输速率接近信道容量,并有效抵御多普勒效应与多径效应产生的负面影响。即使是在充满挑战性的、极端苛刻的5G通信环境下,OTFS仍能使MU-MIMO的增益能够被最大化利用。
1. OTFS – 一种次世代调制方法
历史教导我们:每当无线通信所需的空口遇到瓶颈,我们就需要研发新一代无线通信技术来满足增长的需求:从基于单载波GSM的2G无线通信网开始,到基于CDMA(码分复用)的3G无线通信网,再到如今的基于OFDM(正交频分复用)的4G网络。当已有的技术在性能、容量或成本方面无法满足需求时,我们就需要引入新的空口。比如说,当3G的CDMA因为抵抗信号干扰的能力有限而无法满足增长的数据传输速度需求时,基于窄带OFDM并且能够更有效利用带宽的4G技术便应运而生。
当前的5G网络需要满足非常多样的应用场景的需求,如【1】中所述。Multi-user MIMO是基本需求之一,这意味着当基站使用大量天线器件时,移动宽带频谱使用效率必须有飞跃性的提升,同时还需要有先进的预编码技术协同。使用传统OFDM技术的话,即使使用非常复杂的结构(什么的结构?),实际上也无法达到理论信道容量,并且还会由于频域时域选择性【2】【3】产生性能劣化。在其他重要5G应用场景中,比如V2V和高铁这类信道变化极快的场景中,根据信道状况做出调整来进行优化传输是不现实的,此时4G的OFDM窄带通信就显得很无用。因此,我们必须在找到更符合场景的空口和在信道变化极快的情况下调整优化的这两者中做出抉择:
既然解决在信道变化极快的情况下调整优化这一问题不现实,那我们就解决造成调整优化需求的原因。
这么做的前提是不牺牲性能。而这需要将两条冲突的原则结合:其一,扩频原则(如CDMA中所用),从而获取对窄带通信中的干扰的抵抗力以及充分利用在信道条件无法预测时的信道分集增益;其二,正交原则(如OFDM技术所用),从而简化信道耦合,并在不在提高复杂度的同时提升性能与频谱利用效率。
在OTFS调制中,承载信息的QAM符号被调制到被同时扩频(?)到时域与频域的波形上。这些波形在通过一般的有延迟-多普勒衰减的信号后相互间仍能保持粗略的正交性。OTFS波形的关键特性在于,它们是根据无线信号反射物对无线信号的影响做了最优化应对的。无线信道响应与承载了信息的QAM符号间简单而对称(?)地相互影响会促进最优化兼顾性能与复杂度的发送器和接收器的设计。总之,OTFS将扩频的可靠性以及鲁棒性与窄带通信的高频谱利用率以及低复杂度合二为一。
本文包括两个部分。在第一部分中,作为OTFS根基的数学原理会被解释清楚;在第二部分中,OTFS优于OFDM一类的多载波调制方法的性能增益将被演示,主要体现在以下应用场景:
- eMBB (Enhanced Mobile Broadband, 增强型移动宽带)。在本应用场景中,我们将演示在任意信道条件下,以最优化兼顾性能与复杂度为前提,OTFS是如何在MIMO的秩提高时使能频谱利用率的调整的
- IoT(Internet of Things物联网)。在本应用场景中,我们描述了一个在功率和延迟一定的情况下,可以最大化链路预算(以焦耳/比特为单位)并最小化重新发送次数的应用于小包的特定OTFS传输模式。这样就能达到增长电池寿命与增广信号覆盖度的目的。发送时使用OTFS信号,能在获取完全的时间分集增益的同时,保证低峰值平均功率比(PAPR—Peak to Average Power Ratio)与最大持续时间,从而最大化链路预算并最小化重发送的次数。
- 通信终端处于高速运动状态的应用场景,如V2V(交通工具间通信)与HST(高速铁路通信)。在这一应用场景中,我们展示了OTFS是如何最大化信息吞吐量、可靠性与性能稳定性的。我们还进一步展示了OTFS是如何在避免信道间串扰(ICI)的毁灭性影响的同时,利用多普勒效应作为一种新的分级来提升通信质量的。
- URLLC(超可靠低延迟通信)。在这一应用场景中,我们展示了OTFS对窄带干扰的抵抗能力,这一能力使URLLC的包能在存在窄带干扰的情况下仍保持良好状态。
- 毫米波通信的潜在应用场景。对这一应用场景的讨论其实是的对进行中的高相位噪声情况下OTFS通信的潜在应用的研究总结。内容上,我们将讲述如何在不牺牲信道容量的前提下通过OTFS来缓和相位噪声的不良影响。
2. OTFS原理
2.1 OTFS简述
OTFS这种调制方式将QAM符号复用到使用延迟-多普勒域表示的信号。延迟-多普勒域是一种全新的信号表达方式。在数学领域,延迟-多普勒形式通常被称为海森堡群的格形式(?lattice representation?群论吗?)。这一结构后来被物理学家进一步探索并拥有了新的称呼:Zak形式。OTFS将时域与频域整合到一起,成为了一种具有深远影响的调制方法。传统的TDM将QAM符号复用到连续的时间段上,而FDM将复用到连续的频段上。更广义地说,OTFS在雷达与通信间建立了一道概念性的桥梁。在2.2和2.3中,我们将解释这些理论。
OTFS波形受无线信道影响发生的变化能直接体现出物理环境的状况,从而可以由之推导出传输环境中会反射无线信号的反射体的高解析度雷达图。(?The OTFS waveforms optimally couple with the wireless channel in a way that captures the physics of the channel, yielding a high-resolution delay-Doppler Radar image of the constituent reflectors.?)这使信道和QAM符号间需要一种简单而对称的配对。这种对称性体现在三个基本属性上:
-
不变性
-
可分性
-
正交性
不变性代表了,对所有QAM符号而言,配对(?coupling,耦合?)模式都是相同的(所有符号都通过相同信道,换句话说,配对与传输过程无关)。可分性(?或者说Hardening?)代表了,所有的分集途径都是相互隔开的,每个QAM符号都会通过所属信道的所有分集途径。最后,正交性与意味着这种配对(?耦合?)是被定位的(?localized,受位置影响的?),也就是说,在接收端QAM符号仍然是接近相互正交的。这种正交性质与基于PN序列的传统CDMA调制有很大差异——在传统CDMA中,每个编码都为整体会引入新的干扰。不变性是相对于TDM和FDM而言的。在TDM与FDM中,配对(?耦合?)模式在不同的相干时间区间或相干频率区间都是有显著差异的。在第2.6节中,理论的这方面将被解释。
通过在延迟-多普勒域和对应的时间-频率域做二维(辛(?symplectic?,偶对的))傅里叶变换,OTFS的变体可以构筑在任意的多载波调制方案上。这种傅里叶式的关联引入了一族在时间-频率网格上的二维基函数,而每个基函数都可以被看成在多个tones(?)和多个多载波符号上的码字。这种交互使OTFS在形式上近于整合了CDMA的时间-频率扩展技术。在第2.7节中,理论的这一方面将被解释。
2.2 延迟-多普勒的信号表示方式
为了从根本上理解OTFS,重拾以两种基础信号表示方式为核心的信号处理基础是必须的。其一,时域表示方式,信号是一个以时间为变量的函数(由诸多delta函数组成);其二,频域表达方式,信号是一个以频率为变量的函数(由诸多复指数函数组成)。这两种表示方式可以用傅里叶变换相互转化。
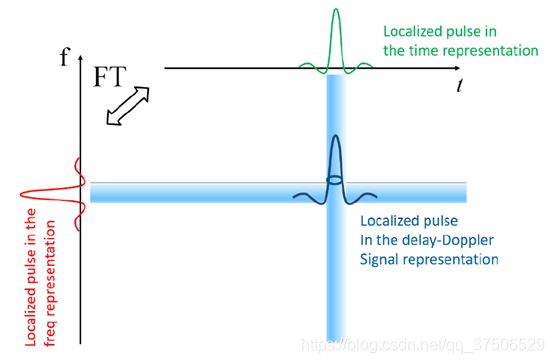
信号的时域表示方式和频域表示方式是互补的。若使用数学语言表达,这种互补性可由海森堡不确定性原理叙述:一个信号无法同时在任何时间或频率的维度被测定(?a signal cannot be simultaneously localized to any desired degree in time and in frequency.?)。具体地说,如果一个信号是时域上的,那它在频域上测不准(?non localized?);对应的,如果如果一个信号是频域上的,那它在时域上测不准,如图一所示。这一数学事实隐藏了更深层次的正向。结果表明,事实上是存在一种外显为可以同时被定位在任意时间或频率维度上的信号的,它具有一种同时适合延迟-多普勒雷达多目标探测与无线通信的属性。这种特殊的信号自然与定位在延迟-多普勒域上的脉冲有关。在延迟-多普勒域中的信号是在延迟-多普勒平面上的函数,而函数中的点是由(τ,ν)这两个变量作为参数的,τ为延迟,ν为多普勒(?频偏?)。
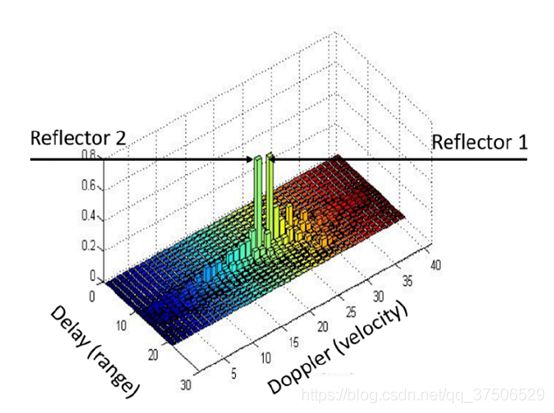
延迟-多普勒变量常用于雷达与通信理论中。在雷达领域中,延迟多普勒变量被用于表示和分辨移动中的物体——它们具有不同的延迟(距离)和多普勒(速度)特征。在通信中,它们被用于表示信道的时移与频移的特征。延迟-多普勒的信道表示方法在无线通信中具有尤为重大的意义,特别是在与包含了环境中的反射物的延迟-多普勒雷达图共同作用的场景中【4】。图2,展示了一条含有两个延迟(距离)相近但速度(多普勒)特性不同的反射物的信道的延迟-多普勒图像。
用延迟-多普勒表示信道已经广为人知,但廖为人知的是,这些变量也可以用于表示承载了信息的信号——以一种与延迟-多普勒形式的信道相和谐的方式。延迟-多普勒式的信号的数学表示非常微妙,并且需要引入一类新的函数——准周期函数。为了不这样(?to end this?),我们选择了一个延迟周期τ_r和多普勒周期ν_r,并使二者满足τ_r⋅ν_r=1,从而定义了一块单位面积的方形区域,如图3所示。一个延迟-多普勒信号是一个满足如下准周期条件的函数
ϕ(τ+nτ_r,ν+mν_r )=e^j2π(nντ_r-mτ_r ) ϕ(τ,ν)
这意味着此函数的周期性是由相位的倍数决定的,换句话说,函数值在每增加一个延迟周期τ_r时会获得一个等于e^(j2πντ_r )的相位系数,对应的,在每增加一个多普勒周期ν_r时会获得一个等于e^(-j2πτν_r )的相位系数。
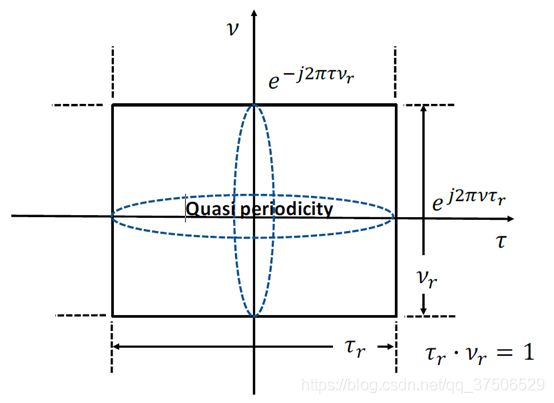
图3.延迟-多普勒准周期性
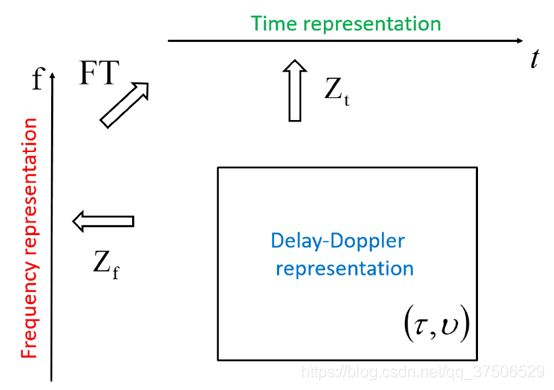
总之,信号的基本表示方法有三种。其一,与时间相关的函数;其二,与频率相关的函数;其三,与延迟-多普勒相关的准周期函数。这三种可以相互顶替的表示方法可以通过正则变换相互转化,如图4所示。时域与频域间的相互转化可有傅里叶变换完成;延迟-多普勒域与时域或频域间的转化分别由Zak变换完成,(Z_t 和Z_f)(【5】【6】【7】【8】)。Zak变换由周期性积分方程组成:
Z_t (ϕ)=∫_0(ν_r)▒〖ej2πtν ϕ(t,ν)dν〗
Z_f (ϕ)=∫_0(τ_r)▒〖e(-j2πtν) ϕ(τ,f)dτ〗
也就是说,到时域的Zak变换是由经过一个多普勒周期的逆傅里叶变换推出的,对应的,到频域的多普勒变换是由经过一个延迟周期的傅里叶变换推出的。我们注意到,对于Zak变换而言,准周期性是这种一对一的在一维轴和二维平面上的相等关系的前提。如果缺少准周期性,在一维轴上的信号会有无穷多个延迟-多普勒表示方法。
图4. 延迟-多普勒表示方法
2.3 信号处理的整体框架
待续… …
引用
[1] “NGMN 5G Initiative White Paper,” February 2015. [Online]. Available:
https://www.ngmn.org/uploads/media/NGMN_5G_White_Paper_V1_0.pdf.
[2] K. T. Truong and R. Heath, “Effects of channel aging in massive MIMO systems,”
Journal of Communications and Networks, vol. 15, no. 4, pp. 338-351, Aug 2013.
[3] E. Björnson, et al., “Massive MIMO Systems With Non-Ideal Hardware: Energy
Efficiency, Estimation, and Capacity Limits,” IEEE Transactions on Information
Theory, vol. 60, no. 11, pp. 7112-7139, Nov 2014.
[4] P. Bello, “Characterization of randomly time-variant linear channels,” IEEE
Transactions on Communications, vol. 11, no. 4, pp. 360-393, Nov 1963.
[5] J. Zak, in Phys. Rev. Lett 19, 1967.
[6] A. Janssen, “The Zak Transform: A signal transform for sampled time-continuous
signals,” Philips Journal of Research, January 1988.
[7] R. M. Lerner, “Representation of Signals,” in Lectures on Communication System
Theory, E. Baghdady, Ed., New York, McGraw-Hill, 1961, p. 241.
[8] E. Jury, in Theory and Application of the z-Transform Method, New York, John
Wiley, 1964, pp. 15-20.
[9] G. Caire and S. Shamai, “On the achievable throughput of a multi-antenna Gaussian
broadcast channel,” IEEE Transactions on Information Theory, vol. 43, pp. 1691-
1706, Jul 2003.
[10] T. Haustein, et al., “Performance of MIMO systems with channel inversion,” in
Proc. 55th IEEE Veh. Technol. Conf., Birmingham, AL, 2002.
[11] M. Tomlinson, “New automatic equaliser employing modulo arithmetic,” Electron.
Lett., vol. 7, pp. 138-139, Mar 1971.
[12] H. Harashima and H. Miyakawa, “Matched-transmission technique for channels
with intersymbol interference,” IEEE Transactions on Communications, Vols.
COM-20, pp. 774-780, Aug 1972.
[13] B. Hochwald, C. Peel and A. L. Swindlehurst, “A Vector-Perturbation Technique
for Near-Capacity Multiantenna Multiuser Communication — Part II:
Perturbation,” IEEE Transactions on Commiunications, vol. 53, no. 3, March 2005.
[14] Y. Carmon, S. Shamai and T. Weissman, “Comparison of the Achievable Rates in
OFDM and Single Carrier Modulation with I.I.D. Inputs,” IEEE Transactions on
Information Theory, vol. 61, no. 4, pp. 1795-1818, Apr 2015.
[15] C. Peel, B. Hochwald and A. Swindlehurst, “A Vector-Perturbation Technique for
Near-Capacity Multiantenna Multiuser Communication — Part I: Channel
Inversion and Regularization,” IEEE Transactions on Communications, vol. 53, no.
1, Jan 2005.