Verilog学习 | 数字下变频与脉冲压缩的综合仿真与硬件实现
目录
一、 任务介绍
二、基本原理
2.1 数字下变频（Direct Digital Controller,DDC）
2.2 脉冲压缩（Pulse Compression,PC）
三、基于MATLAB的仿真实现
3.1 回波信号的产生
3.2 数字下变频
3.3 脉冲压缩
3.4 仿真结果
四、基于Vivado的仿真实现
4.1 回波数据产生
4.2 数字下变频部分
4.2.1 混频
4.2.2 低通滤波
4.2.3 抽取
4.3 脉冲压缩
4.3.1 利用MATLAB生成滤波器系数
4.3.2 FIR滤波器配置
4.3.3 滤波器例化
4.3.4 求模
4.4 仿真结果
五、基于Vivado的硬件实现
六、结语
参考文献
一、 任务介绍
实际雷达系统工作重频1ms，接收机中频为30MHz，发射信号带宽为2MHz，时宽为50us的线性调频信号，假定接收机噪声（高斯白噪声）AD采样（采样率为40MHz）后的量化位数为6位，距离雷达100Km有一理想点目标，该点目标回波强度的信噪比为60DB，利用MATLAB产生雷达单次发射的中频回波接收数据，量化为16位有符号整数，存到FPGA中的RAM中，然后在FPGA中对该中频回波数据进行数字下变频处理（包括移频、滤波和抽取3步操作），得到基带的I/Q数据（采样数据率降为4MHz），并对该线性调频信号进行脉冲压缩处理（加汉明窗进行副瓣压制）。同时结合实际处理过程考虑FPGA中的每一级处理的截位该如何处理（既要保证噪声幅度不变，又要保证结果不能溢出）以及如何从回波数据中确定目标的真实距离值。
二、基本原理
该系统旨在脉冲压缩系统的实现，该系统包括三部分：MATLAB生成回波数据部分、数字下变频（DDC）部分以及脉冲压缩（PC）部分，以下对后两部分原理进行简单的介绍。
2.1 数字下变频（Direct Digital Controller,DDC）
为了便于数据处理以及缓解系统的数据压力，常常需要采用数字下变频(DDC)技术,将采样得到的高速率信号变成低速率基带信号。DDC的主要结构包括三部分，分别是变频，低通滤波，采样速率转换（数据抽取）。由于正交直接下变频技术采用正交的I/Q路本振信号进行混频，有效抑制镜频现象，并且给后续的数据处理带来了极大的便利，因此大部分数字下变频器采用了该技术，下图即正交直接下变频技术的结构框图。
首先，中频信号
经A/D采样后成数字中频信号
,其表达式如下：
经I与Q路正交混频后,
![f_{I}(n)cos(2\pi f_{0}nT) cos(2\pi f_{0}nT)={\frac{1}{2}}[ f_{I}(n) - f_{I}(n)cos(4\pi f_{0}nT)]](http://img.e-com-net.com/image/info8/5967d0c8be5f4940903ef9c785b7970d.gif){kind=small}
![f_{Q}(n)sin(2\pi f_{0}nT) sin(2\pi f_{0}nT)={\frac{1}{2}}[ f_{Q}(n) - f_{Q}(n)cos(4\pi f_{0}nT)]](http://img.e-com-net.com/image/info8/3f77c117e2b842b3ae22b1a3cc1bca4c.gif){kind=small}
经低通滤波（LPF）后，可得到两路正交基带信号
与
，也即荷载着有用信息的信号的实部与虚部，方便了后续的复数运算及相关的数据处理。而有时LPF的输入端的数据率很大，一般的FIR滤波器可能无法达到这个处理速率，因此可以先通过级联积分梳状（CIC）和半带（HB）滤波器进行滤波并对数据进行大的抽取，降低数据率便于FIR进行滤波。本实验中的数据率不大，因此采用直接FIR进行滤波。
降为基带的信号此时已经不需要太高的采样率，为了降低数据率，需要在最后进行数据抽取的处理。
2.2 脉冲压缩（Pulse Compression,PC）
脉冲压缩技术是雷达在发射机峰值功率受限情况下，为提高目标探测距离，同时保持较高的距离分辨力而采用的一 种有效技术（也即大时宽脉宽积）。其原理是将回波信号与原信号做相关运算从而得出相关峰，本质上是将不同频率信号的能量累加起来得到一个较好的信噪比。
脉冲压缩有两种实现方法，一类是在频域上进行处理，将零中频回波信号进行快速傅里叶变换，然后与发射信号的频谱相乘，然后再进行逆傅里叶变换得出结果；另一类是时域处理法，将零中频信号与回波信号进行卷积得出结果。本工程中采用的是时域处理方法。
设雷达系统采用的波形为线性调频波（LFM），则基带信号为：
其中，a(t)为信号包络，也即门宽为
的矩形脉冲，k为调频斜率，经过调制（上变频）后形成发射信号：
其中 ，
为信号中频。接收信号为：
N(t)为接收机输入噪声，可用白噪声进行代替。经过DDC后脉压系统的输入信号为
根据柯西-施瓦茨不等式可推知（具体推导过程可参文末参考文献[1]），当滤波器的输出信号达到最大信噪比时，匹配滤波器系数是输入基带信号的共轭翻转：
其中，
是滤波器的物理延迟，在理论分析时可将其视为0。由上式可知，匹配滤波器的作用时对输入信号
做相关处理，由于滤波器系数与信号中
具有强相关特性，而与噪声
相关性较弱，因此可利用此特性进行脉冲宽度压缩以及距离测量。有用基带信号经脉压后为：
![S_{o}(t) = H(t)*S_{b}(t-t_{d})=\sqrt{k\tau^{2}}{\frac{sin[2\pi k(t-t_{d})\tau/2]}{2\pi k(t-t_{d})\tau/2}}e^{j2\pi[-{\frac{k}{2}}(t-t_{d})^{2}]}e^{j{\frac{\pi}{4}}}](http://img.e-com-net.com/image/info8/718b8c1743bc4cf5bb5d492c87c322ab.gif){kind=small}
由上式可知，基带信号经脉压后是Sa函数的形式， 当
时输出信号具有最大值，此时可通过下式计算目标距离：
此外，由Sa函数的特性可知，输出信号的-4dB主瓣宽度为1/B,则脉冲压缩比为
,对于一般的时宽为的脉冲信号，其带宽约为
，因此其时宽带宽积约为1。当采用的波形为线性调频信号时，B的取值可独立于，因此可获得压缩比大于1的输出信号，因此可提高分辨率的同时提高探测距离。
三、基于MATLAB的仿真实现
为了探究算法系统的性能，首先在MATLAB平台上进行仿真实现，将该脉压系统分为回波信号产生部分、数字下变频部分以及脉冲压缩部分三个部分进行编程。
3.1 回波信号的产生
首先根据雷达探测最小距离和最大距离确定接收窗，并根据任务要求的参数产生回波信号，代码如下：
%% 参数初始化
% clc,clear;
C=3e8; %光速
T=50e-6; %脉冲宽度50us
Tr=1e-3; %脉冲重复周期
Fc=30e6; %LFM载频
B=2e6; %频带宽度2MHz
K=B/T; %调频斜率
Fs=40e6;Ts=1/Fs; %采样频率与采样时间
%% 雷达接收窗
Rmin=10e3;Rmax=150e3; %测距范围
R=[100e3]; %目标点的位置，每一个目标相对于雷达的斜距
M=length(R); %目标的个数
RCS=[1]; %雷达截面积，一维数组
Rwid=Rmax-Rmin; %最大测距长度
Twid=2*Rwid/C; %回波窗的长度
Nwid=ceil(Twid/Ts); %采样窗内的采样点数
t=linspace(2*Rmin/C,2*Rmax/C,Nwid); %回波窗
%% 产生回波
td=ones(M,1)*t-2*R'/C*ones(1,Nwid); %回波时间序列
Srt=real(RCS*(exp(2j*pi*(Fc*td+1/2*K*td.^2)).*(abs(td)3.2 数字下变频
注意在DDC的输入端是一个A\D采样器，根据Nyquist采样定理知，若使采样后信号频谱不混叠，采样速率须大于二倍的信号最高频率分量
。但由于采样频率过大一方面需采用性能更佳的采样器，另一方面过大的数据量会对整个系统的数据处理能力造成压力，为了解决这一问题，需采用带通信号采样。
事实上，带通信号采样要求的特点是：采样率高于只是保证采样后不发生频谱混叠的必要条件，而非充分条件。若要使得采样后的频谱不发生混叠，同样可以用小于的采样率进行采样。而为了在保证不发生频谱混叠的情况下便于滤除负频带，对带通信号采样时可采取最佳采样频率：
式中，表示信号中频，m是满足
的正整数。
注意到在采用最佳采样频率的情况下，DDC两路混频信号分别为：
![cos[2\pi f_0n/f_{s}]=cos(nm\pi-n\pi/2)=\left\{\begin{matrix}(-1)^{n/2},n\ is\ even & \\ 0\ \ \ \ \ \ \ ,n\ is\ odd & \end{matrix}\right.](http://img.e-com-net.com/image/info8/e56904bd9f8248e5ac8aab11ef14b75d.gif){kind=small}
![sin[2\pi f_0n/f_{s}]=sin(nm\pi-n\pi/2)=\left\{\begin{matrix}0\ \ \ \ \ \ ,n\ is\ even & \\ (-1)^{m}(-1)^{(n-1)/2},n\ is\ odd & \end{matrix}\right.](http://img.e-com-net.com/image/info8/8cb7de081e304e7683902b1e0f84fe8d.gif){kind=small}
由于任务要求中为30MHz，
为40MHz，因此满足最佳采样频率，且m为2，此时I路本振信号为[1,0,-1,0]的周期循环，Q路本振信号为[0,1,0,-1]的周期循环。
混频之后利用MATLAB的fdatool工具箱设计低通滤波器，得到滤波器系数，滤除掉高频信号，此处给出设计图如下：
导出滤波器系数到Num数组中。进行滤波后分别对两路信号进行10倍的抽取从而将40MHz降为4MHz。DDC完整代码如下：
%% 数字下变频
%频移
n = 1:length(Srt);
cos_unit = [1,0,-1,0];
cos_osc =cos_unit(mod(n,4)+1);
sin_unit = [0,1,0,-1];
sin_osc =sin_unit(mod(n,4)+1);
DDC_out_i1 = Srt.*cos_osc;
DDC_out_q1 = Srt.*sin_osc;
figure(1);
subplot(211);
plot(t*1e6,DDC_out_i1);
axis([600 700 -2 2]);
subplot(212);
plot(t*1e6,DDC_out_q1);
axis([600 700 -2 2]);
%滤波
DDC_out_i = conv(Num,DDC_out_i1);
DDC_out_q = conv(Num,DDC_out_q1);
figure(2);
subplot(211);
plot(DDC_out_i);
axis([22e3 26e3 -1 1]);
subplot(212);
plot(DDC_out_q);
axis([22e3 26e3 -1 1]);
%抽取
deciN = 10;
DDC_out_i_deci = DDC_out_i(1:deciN:length(DDC_out_i));
DDC_out_q_deci = DDC_out_q(1:deciN:length(DDC_out_q));
figure(3);
subplot(211);
plot(DDC_out_i_deci);
axis([22e2 26e2 -1 1]);
subplot(212);
plot(DDC_out_q_deci);
axis([22e2 26e2 -1 1]);3.3 脉冲压缩
得到DDC后的两路正交信号后，即得到基带信号的实部信号
和虚部信号
，再将滤波器分为实部与虚部滤波器，其系数分别为H(t)的实部
与虚部
,则滤波过程为：
这样可将复数的运算转化为4个实数的滤波过程，之后对上式中的实数与虚数部分进行求模即可，给出脉压部分代码如下：
%% 脉冲压缩
t_base = -T/2:1/Fs:T/2; %时间序列
h = exp(-1j*K*pi*t_base.^2);%信号基带复共轭
hi = real(h);%匹配系数实部
hq = imag(h);%匹配系数虚部
hiw = floor(hi' .*hamming(length(hi)));%系数实部加窗后量化
hqw = floor(hq' .*hamming(length(hq)));%系数虚部加窗后量化
hiw_deci = hiw(1:deciN:length(hiw));
hqw_deci = hqw(1:deciN:length(hqw));
PC_hisi = conv(hiw_deci,DDC_out_i_deci);
PC_hisq = conv(hiw_deci,DDC_out_q_deci);
PC_hqsi = conv(hqw_deci,DDC_out_i_deci);
PC_hqsq = conv(hqw_deci,DDC_out_q_deci);
PC_i = PC_hisi - PC_hqsq;
PC_q = PC_hisq + PC_hqsi;
PC_final = sqrt(PC_i.^2 + PC_q.^2) ;
% PC_result = PC_i + 1j*PC_q;
% PC_final = db(abs(PC_result));
dis=linspace(Rmin,Rmax,length(PC_final)); %回波窗
figure(4);
plot(dis,PC_final);
axis([Rmin Rmax 0 100]);3.4 仿真结果
运行程序后，可得到回波信号如下：
由于任务要求的信噪比较大，回波图形中几乎看不到噪声的影响。
DDC混频后信号图像如下：
低通滤波后信号图像如下：
抽取后信号图像如下：
脉压结果图像如下：
可见脉压误差在1Km左右，系统仿真结果良好。
四、基于Vivado的仿真实现
基于Vivado的仿真思路与MATLAB仿真相似，除部分滤波器需要额外配置外，只需将MATLAB语言翻译为Verilog即可，先给出笔者手画的系统框图如下：
因此可根据上图列出顶层文件的输入输出管脚如下：
//脉冲压缩顶层文件
module PC_top(
input wire clk_100M, //系统时钟100MHz
input wire rst_n, //复位按钮
output wire signed [34:0] DDC_out_i,//数字下变频后的I路信号
output wire signed [34:0] DDC_out_q,//数字下变频后的Q路信号
output wire signed [47:0] PC_final //脉冲压缩处理后信号
);以下对各部分的编程实现做以介绍。
4.1 回波数据产生
根据任务中的参数要求以及信号与噪声的量化位数，可得到回波数据的.txt文件，具体过程详见程序注释，此处就不赘述了：
%% 参数初始化
clc,clear;
C=3e8; %光速
T=50e-6; %脉冲宽度50us
Tr=1e-3; %脉冲重复周期
Fc=30e6; %LFM载频
B=2e6; %频带宽度2MHz
K=B/T; %调频斜率
Fs=40e6;Ts=1/Fs; %采样频率与采样时间
%% 雷达接收窗
Rmin=10e3;Rmax=150e3; %测距范围
R=[100e3]; %目标点的位置，每一个目标相对于雷达的斜距
M=length(R); %目标的个数
RCS=[1]; %雷达截面积，一维数组
Rwid=Rmax-Rmin; %最大测距长度
Twid=2*Rwid/C; %回波窗的长度
Nwid=ceil(Twid/Ts); %采样窗内的采样点数
t=linspace(2*Rmin/C,2*Rmax/C,Nwid); %回波窗
%% 产生回波
td=ones(M,1)*t-2*R'/C*ones(1,Nwid); %回波时间序列
Srt=RCS*(exp(2j*pi*(Fc*td+1/2*K*td.^2)).*(abs(td)注意，产生回波数据后，需要将文末的“,”换为“;”
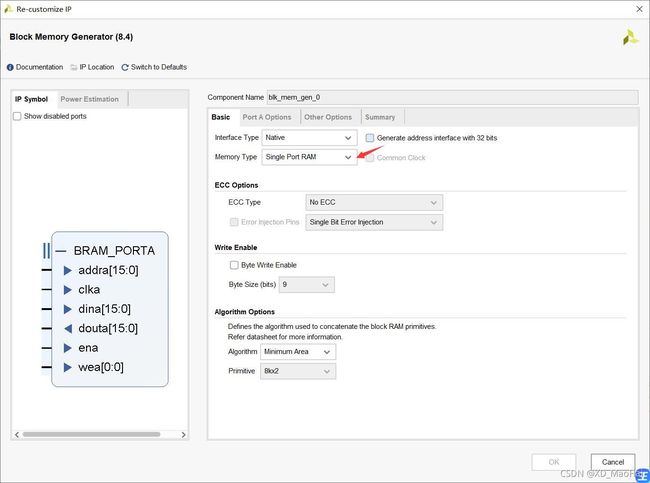
此时已经得到回波数据.txt文件，但是导入RAM里需要将之格式换为.coe，此部可通过直接更改文件拓展名完成。 此步完成后，根据采样点数配置RAM的IP核：
之后导入生成的.coe文件进行初始化：
配置完成后，需要按时钟读出回波数据，而RAM的读数实则就是对地址的控制，此处选择对回波循环读数：
//RAM例化
wire [15:0] dina; //输入信号（本工程已利用MATLAB初始化了RAM）
reg [15:0] addr = 0; //地址初始化
wire signed [15:0] dout;//读出回波数据
blk_mem_gen_0 echo_ad (
.clka(clk_100M), // input wire clka
.ena(1'b1) , // input wire ena
.wea(1'b0) , // input wire [0 : 0] wea
.addra(addr) , // input wire [15 : 0] addra
.dina(dina) , // input wire [15 : 0] dina
.douta(dout) // output wire [15 : 0] douta
);
//按时钟读出回波信号数据
always @ (posedge clk_100M) begin
if(addr == 16'd37334) begin //注意此处地址上限值是数据深度
addr <= 16'd0;
end
else begin
addr <= addr + 1'b1;
end
end4.2 数字下变频部分
4.2.1 混频
同MATLAB仿真相似，由于本工程中采样率满足最优采样频率，只需将I,Q两路信号分别乘以周期循环的固定数组即可：
/*混频：由于本项目中采用的是最优采样频率（4f_0/(2m+1)），又根据取的m值为1，
因此I、Q路的本振信号分别是[1,0,-1,0]、[0,1,0,-1]的周期序列，
若不满足最优采样频率可添加DDS进行混频*/
reg [1:0] count = 0; //计数器用以计数状态
reg signed [15:0] DDC_out_i1=0; //混频后的I路信号
reg signed [15:0] DDC_out_q1=0; //混频后的Q路信号
wire signed [15:0] AD_in_p; //回波原信号
wire signed [15:0] AD_in_n; //回波原信号相反数
assign AD_in_p = dout;
assign AD_in_n = ~dout[15:0] + 16'd1;//！硬件语言中的取相反数操作
always @ (posedge clk_100M) begin
count <= count + 1;
case(count)
2'd0:begin
DDC_out_i1 <= AD_in_p;
DDC_out_q1 <= 0;
end
2'd1:begin
DDC_out_i1 <= 0;
DDC_out_q1 <= AD_in_p;
end
2'd2:begin
DDC_out_i1 <= AD_in_n;
DDC_out_q1 <= 0;
end
2'd3:begin
DDC_out_i1 <= 0;
DDC_out_q1 <= AD_in_n;
end
endcase
end需要注意，硬件语言中的取反操作并非简单的改变符号位，因为机器中以补码形式存储数据，因此取反操作应为：
AD_in_n = ~dout[15:0] + 16'd1;当然，若采样频率不满足最优采样率，利用DDS生成等于信号中频频率的正余弦波与信号点乘即可完成混频。
4.2.2 低通滤波
将MATLAB仿真部分生成的滤波器系数导出成.coe文件，再导入到FIR的IP核中进行配置，对FIR配置不太清晰的朋友可参笔者之前文章：
Verilog学习 | 基于vivado平台的DDS、FIR、FFT核的综合学习使用
https://blog.csdn.net/qq_56937808/article/details/119799996?spm=1001.2014.3001.5501
此处直接给出配置过程如下：
为了简化程序，提高程序可读性，可额外构造一个fir_lpf文件：
//DDC低通滤波处理
module fir_lpf(
input wire clk_100M,//系统时钟100MHz
input wire rst_n ,//复位按钮（低电平有效）
input wire signed [15:0] dina ,//回波数据信号输入
output wire signed [34:0] dout //滤波输出
);
//滤波器初始化
reg s_axis_data_tvalid;
wire s_axis_data_tready;
wire m_axis_data_tvalid;
wire signed [39:0] m_axis_data_tdata;
assign dout = m_axis_data_tdata[34:0];//截取输出信号的低35位
//复位时拉高数据有效电平
always @ (posedge clk_100M or negedge rst_n) begin
if(!rst_n) begin
s_axis_data_tvalid <= 1'b1;
end
end
//FIR的IP核例化
fir_compiler_0 inst_lpf (
.aresetn(rst_n), // input wire aresetn
.aclk(clk_100M), // input wire aclk
.s_axis_data_tvalid(1'b1), // input wire s_axis_data_tvalid
.s_axis_data_tready(s_axis_data_tready), // output wire s_axis_data_tready
.s_axis_data_tdata(dina), // input wire [15 : 0] s_axis_data_tdata
.m_axis_data_tvalid(m_axis_data_tvalid), // output wire m_axis_data_tvalid
.m_axis_data_tdata(m_axis_data_tdata) // output wire [39 : 0] m_axis_data_tdata
);
endmodule最后在顶层文件中进行两次例化生成I，Q两路滤波器即可：
/*低通滤波：滤除混频后的高频部分与带外白噪声。
滤波器系数由MATLAB的fda工具箱产生*/
fir_lpf lpf_i(
.clk_100M(clk_100M),
.rst_n(rst_n),
.dina(DDC_out_i1),
.dout(DDC_out_i)
);//I路低通滤波
fir_lpf lpf_q(
.clk_100M(clk_100M),
.rst_n(rst_n),
.dina(DDC_out_q1),
.dout(DDC_out_q)
);//Q路低通滤波4.2.3 抽取
硬件语言的抽取不同于MATLAB的抽取，MATLAB只需对数组进行跨步读取数组就好，但是硬件语言中，各器件是按时钟运行的，无法在得到整个数据的情况下进行跨步读取。事实上，硬件语言的抽取也很简单，只需设置一个计数器，每隔10个时钟将后续滤波器的s_axis_data_tvalid拉高，其余时间保持低电平即可。
//10分频
always @ (posedge clk_100M) begin
if(cnt_deci == 4'd10) begin
cnt_deci <= 0;
s_axis_data_tvalid <= 1;
end
else begin
cnt_deci <= cnt_deci + 1;
s_axis_data_tvalid <= 0;
end
end4.3 脉冲压缩
对原理进行了上述的介绍后，可知脉冲压缩其实就是滤波的过程，而基于Vivado的脉压过程就是对FIR滤波器的配置。
4.3.1 利用MATLAB生成滤波器系数
由第二部分对脉压原理的介绍，可知两路FIR滤波器系数即是LFM基带信号共轭翻转的实部和虚部，由此可利用MATLAB生成两路滤波器系数：
%% 参数初始化
clc,clear;
C=3e8; %光速
T=50e-6; %脉冲宽度50us
Tr=1e-6; %脉冲重复周期
Fc=30e6; %LFM载频
B=2e6; %频带宽度2MHz
K=B/T; %调频斜率
Fs=4e6;Ts=1/Fs; %采样频率与采样时间
%% 生成本地匹配滤波器
deciN = 10;
width = 16;%数据宽度（量化位数）
t = -T/2:1/Fs:T/2; %时间序列
h = exp(-1j*K*pi*t.^2);%信号基带复共轭
hi = real(h);%匹配系数实部
hq = imag(h);%匹配系数虚部
hiw = floor(hi' * (2^(width-1)-1).*hamming(length(hi)));%系数实部加窗后量化
hqw = floor(hq' * (2^(width-1)-1).*hamming(length(hq)));%系数虚部加窗后量化
hiw_deci = hiw(1:deciN:length(hiw));
hqw_deci = hiw(1:deciN:length(hqw));
%% 生成匹配系数实部.coe文件
fid_i = fopen('F:\Verilog_trails\ex_PulseCompression\ex_PulseCompression\GeneratePc_I.txt','w');%生成.txt文件
fprintf(fid_i,'Radix = 10; \n');
fprintf(fid_i,'Coefficient_Width = 16; \n');
fprintf(fid_i,'CoefData = \n');
fprintf(fid_i,'%d,\n',hiw_deci);%将采样数据输入文件中
fclose all;%关闭文件
%% 生成匹配系数虚部.coe文件
fid_q = fopen('F:\Verilog_trails\ex_PulseCompression\ex_PulseCompression\GeneratePc_Q.txt','w');%生成.txt文件
fprintf(fid_q,'Radix = 10; \n');
fprintf(fid_q,'Coefficient_Width = 16; \n');
fprintf(fid_q,'CoefData = \n');
fprintf(fid_q,'%d,\n',hqw_deci);%将采样数据输入文件中
fclose all;%关闭文件
4.3.2 FIR滤波器配置
同上述DDC的低通滤波器配置过程，生成两路滤波器系数的.coe文件，并将之导入到FIR的IP核中：
其余FIR配置如下：
4.3.3 滤波器例化
同DDC的低通滤波器例化，额外创建PulseCompress_hi与PulseCompress_hq文件：
//脉压滤波器_I路（系数为LFM信号的实数部分）
module PulseCompress_hi(
input clk_100M, //系统时钟100MHz
input s_axis_data_tvalid,//数据有效电平
input wire signed [34:0] din, //数据输入
output wire signed [53:0] dout //数据输出
);
//FIR引脚初始化
wire s_axis_data_tready;
wire m_axis_data_tvalid;
wire signed [55:0] m_axis_data_tdata ;
//FIR例化
Compress_hi inst_hi(
.aclk(clk_100M), // input wire aclk
.s_axis_data_tvalid(s_axis_data_tvalid), // input wire s_axis_data_tvalid
.s_axis_data_tready(s_axis_data_tready), // output wire s_axis_data_tready
.s_axis_data_tdata({{5{din[34]}},din}), // input wire [39 : 0] s_axis_data_tdata
.m_axis_data_tvalid(m_axis_data_tvalid), // output wire m_axis_data_tvalid
.m_axis_data_tdata(m_axis_data_tdata) // output wire [55 : 0] m_axis_data_tdata
);
assign dout = m_axis_data_tdata[53:0];//截取FIR输出的低54位
endmodule//脉压滤波器_Q路（系数为LFM信号的虚数部分）
module PulseCompress_hq(
input clk_100M, //系统时钟100MHz
input s_axis_data_tvalid,//数据有效电平
input wire signed [34:0] din, //数据输入
output wire signed [53:0] dout //数据输出
);
//FIR引脚初始化
wire s_axis_data_tready;
wire m_axis_data_tvalid;
wire signed [55:0] m_axis_data_tdata ;
//FIR例化
Compress_hq inst_hq(
.aclk(clk_100M), // input wire aclk
.s_axis_data_tvalid(s_axis_data_tvalid), // input wire s_axis_data_tvalid
.s_axis_data_tready(s_axis_data_tready), // output wire s_axis_data_tready
.s_axis_data_tdata({{5{din[34]}},din}), // input wire [39 : 0] s_axis_data_tdata
.m_axis_data_tvalid(m_axis_data_tvalid), // output wire m_axis_data_tvalid
.m_axis_data_tdata(m_axis_data_tdata) // output wire [55 : 0] m_axis_data_tdata
);
assign dout = m_axis_data_tdata[53:0];//截取FIR输出的低54位
endmodule
最后在顶层文件中对其例化即可：
//对DDC的I路信号进行I路的脉冲压缩
PulseCompress_hi hisi(
.clk_100M(clk_100M),
.s_axis_data_tvalid(s_axis_data_tvalid),
.din(DDC_out_i),
.dout(PC_hisi)
);
//对DDC的Q路信号进行I路的脉冲压缩
PulseCompress_hi hisq(
.clk_100M(clk_100M),
.s_axis_data_tvalid(s_axis_data_tvalid),
.din(DDC_out_q),
.dout(PC_hisq)
);
//对DDC的I路信号进行Q路的脉冲压缩
PulseCompress_hq hqsi(
.clk_100M(clk_100M),
.s_axis_data_tvalid(s_axis_data_tvalid),
.din(DDC_out_i),
.dout(PC_hqsi)
);
//对DDC的Q路信号进行Q路的脉冲压缩
PulseCompress_hq hqsq(
.clk_100M(clk_100M),
.s_axis_data_tvalid(s_axis_data_tvalid),
.din(DDC_out_q),
.dout(PC_hqsq)
);4.3.4 求模
进行4次卷积，也即FIR滤波后，可得到滤波后信号的实部和虚部：
//两路脉冲压缩后的信号
wire signed [54:0] PC_i;//实部信号
wire signed [54:0] PC_q;//虚部信号
//按照复数的乘法规则进行各路信号的相加减运算得到脉压后的实部和虚部信号
assign PC_i = {PC_hisi[53],PC_hisi}- {PC_hqsq[53],PC_hqsq};//实部信号
assign PC_q = {PC_hisq[53],PC_hisq}+ {PC_hqsi[53],PC_hqsi};//虚部信号最后对信号进行求模即可得到脉压结果：
assign PC_final = $signed(PC_i[54:31])* $signed(PC_i[54:31])+ $signed(PC_q[54:31])* $signed(PC_q[54:31]);此处为了减少脉压结果的数据位宽，对实部和虚部信号进行了高位截取。
4.4 仿真结果
创建Testbench文件进行仿真，给出复位和时钟信号：
//Testbench
module tb_echo;
reg clk_100M ;//系统时钟为100MHz
reg rst_n ;//复位按钮（低电平有效）
wire signed [34:0] DDC_out_i ;//数字下变频后的I路信号
wire signed [34:0] DDC_out_q ;//数字下变频后的Q路信号
wire signed [47:0] PC_final ;//脉冲压缩处理后信号
//初始化
initial begin
clk_100M = 0;
rst_n = 0;
#100
rst_n = 1;
end
//系统时钟产生
always #5 clk_100M <= ~clk_100M;
//顶层文件例化
PC_top inst_echo(
.clk_100M(clk_100M),
.rst_n(rst_n),
.DDC_out_i(DDC_out_i),
.DDC_out_q(DDC_out_q),
.PC_final(PC_final)
);
endmodule运行程序后，得到各阶段波形图如下：
可见脉压信号PC_final的峰值出现时间约为243us，又因为系统时钟为100MHz，采样率为40MHz，即40MHz的数据以100MHz速度读出，所以目标实际距离为：
可见误差在1km左右，仿真效果良好。
五、基于Vivado的硬件实现
本工程中选择是Zynq-7000系列的一块板子，由于硬件调试工作都是在实验室完成的，好多过程截图都没有保存，因此笔者仅能根据记忆将调试过程以文字的方式罗列如下：
Step1：给需要观测的信号设置MARK_DEBUG，本工程中我们仅需要观测最后的脉压信号PC_final，因此对其进行设置：
(*MARK_DEBUG = "TRUE"*) wire signed [47:0] PC_final;Step2：设置ILA核抓取信号：
ila_0 ILA ( .clk(clk_100M), // input wire clk .probe0(PC_final) // input wire [47:0] probe0 );Step3：配置Clocking Wizard，利用板子的晶振生成需要的系统时钟：
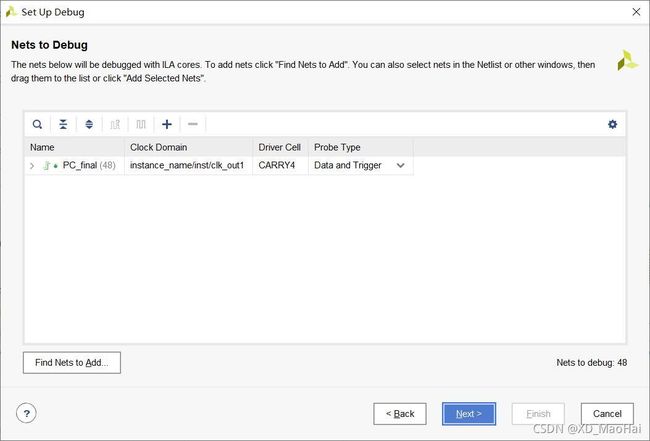
clk_wiz_0 instance_name ( // Clock out ports .clk_out1(clk_100M), // output clk_out1 // Status and control signals .reset(rst_n), // input reset .locked(locked), // output locked // Clock in ports .clk_in1(clk_in1)); //输入的板子晶振Step4：开始综合，综合成功后进行Set Up Debug，选择PC_final进行观测：
Step5：开始实现，实现完成后生成生成比特流。
Step6：最后给板子上电，将生成的比特流烧入板子中，通过ILA生成的波形窗进行观测。
这里给出调试现场如下：
最后ILA显示的波形窗如下：
注意到除100km（峰值较小）外，波形窗中还添加了50km（峰值较大）的参考目标。这是因为ILA输出信号的观察初始点是随机选取的，单纯只有目标的情况下，无法确定目标回波延时，因此需要设置参考目标进行相对观测。
根据波形窗，实际目标与参考目标之间相差40730-27430=13300个采样点，因此实际目标距离为：
可见误差不足150米，测距效果较好。
六、结语
该工程前后足足花费了我一个多月的时间，从基础原理学习到MATLAB、Vivado的仿真实现，再到后来的上板实操，该工程虽仅仅实现了简单的脉压系统，但对于一个初学者而言，其涵盖之广，机理之深，编程之繁，已让笔者一度穷经皓首了。但也正是这样具有挑战性的工程，才能淬炼一个人的科研素养与钻研精神，拓宽知识领域，也希望自己依旧能保持这种学习的激情和动力，在科研的路上不断开拓进取！
最后还是要十分感谢实验室中的龚学长、陆学长、魏学长和老师的悉心指导！！！
参考文献
[1] 姜文博. FPGA实现高速雷达信号脉冲压缩处理[D]. 西安电子科技大学, 2016.
[2] 阎炜. 数字下变频器核脉冲压缩的研究与设计[D]. 陕西:西安电子科技大学,2014. DOI:10.7666/d.D549115.
[3]线性调频（LFM信号）脉冲压缩雷达matlab仿真- 脉冲压缩 测距 测速 距离速度三维像（附matlab代码）_格桑蓝莲的博客-CSDN博客_lfm信号
[4] 史林,赵树杰. 数字信号处理[M]. 科学出版社, 2007.