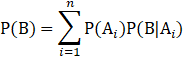【机器学习基础】朴素贝叶斯进行垃圾邮件分类

目录

    一 朴素贝叶斯简介

    二 贝叶斯决策理论

    三 朴素贝叶斯进行垃圾邮件分类

    3.1构造数据集

    3.2 构造词典

    3.3 构造词集模型

    3.4 求解先验概率和条件概率

    3.5 对样本集进行分类

    3.6 交叉验证

    四 整体代码实现

    五 参考材料

---

    一 朴素贝叶斯简介

    贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。朴素贝叶斯是贝叶斯决策理论的一部分，所以本文首先介绍贝叶斯决策理论，然后我们通过实例来介绍最简单的一种贝叶斯分类：朴素贝叶斯。

 

    二 贝叶斯决策理论

    首先是条件概率公式：

                                                

 

    如上图所示，P(A|B) 表示已知事件B发生的前提下，事件A发生的概率，用上图来说，就是AB交界那部分的面积与B的面积的比例，所以 ，同理 ，再整合全概率公式就可以得到贝叶斯公式了，全概率公式如下：

                                                

这里的事件组A需要满足一定的条件：

1. 两 两两互斥
2. ，则称事件组A是空间Ω的一个划分

那么贝叶斯公式如下：

                                                

其中 为后验概率， 为先验概率， 为条件概率。

贝叶斯决策就是利用贝叶斯理论进行决策分类，举个最简单的例子，假设有一组细胞，细胞分为正常细胞（ 类）和异常细胞（ 类），所以 。 和 称为先验概率，目前有几种特征（ ），我们依据这几种特征来分析出哪些是正常细胞哪些是异常细胞，所以我们其实就是要算出 和 的大小，然后哪一个概率大就判定为哪一类细胞。结合贝叶斯公式，我们可以知道：

                                                

通过这个式子，我们可以看出，本来直接求 的问题转换成了求解 和 的问题，而这两个概率我们可以根据对训练集做统计就可以求出来。

    三 朴素贝叶斯进行垃圾邮件分类

接下来通过一个例子来说明怎么用朴素贝叶斯来进行垃圾邮箱的分类，首先我们以一个小的数据集为例，先说明算法的分类过程，之后再在一个大一点的数据集上说明如何对数据做交叉验证。

    3.1构造数据集

def loadDataSet():

    '''

    创建数据集

    :return: postingList:样本集  classVec：每个样本对应的标签

    '''

    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],

                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],

                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],

                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],

                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],

                 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]

    classVec = [0,1,0,1,0,1]    #1 is abusive, 0 not

    return postingList,classVec

    3.2 构造词典

    读取了数据集之后，需要构造一个词典，这个词典在之后求解条件概率的时候会用到，这个词典中存储的是在样本集中总共出现了哪些单词。

def getWordVentor(dataSet):

    '''

    根据数据集获取数据集中的不重复单词集，返回词典

    :param dataSet: 训练集

    :return: returnVector : 词典

    '''

    returnVector = set([])

    for line in dataSet:

        returnVector = returnVector | set(line)

    return list(returnVector)

    3.3 构造词集模型

    有了词典之后，我们需要对样本集进行一次处理，需要把单词转换成0/1的集合，0表示该单词在当前样本中未出现，1表示该单词在当前样本出现。这种模型称为词集模型，还有一种模型称为词袋模型，两者不同的地方在于词袋模型统计的是该单词在样本集中出现的次数。

def getVectorFromWords(wordVector, inputWord):

    '''

    把输入的样本替换成0/1的向量

    :param wordVector: 词典

    :param inputWord: 输入的一个样本

    :return: 该样本的词集模型

    '''

    returnVector = [0]*len(wordVector)

    for word in inputWord:

        if word not in wordVector:

            print("this word is not in word vector : %s" %word)

        else:

            returnVector[wordVector.index(word)] = 1

    return returnVector

    3.4 求解先验概率和条件概率

# 获取每个单词在每个类别下的条件概率

# 入参：dataSet : 训练集转换成的词向量矩阵

# 入参：classVec : 每个样本的类别标签

def getProinCLass(dataSet, classVec):

    #先算P(Ci)，即在训练集下，样本是类别1的概率

    numberOfClass1 = sum(classVec)

    Pc1 = float(numberOfClass1/len(dataSet))    #类别1出现的概率

    Pw_C1 = np.ones(len(dataSet[0]))           #类别1中每个单词出现的次数

    Pw_C0 = np.ones(len(dataSet[0]))           #类别0中每个单词出现的次数

    numberWordOfClass1 = 2                      #类别1中出现的单词总数

    numberWordOfClass0 = 2                      #类别0中出现的单词总数



    for i in range(len(dataSet)):

        if classVec[i] == 1:

            Pw_C1 += dataSet[i] #类别1中每个单词出现的次数

            numberWordOfClass1 += sum(dataSet[i]) #类别1中出现的单词总数

        else:

            Pw_C0 += dataSet[i] #类别0中每个单词出现的次数

            numberWordOfClass0 += sum(dataSet[i]) #类别0中出现的单词总数



    #返回P(W|C1)

    PW_C1 = np.log(Pw_C1 / numberWordOfClass1)   #为了防止很多小的数相乘而造成下溢，因此套一层log

    PW_C0 = np.log(Pw_C0 / numberWordOfClass0)

    return PW_C1, PW_C0, Pc1

    3.5 对样本集进行分类

         根据贝叶斯公式，在上一步中计算得到了先验概率和条件概率之后，就可以算出后验概率，也就是根据给定的特征该样本属于哪一类的概率。在做运算的时候，为了防止小的数太多而导致相乘造成下溢，所以进行了取对数操作，所以看到最后的结果概率值不在0-1之间，是因为取了对数值导致的，但是这并不影响我们比对哪一个概率比较大。

# 训练测试样本集

def testTrainDataSet():

    # 拉取数据集

    dataSet, classVec = loadDataSet()

    # 获取词典

    wordVector = getWordVentor(dataSet)

    # 转换成词向量

    trainWordVector = np.zeros(shape=(len(dataSet), len(wordVector)))

    for i in range(len(dataSet)):

        vec = getVectorFromWords(wordVector, dataSet[i])

        trainWordVector[i] = vec

    #获取每个单词的条件概率

    PW_C1, PW_C0, Pc1 = getProinCLass(trainWordVector, classVec)

    return PW_C1, PW_C0, Pc1, wordVector





# 分类测试样本

def testTestingDataSet(testDataSet):

    PW_C1, PW_C0, Pc1, wordVector = testTrainDataSet()

    vec = getVectorFromWords(wordVector, testDataSet)

    PW_C1 = sum(PW_C1*vec) + math.log(Pc1)

    PW_C0 = sum(PW_C0 * vec) + math.log(1-Pc1)

    print("属于第1类的概率",PW_C1)

    print("属于第0类的概率",PW_C0)

    3.6 交叉验证

    我们目前只有训练集的样本数据，如果我们想要测试算法在执行分类的时候的错误率有多大，我们可以用交叉验证的方法，思路就是从训练集中随机取出一部分数据作为测试集，剩下的作为训练集，我们用训练集来训练我们的算法，然后用测试集去测试分类的结果，将算法的分类结果与实际的类别标签进行比对，然后算出错误率。

    目前有一个邮件的数据集，我们使用朴素贝叶斯来进行垃圾邮件的分类，email文件夹下有两个文件夹，ham下的是类别0，即非垃圾邮件，spam下的是类别1，即垃圾邮件。在下面的代码中，我们从50个训练样本中随机抽取出10个作为测试集进行交叉验证。

def loadData():
    '''
    加载email文件夹下面的所有ham和spam文件
    ham下面的样本为0类别
    spam下面的样本为1类别
    :return: 样本集，标签集
    '''
    trainWordsList = [] #训练集词集
    classVector = []    #训练集中每一份文档的类别
    for i in range(1,26):
        curWordList = textParse(open("email/ham/%d.txt" %i).read())
        trainWordsList.append(curWordList)
        classVector.append(0)
        curWordList = textParse(open("email/spam/%d.txt" % i).read())
        trainWordsList.append(curWordList)
        classVector.append(1)
    return trainWordsList, classVector

def spamTest():
    '''
    在测试集中选择一部分数据进行交叉验证
    '''
    # 1.加载数据
    trainWordsList, classVector = loadData()
    # 2.生成词典
    wordDirectory = getWordVentor(trainWordsList)
    #转换成词集模型
    wordSetVector = []
    for i in range(len(trainWordsList)):
        wordSetVector.append(getVectorFromWords(wordDirectory, trainWordsList[i]))
    # 3.从50个测试样本集中随机抽取出10个样本
    trainSet = range(50)
    testSetVector = [] # 测试集样本， 其中存储的是测试集的词集模型
    testSetLabels = [] # 测试集的类别标签，用于后面检验分类的结果
    for i in range(10):
        randomNum = int(np.random.uniform(0, len(wordSetVector), 1)) # numpy中的均匀分布中进行采样
        print("当前随机数为：%f" %randomNum)
        testSetVector.append(wordSetVector[randomNum])
        testSetLabels.append(classVector[randomNum])
        #添加完之后在测试集中删除掉这一条
        wordSetVector.__delitem__(randomNum)
        classVector.__delitem__(randomNum)
    # 4.将剩下的40个测试集转换成词典模型
    print ("训练集的个数为：%d, 测试集的个数为：%d" %(len(wordSetVector),len(testSetVector)))
    print(wordSetVector)
    # 5.训练训练集样本，得到每一个单词为类别1时的概率
    PW_C1, PW_C0, Pc1 = getProinCLass(wordSetVector, classVector)
    print("每个单词为类别1的概率:")
    print(PW_C1)
    # 6.测试10个测试集，用NB进行分类
    testSetCalLabels = []
    for i in range(len(testSetVector)):
        #curVec = testSetVector[i] | PW_C1
        class1Pro = sum(testSetVector[i]*PW_C1)+math.log(Pc1)
        class0Pro = sum(testSetVector[i]*PW_C0) + math.log(1-Pc1)
        if class1Pro > class0Pro:
            testSetCalLabels.append(1)
        else:
            testSetCalLabels.append(0)
        print("当前测试样本的分类标签为：%d" %testSetCalLabels[i])
    # 7.检验分类结果，输出出错率
    errCount = 0
    for i in range(len(testSetCalLabels)):
        if testSetCalLabels[i] != testSetLabels[i]:
            print("第%d个测试样本分类错误" %i)
            errCount += 1
    print("分类错误率为: %f" %(errCount/10))

    四 整体代码实现

'''
created by xiebo
2019.2.28
'''

import numpy as np
import math

def loadDataSet():
    '''
    创建数据集
    :return: postingList:样本集  classVec：每个样本对应的标签
    '''
    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0,1,0,1,0,1]    #1 is abusive, 0 not
    return postingList,classVec


def getWordVentor(dataSet):
    '''
    根据数据集获取数据集中的不重复单词集，返回词典
    :param dataSet: 训练集
    :return: returnVector : 词典
    '''
    returnVector = set([])
    for line in dataSet:
        returnVector = returnVector | set(line)
    return list(returnVector)


def getVectorFromWords(wordVector, inputWord):
    '''
    把输入的样本替换成0/1的向量
    :param wordVector: 词典
    :param inputWord: 输入的一个样本
    :return: 该样本的词集模型
    '''
    returnVector = [0]*len(wordVector)
    for word in inputWord:
        if word not in wordVector:
            print("this word is not in word vector : %s" %word)
        else:
            returnVector[wordVector.index(word)] = 1
    return returnVector

# 把输入的样本替换成词袋模型
# 入参：wordVector : 词典
# 入参：inputWord : 输入的一句话
# 出参: returnVector : 词袋模型
def getVectorFromWords(wordVector, inputWord):
    returnVector = [0]*len(wordVector)
    for word in inputWord:
        if word not in wordVector:
            print("this word is not in word vector : %s" %word)
        else:
            returnVector[wordVector.index(word)] += 1
    return returnVector

# 获取每个单词在每个类别下的条件概率
# 入参：dataSet : 训练集转换成的词向量矩阵
# 入参：classVec : 每个样本的类别标签
def getProinCLass(dataSet, classVec):
    #先算P(Ci)，即在训练集下，样本是类别1的概率
    numberOfClass1 = sum(classVec)
    Pc1 = float(numberOfClass1/len(dataSet))    #类别1出现的概率
    Pw_C1 = np.ones(len(dataSet[0]))           #类别1中每个单词出现的次数
    Pw_C0 = np.ones(len(dataSet[0]))           #类别0中每个单词出现的次数
    numberWordOfClass1 = 2                      #类别1中出现的单词总数
    numberWordOfClass0 = 2                      #类别0中出现的单词总数

    for i in range(len(dataSet)):
        if classVec[i] == 1:
            Pw_C1 += dataSet[i] #类别1中每个单词出现的次数
            numberWordOfClass1 += sum(dataSet[i]) #类别1中出现的单词总数
        else:
            Pw_C0 += dataSet[i] #类别0中每个单词出现的次数
            numberWordOfClass0 += sum(dataSet[i]) #类别0中出现的单词总数

    #返回P(W|C1)
    PW_C1 = np.log(Pw_C1 / numberWordOfClass1)   #为了防止很多小的数相乘而造成下溢，因此套一层log
    PW_C0 = np.log(Pw_C0 / numberWordOfClass0)
    return PW_C1, PW_C0, Pc1

# 训练测试样本集
def testTrainDataSet():
    # 拉取数据集
    dataSet, classVec = loadDataSet()
    # 获取词典
    wordVector = getWordVentor(dataSet)
    # 转换成词向量
    trainWordVector = np.zeros(shape=(len(dataSet), len(wordVector)))
    for i in range(len(dataSet)):
        vec = getVectorFromWords(wordVector, dataSet[i])
        trainWordVector[i] = vec
    #获取每个单词的条件概率
    PW_C1, PW_C0, Pc1 = getProinCLass(trainWordVector, classVec)
    return PW_C1, PW_C0, Pc1, wordVector


# 分类测试样本
def testTestingDataSet(testDataSet):
    PW_C1, PW_C0, Pc1, wordVector = testTrainDataSet()
    vec = getVectorFromWords(wordVector, testDataSet)
    PW_C1 = sum(PW_C1*vec) + math.log(Pc1)
    PW_C0 = sum(PW_C0 * vec) + math.log(1-Pc1)
    print("属于第1类的概率",PW_C1)
    print("属于第0类的概率",PW_C0)


# 将输入的文本拆分成单词集
def textParse(inputString):
    import re
    splitWordList = re.split('\W+', inputString)
    #print(splitWordList)
    return [word.lower() for word in splitWordList if len(word) > 2] #单词长度少于2的过滤掉

# 加载email文件夹下面的所有ham和spam文件
def loadData():
    trainWordsList = [] #训练集词集
    classVector = []    #训练集中每一份文档的类别
    for i in range(1,26):
        curWordList = textParse(open("email/ham/%d.txt" %i).read())
        trainWordsList.append(curWordList)
        classVector.append(0)
        curWordList = textParse(open("email/spam/%d.txt" % i).read())
        trainWordsList.append(curWordList)
        classVector.append(1)
    return trainWordsList, classVector

# 在测试集中选择一部分数据进行交叉验证
def spamTest():
    # 1.加载数据
    trainWordsList, classVector = loadData()
    # 2.生成词典
    wordDirectory = getWordVentor(trainWordsList)
    #转换成词集模型
    wordSetVector = []
    for i in range(len(trainWordsList)):
        wordSetVector.append(getVectorFromWords(wordDirectory, trainWordsList[i]))
    # 3.从50个测试样本集中随机抽取出10个样本
    trainSet = range(50)
    testSetVector = [] # 测试集样本， 其中存储的是测试集的词集模型
    testSetLabels = [] # 测试集的类别标签，用于后面检验分类的结果
    for i in range(10):
        randomNum = int(np.random.uniform(0, len(wordSetVector), 1)) # numpy中的均匀分布中进行采样
        print("当前随机数为：%f" %randomNum)
        testSetVector.append(wordSetVector[randomNum])
        testSetLabels.append(classVector[randomNum])
        #添加完之后在测试集中删除掉这一条
        wordSetVector.__delitem__(randomNum)
        classVector.__delitem__(randomNum)
    # 4.将剩下的40个测试集转换成词典模型
    print ("训练集的个数为：%d, 测试集的个数为：%d" %(len(wordSetVector),len(testSetVector)))
    print(wordSetVector)
    # 5.训练训练集样本，得到每一个单词为类别1时的概率
    PW_C1, PW_C0, Pc1 = getProinCLass(wordSetVector, classVector)
    print("每个单词为类别1的概率:")
    print(PW_C1)
    # 6.测试10个测试集，用NB进行分类
    testSetCalLabels = []
    for i in range(len(testSetVector)):
        #curVec = testSetVector[i] | PW_C1
        class1Pro = sum(testSetVector[i]*PW_C1)+math.log(Pc1)
        class0Pro = sum(testSetVector[i]*PW_C0) + math.log(1-Pc1)
        if class1Pro > class0Pro:
            testSetCalLabels.append(1)
        else:
            testSetCalLabels.append(0)
        print("当前测试样本的分类标签为：%d" %testSetCalLabels[i])
    # 7.检验分类结果，输出出错率
    errCount = 0
    for i in range(len(testSetCalLabels)):
        if testSetCalLabels[i] != testSetLabels[i]:
            print("第%d个测试样本分类错误" %i)
            errCount += 1
    print("分类错误率为: %f" %(errCount/10))


testTestingDataSet(['my', 'love'])

 

    五 参考材料

1.《机器学习实战》Peter Harrington

2. 先验概率和后验概率理解 https://blog.csdn.net/qq_30638831/article/details/83660559

3. 贝叶斯决策理论之入门篇 https://blog.csdn.net/zjy_snow/article/details/82592718