吴恩达机器学习课后作业——神经网络

一、神经网络前向传播

一、作业内容

在上一章的练习中，实现了多类逻辑回归来识别手写数字。但是逻辑回归只是一个线性分类器，不能形成更复杂的假设。神经网络将能够表示形成非线性假设的复杂模型。我们将使用已经训练过的神经网络的参数，实现使用前馈传播算法来对我们的权值进行预测。在这部分练习中，我们将使用与前面多类逻辑回归来识别手写数字相同的训练集实现一个神经网络来识别手写数字。
数据集下载位置(包含吴恩达机器学课后作业全部数据集)：data

二、作业分析

1、在上一章的练习中，实现了多类逻辑回归来识别手写数字。但是逻辑回归只是一个线性分类器，不能形成更复杂的假设。当决策边界明显不是直线的时候，我们就需要使用高阶的多项式去绘制决策边界，但是当特征的数量不断增大，那么计算量也会随之增大。因此，简单的逻辑回归算法并不适合在特征n很大的情况下学习复杂的非线性假设。而神经网络则是学习复杂的非线性假设的一种好办法。

2、在一个神经网络里，我们将会使用一个很简单的模型来模拟神经元工作的过程，将神经元模拟成一个逻辑单元。我们称这个逻辑单元（logistic unit）是一个带激活函数的人工神经元（artificial neuron）。在激活函数中的参数又叫模型的权重(我们在之前的学习中称为参数的θ)。

3、在神经网络中，激活函数是指待非线性函数g(z)，例如我们在简单逻辑回归中的g(z)一样。

4、神经网络中的第一层被称为输入层，最后一层被称为输出层，中间层次则都被称为隐藏层。通常我们会给输入层中加入一个额外的节点$x_0$，这个结点有时也被称为偏执单元或偏执神经元，但$x_0$总是等于1。

5、前向传播：从输入单元的激活项开始，然后进行前向传播给隐藏层，计算隐藏层的激活项，继续进行前向传播，并计算输出层的激活项。

输入特征值$x_i$，$a^1$=$x_i$，$a^2$=g(${\theta }^1$$a^1$), 激活项$a^j$=g(${\theta }^i$$a^i$)，每一层重复此过程，直到得到预测值。

三、代码实战

引入所需函数库

import numpy as np
import scipy.io as scio

定义sigmoid函数

def sigmoid(z):
    return 1/(1 + np.exp(-z))

前向传播函数

def forwardPropagation(X, y, theta1, theta2):
    # a1 = xi
    a1 = X
    #进行第一层传播，得到25*5000的a2
    # 运算符@在矩阵运算中的功能是矩阵乘法
    a2 = sigmoid(theta1@a1.T)
    # 为a2添加偏置单元
    a2 = np.insert(a2, 0, values=1, axis=0)
    # 进行第二层传播得到一个10*5000的a3输出层
    a3 = a2 = sigmoid(theta2@a2)
    return a3

加载数据并导入权重

# 导入训练集
data = scio.loadmat('ex3data1.mat')
X = data['X']
y = data['y']
# 导入权重
weights = scio.loadmat('ex3weights.mat')
theta1 = weights['Theta1']
theta2 = weights['Theta2']
# 插入一列1作为偏置单元
# axis等于0时按行插入，等于1时按列插入
X = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1)

进行精度预测

# 进行精度预测
a3 = forwardPropagation(X, y, theta1, theta2)
# 因为是多元分类，因此这里需要选择每一个样本在训练集中的最大的分类器
prediction = np.argmax(a3, axis=0) + 1
# 将真值y从2维数据缩减成1维数据
y = y.flatten()
# 输出精度
print('accuary', np.mean(y == prediction)*100, '%')

输出结果

accuary 97.52 %

二、正则化逻辑回归

一、作业内容

在本练习的前一部分中，实现了神经网络的前向传播识别手写数字。在这部分练习中，我们将实现反向传播的前馈神经网络再次处理手写数字数据集。我们将通过反向传播算法实现神经网络成本函数和梯度计算的非正则化和正则化版本。 我们还将实现随机权重初始化和使用网络进行预测的方法。

二、作业分析

1、BP算法(即误差反向传播算法)适合于多层神经元网络的一种学习算法，它建立在梯度下降法的基础上。BP网络的输入输出关系实质上是一种映射关系：一个n输入m输出的BP神经网络所完成的功能是从n维欧氏空间向m维欧氏空间中一有限域的连续映射，这一映射具有高度非线性。它的信息处理能力来源于简单非线性函数的多次复合，因此具有很强的函数复现能力。这是BP算法得以应用的基础。

2、反向传播算法主要由两个环节(激励传播、权重更新)反复循环迭代，直到网络的对输入的响应达到预定的目标范围为止。

BP算法的学习过程由正向传播过程和反向传播过程组成。在正向传播过程中，输入信息通过输入层经隐含层，逐层处理并传向输出层。如果在输出层得不到期望的输出值，则取输出与期望的误差的平方和作为目标函数，转入反向传播，逐层求出目标函数对各神经元权值的偏导数，构成目标函数对权值向量的梯量，作为修改权值的依据，网络的学习在权值修改过程中完成。误差达到所期望值时，网络学习结束。

3、激励传播：
每次迭代中的传播环节包含两步：
(1) (前向传播阶段)将训练输入送入网络以获得激励响应；
(2) (反向传播阶段)将激励响应同训练输入对应的目标输出求差，从而获得隐层和输出层的响应误差。

4、权重更新
对于每个突触上的权重，按照以下步骤进行更新：
(1) 将输入激励和响应误差相乘，从而获得权重的梯度。
(2) 将这个梯度乘上一个比例并取反后加到权重上。
(3) 这个比例将会影响到训练过程的速度和效果，因此称为“训练因子”。梯度的方向指明了误差扩大的方向，因此在更新权重的时候需要对其取反，从而减小权重引起的误差。

5、反向传播更新计算中代价函数的计算公式：

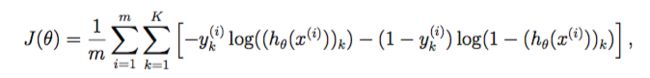
6、反向传播函数中，误差的计算过程：
${\delta }_j^3$=$a_j^3$-$y_j$
${\delta }_j^2$=$($${\Theta }^2$${)}^T$${\delta }^3$*g’($z^2$)
注意：
(1) 首先我们要定义一个${\delta }_j^l$，它代表第l层中第j个节点的误差值

(2) 然后因为我们通过训练集是可以知道真实值y的，因此输出层的误差是可以直接计算出来的，也就是${\delta }_j^3$=$a_j^3$-$y_j$ 。 并且我们可以写成向量形式，从而得到${\delta }^3$=$a^3$-y

(3) 然后我们进一步可以得到${\delta }^2$，根据上面的公式计算即可。并且我们对公式进一步展开，还可以得到g’($z^2$)=$a^2$(1-$a^2$)

(4) 需要注意的是，我们是不用计算${\delta }^1$的，因为输入层是没有误差的

(5) 最后，我们就可以得到偏导数。

7、求偏导数之和的均值

注意：
$(1)$${\Delta }_i$${}_j^l$其实是δ的大写形式，是用来求每一个样本的J(θ)对于$:$${\theta }_i$${}_j^l$的偏导数之和，然后最后再取一个均值，也就是最后$:$$D_i$${}_j^l$中除以m

8、One-Hot 编码
One-Hot编码：又称为一位有效编码，主要是采用N位状态寄存器来对N个状态进行编码，每个状态都由他独立的寄存器位，并且在任意时候只有一位有效。

One-Hot编码是分类变量作为二进制向量的表示。这首先要求将分类值映射到整数值。然后，每个整数值被表示为二进制向量，除了整数的索引之外，它都是零值，它被标记为1。

假设对于学生的性别【男，女】进行编码
根据上面的官方概念，采用 N 位状态寄存器对 N 个状态进行编码，这里的特征有2个，也就是 N = 2，所以可以有下面的表示方式：
男 → [1, 0] ；
女 → [0, 1] ；

假设对于学生的年级【小学，初中，高中】进行编码
如上，可以有如下表示：
小学 → [1, 0, 0] ；
初中 → [0, 1, 0] ；
高中 → [0, 0, 1] ；

假设对于学生的特长【钢琴，绘画，舞蹈，篮球】进行编码
如上，可以有如下表示：
钢琴 → [1, 0, 0, 0,] ；
绘画 → [0, 1, 0, 0] ；
舞蹈 → [0, 0, 1, 0] ；
篮球 → [0, 0, 0, 1] ；

那么，如果是这样的一个样本 【男，初中，篮球】，就可以这么表示：[1, 0, 0, 1, 0, 0, 0, 0, 1] 。

详情可见：https://blog.csdn.net/weixin_41857483/article/details/111396939

三、代码实战

引入所需函数库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat

加载数据并进行数据预处理

# 加载数据
data = loadmat('ex4data1.mat')
X = data['X']
y = data['y']

# 对y标签进行一次one-hot编码
# one-hot 编码将类标签n（k类）转换为长度为k的向量，其中索引n为“hot”（1），而其余为0
encoder = OneHotEncoder(sparse=False)
y_onehot = encoder.fit_transform(y)

创建sigmoid 函数

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

创建前向传播函数

# 前向传播函数
# (400 + 1) --> (25 + 1) --> (10)
def forward_propagate(X, theta1, theta2):
    m = X.shape[0]

    a1 = np.insert(X, 0, values=np.ones(m), axis=1)
    z2 = a1 * theta1.T
    a2 = np.insert(sigmoid(z2), 0, values=np.ones(m), axis=1)
    z3 = a2 * theta2.T
    h = sigmoid(z3)

    return a1, z2, a2, z3, h

首先我们要创建评估一组给定的网络参数的损失的代价函数

# 代价函数
def cost(params, input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]
    X = np.matrix(X)
    y = np.matrix(y)

    # 将参数数组重新塑造为每一层的参数矩阵
    theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))

    # 运行向前传播函数
    a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)

    # 计算代价函数
    J = 0
    for i in range(m):
        first_term = np.multiply(-y[i, :], np.log(h[i, :]))
        second_term = np.multiply((1 - y[i, :]), np.log(1 - h[i, :]))
        J += np.sum(first_term - second_term)

    J = J / m

    return J

然后我们在该代价函数的基础上增加代价函数的正则化
正则化术语只是我们已经计算出的代价的一个补充

# 正则化代价函数
def cost(params, input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]
    X = np.matrix(X)
    y = np.matrix(y)

    # 将参数数组重新塑造为每一层的参数矩阵
    theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))

    # 运行向前传播函数
    a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)

    # 计算代价函数
    J = 0
    for i in range(m):
        first_term = np.multiply(-y[i, :], np.log(h[i, :]))
        second_term = np.multiply((1 - y[i, :]), np.log(1 - h[i, :]))
        J += np.sum(first_term - second_term)

    J = J / m

    # 加上正则化项
    J += (float(learning_rate) / (2 * m)) * (np.sum(np.power(theta1[:, 1:], 2)) + np.sum(np.power(theta2[:, 1:], 2)))

    return J

接下来是反向传播算法。 反向传播参数更新计算将减少训练数据上的网络误差。
我们需要的第一件事是计算我们之前创建的Sigmoid函数的梯度的函数。

# 计算sigmoid函数的梯度
# 用于计算sigmoid函数的导数值
def sigmoid_gradient(z):
    return np.multiply(sigmoid(z), (1 - sigmoid(z)))

现在我们准备好实施反向传播来计算梯度。 由于反向传播所需的计算是代价函数中所需的计算过程，所以我们将在原正则化代价函数的基础上扩展代价函数以执行反向传播并返回代价和梯度。并将梯度计算也正则化

# 反向传播算法
# 扩展代价函数以执行反向传播并返回代价和梯度
def backprop(params, input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]
    X = np.matrix(X)
    y = np.matrix(y)
    # 将参数数组重新塑造为每一层的参数矩阵
    theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))

    # 运行feed-forward pass
    a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)

    # 初始化
    J = 0
    delta1 = np.zeros(theta1.shape)     #  (25, 401)
    delta2 = np.zeros(theta2.shape)     #  (10, 26)

    # 计算代价函数
    for i in range(m):
        first_term = np.multiply(-y[i, :], np.log(h[i,:]))
        second_term = np.multiply((1 - y[i, :]), np.log(1 - h[i,:]))
        J += np.sum(first_term - second_term)

    J = J / m

    # 加上正则化项
    J += (float(learning_rate) / (2 * m)) * (np.sum(np.power(theta1[:,1:], 2)) + np.sum(np.power(theta2[:,1:], 2)))

    # 执行反向传播
    for t in range(m):
        a1t = a1[t,:]  # (1, 401)
        z2t = z2[t,:]  # (1, 25)
        a2t = a2[t,:]  # (1, 26)
        ht = h[t,:]  # (1, 10)
        yt = y[t,:]  # (1, 10)

        d3t = ht - yt  # (1, 10)

        z2t = np.insert(z2t, 0, values=np.ones(1))  # (1, 26)
        d2t = np.multiply((theta2.T * d3t.T).T, sigmoid_gradient(z2t))  # (1, 26)

        delta1 = delta1 + (d2t[:, 1:]).T * a1t
        delta2 = delta2 + d3t.T * a2t

    delta1 = delta1 / m
    delta2 = delta2 / m

    # 加上梯度正则化项
    delta1[:,1:] = delta1[:,1:] + (theta1[:,1:] * learning_rate) / m
    delta2[:,1:] = delta2[:,1:] + (theta2[:,1:] * learning_rate) / m

    # 将梯度矩阵分解为单个数组
    grad = np.concatenate((np.ravel(delta1), np.ravel(delta2)))

    return J, grad

准备执行反向传播函数时需要用到的一些数据

# 初始化设置
# 首先要确定输入层和输出层的单元数
input_size = 400
hidden_size = 25
num_labels = 10
learning_rate = 1

# 随机初始化完整网络参数大小的参数数组
# 通常我们会把权重初始化为很小的值，接近于0
params = (np.random.random(size=hidden_size * (input_size + 1) + num_labels * (hidden_size + 1)) - 0.5) * 0.25

m = X.shape[0]
X = np.matrix(X)
y = np.matrix(y)

# 将参数数组解开为每个层的参数矩阵
theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))

使用反向传播，获得最优参数

from scipy.optimize import minimize

fmin = minimize(fun=backprop, x0=params, args=(input_size, hidden_size, num_labels, X, y_onehot, learning_rate), method='TNC', jac=True, options={'maxiter': 250})

由于目标函数不太可能完全收敛，我们对迭代次数进行了限制。 我们的总代价已经下降到0.5以下，这是算法正常工作的一个很好的指标。 让我们使用它发现的参数，并通过网络转发，以获得一些预测。

print(fmin)

结果：

     fun: 0.3215671250858979
     jac: array([-6.45900863e-05,  2.09605604e-07,  6.49231619e-07, ...,
       -6.24230480e-05, -4.88014479e-05,  2.57309040e-05])
 message: 'Max. number of function evaluations reached'
    nfev: 250
     nit: 22
  status: 3
 success: False
       x: array([-1.14966018e-01,  1.04802802e-03,  3.24615810e-03, ...,
       -2.80888495e+00, -2.13875212e+00, -6.24569360e-01])

让我们使用它找到的参数，并通过网络前向传播以获得预测

# 通过网络前向传播以获得预测
X = np.matrix(X)
theta1 = np.matrix(np.reshape(fmin.x[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
theta2 = np.matrix(np.reshape(fmin.x[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))

a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
y_pred = np.array(np.argmax(h, axis=1) + 1)

最后，我们可以计算准确度，看看我们训练完毕的神经网络效果怎么样

# 计算准确度
correct = [1 if a == b else 0 for (a, b) in zip(y_pred, y)]
accuracy = (sum(map(int, correct)) / float(len(correct)))
print ('accuracy = {0}%'.format(accuracy * 100))

结果：

accuracy = 99.38%

总结：
建神经网络的整体架构的步骤：

1、对初始数据进行预处理，以满足各函数计算的需求
(1) 对y标签进行一次one-hot编码。 one-hot 编码将类标签n（k类）转换为长度为k的向量，其中索引n为“hot”(1)，而其余为0。

(2) 确定输入层和输出层的单元数。较为合理的默认选择是只有一层隐藏层，如果有多个隐藏层，那么每个隐藏层的单元数最好相同（虽然更多的单元数会得到更好的结果，但是也要考虑到计算量）。隐藏层的单元数还应该和输入层的单元数相匹配，可以是1倍、2倍、3倍4倍等。

(3) 随机初始化完整网络参数大小的参数数组，也就是随机初始化权重。通常我们会把权重初始化为很小的值，接近于0。

(4) 将X和y转换为可以用于矩阵计算的格式

(5) 将参数数组解开为每个层的参数矩阵

2、评估一组给定的网络参数的损失的代价函数。反向传播参数更新计算将减少训练数据上的网络误差并返回代价和梯度。

3、在反向传播函数经过一定次数的迭代之后，将总代价下降到0.5以下。

4、使用反向传播函数得到的参数，通过网络前向传播以获得预测。

参考链接：https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
https://blog.csdn.net/weixin_41799019/article/details/117324623?spm=1001.2014.3001.5502