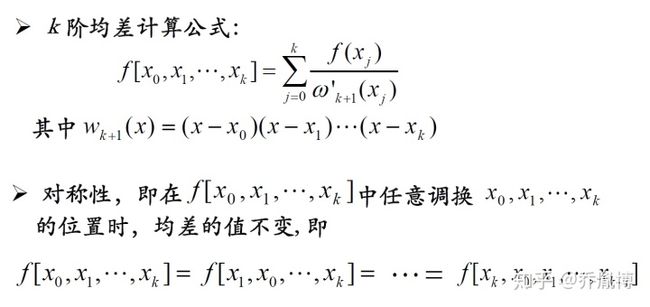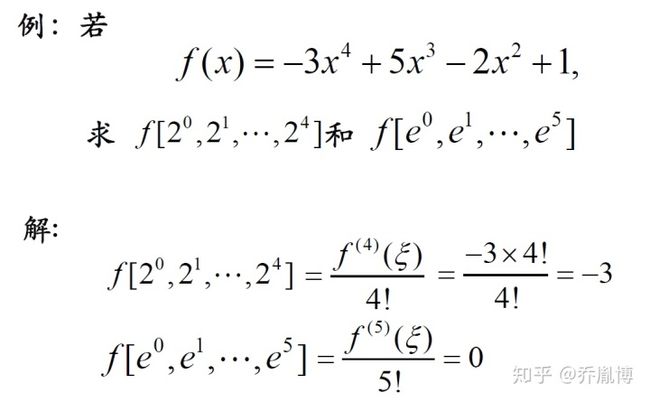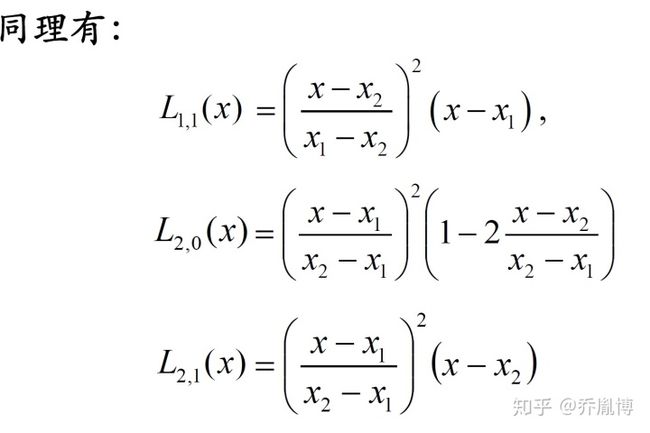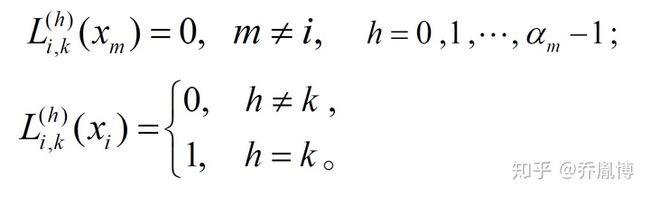多项式的拟合与插值例题_矩阵与数值计算(12)——Lagrange插值、Newton插值、Hermite插值...
前言
接下来的主要内容是与插值逼近相关的内容。科学计算中的许多问题需要计算函数
插值方法是数值分析中一个简单而又重要的方法,利用该方法可以通过函数在有限点处的函数值求出其近似函数,进而夫算出函数在其他点处的值。插值方法在离散数据处理、函数的近似表示、数值微分、数值积分、曲线与曲面的生成等方面有重要作用。
下面我们先介绍插值的基本定义和插值格式,再介绍三种多项式插值方法,分别是Lagrange(拉格朗日)插值、Newton(牛顿)插值和Hermite插值。
一、引言
问题描述,面对给定的点和相关函数的信息,我们要估计未给出点的函数值,就需要使用到插值方法,
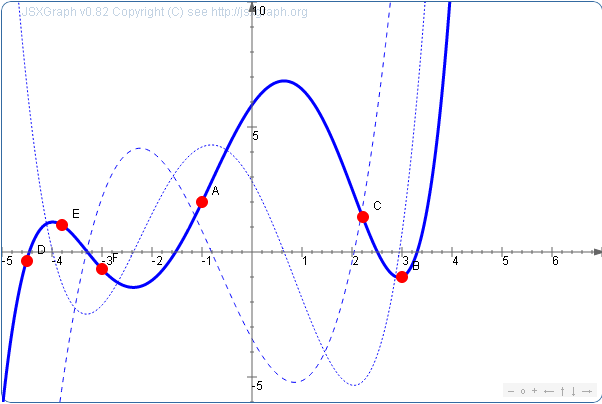
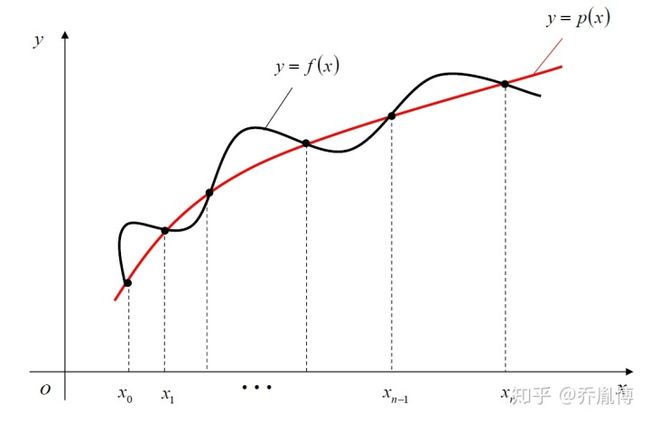
问题描述从几何上来理解,如下图所示
插值几何角度解释p(x)是我们计算出来的对f(x)的拟合函数,并且穿过给定的数据对
基本的思想:
- 简单函数类基底需要满足的条件
- 给出具体的基底
- 给出系数
当我们看到
但是我们都知道,线性方程组不一定有解,需要满足一定的条件,这个条件定义如下,
我们称这个条件为解的存在的Haar条件。
接下来我们就可以定义插值基函数,
上面的假设可以这样理解,插值基函数再我们此时的定义中是未知的,是这样一种假设的形式,我们希望对于每一个已知点
二、Lagrange插值
我们之前已经得到了插值基函数的基本形式,接下来的问题就是解决如何求解
多项式函数显然满足Haar条件,这样我们就可以利用插值的方法来解决问题,并且解是唯一的。
正如上面所说的,我们完全可以利用线性方程组来求解系数,但是非常困难,涉及很复杂的矩阵分解。这里我们就提出了Largange插值和Newton插值来求解这些系数。
那么我们先介绍Largange插值方法。
构造
由于
下面我们看一道例题来理解一下,
Lagrange插值法计算起来非常的简单便捷,很快我们就能得到问题的精确解,但是我们也发现一个问题。
在插值问题中,为了提⾼插值精度,有时需增加插值节点个数。插值节点个数发⽣变化后,所有的Lagrange插值基函数都会发⽣变化,从⽽整个Lagrange插值多项式的结构发⽣变化,这在计算实践中是不⽅便的。
那么这种问题如何改进和解决呢?
三、Newton插值法
为了克服Lagrange插值多项式的缺点,能灵活地增加插值节点,使其具有“承袭性”,即可以充分利用已有的信息,我们引进Newton插值公式。
查找了一些资料,没有找到非常易懂的从Lagrange到Newton的推导过程,只能自己自力更生,那么这里给出我自己的推导,以供大家深入理解Newton法。
商差是为了便于Newton插值的计算和表达引入的概念,便于我们迭代求解。我们给出商差的严格定义,
商差他有下面几种性质
第三个性质经常会在题目中出现,作为填空和选择题出现。
实际上,至此为止Newton法的基本形式和求解方式已经介绍完毕,我们可以看到实际上Newton插值和Lagrange插值完全是相同的,只是表达形式不同而已。
还是通过两道例题观察一下
这道例题使用到了商差性质3。
考试中可以直接使用均差表来进行计算,Newton插值表达形式。
插值余项
得到Lagrange何Newton插值的求解方法,如何来衡量插值的结果的优劣程度,需要一个指标,我们引入插值余项,来衡量插值与实际真实值之间的差距。
插值余项Lagrange与Newton法使用的都是非导数信息,求解插值表达式,如果给出一些一阶导的条件如何去求出插值表达式呢?
四、Hermite插值
理论和应用中,提出的某些插值问题,要求插值函数
那么我们定义问题,如下所示
要构造满足上述插值条件的插值公式,借鉴的是Lagrange插值公式。
给出构造方法如下所示
Hermite插值公式构造方式当
我们来看两道例题帮助我们观察如何构造Hermite插值多项式。
下面看一个重点要求掌握的,二点三次Hermite插值多项式的构造。
对于二点三次Hermite插值多项式四个系数的推导可以不掌握,但是需要记忆四个系数的求解公式,考试中会考察二点三次Hermite插值的构造。
应该有不少同学有和我一样的疑问,为什么二点Hermite插值结果是三次呢?这个就需要我们重新审视假设条件
假设有这样一个情况
下面简单给出二点三次Hermite的插值余项,
总结
综上我们介绍了多项式插值的基本内容,后续会介绍逼近相关内容。