【IJCAI2020-论文分享】Knowledge Hypergraphs Prediction Beyond Binary Relations（知识表示）

【IJCAI2020-论文分享】Knowledge Hypergraphs Prediction Beyond Binary Relations（知识表示）

目前基于嵌入的知识图谱的表示方式都默认所有的关系为二元关系，但是事实上以Freebase为例，有超过61%的关系是非二元关系。所以论文提出将知识图谱转化为知识超图并提出了HsimplE和Hype两种知识超图嵌入表示的方法。
超图(Hypergraph)：就是每一个边可以包含两个以上的点所构成的图。当每个边所包含的顶点个数都是相容且为K个，就可以被称为K阶超图。

下图是一个三阶超图的示例：每条直线或者曲线代表的是一个超边，每个超边包含3个顶点。

在知识图谱中，使用两个实体之间的关系存储一个知识。作者在论文的工作中讨论了知识超图中的链接预测问题，其中关系是在任意数量的实体上定义的。

知识超图是什么？

知识超图是以任意数量的实体之间的关系形式存储有关事实图形结构的知识库。可以看做是知识图谱的一种变型。

任务：由于记录世界上所有的事实是不可能的，所以知识库是不完整的，需要通过关系预测根据现在已有的关系预测未知的关系。文章中心任务是要预测知识超图中的链接预测问题。

知识图谱的关系预测目前是一个被广泛研究的问题。在这些研究中，通常将知识图谱定义为以节点为实体、以边为关系的有向图，并通过三元组表示，将信息表示为一个二元关系的集合，但是Wen等人观察到，在原始知识图谱【FREEBASE】中，超过1/3的实体参与了非二元关系（比如在超过两个实体间定义的关系），此外，作者还观察到知识图谱中61%的关系是非二元的。

虽然基于嵌入的模型已经被证明是有效的，但是这些方法学习实体和关系的嵌入将所有的关系都假设为二元的。相比之下，知识超图是一个未被充分研究的领域，由于将非二元关系转化为二元关系并进行关系预测的方法并不能产生令人满意的结果。

虽然现在有着将非二元的关系转换为二元关系的技术，例如reification，但是作者发现通过当前这些基于嵌入的方法并不能很好的完成知识图谱的表示任务。所以作者提出了HSimplE和HypE，这两种基于嵌入的方法直接处理知识超图。这两种模型中，预测都是通过关系嵌入、实体嵌入以及在关系中相应位置的函数（没看懂这句话）。同时论文还开发了超图预测的公共数据集、benchmarks和baseline，通过实验证明了所提出的模型比baseline效果更好。

图1a中的示例展示了三个与关系相关的事实，在论文示例中具体化超图时如图1b所示，添加了三个重新定义的实体。在表示方面，创建的二元关系与原始表示等价，并且在转换过程中，重新定位不会丢失信息。但是重新定义这个方法在测试是出现一个问题：因为引入了模型在训练过程中从未遇到过的新实体，因此没有这些实体的学习嵌入，但是目前的方法需要为每个实体嵌入一遍可以做出预测。

图1c将星团（star-to-clique，2019年提出的一种嵌入方法）的方法应用于图1a的结果，其中（加拿大航空公司、纽约、洛杉矶）之间的双重流动可能会被解释为真实的，但是从原始超图来看，加拿大航空公司没有从纽约到洛杉矶的关系。所以星团的方法应用于超图不会产生更好的结果。

由于目前的方法不太实用，所以论文提出了两个基于嵌入的模型，直接对知识超图进行关系预测而不需要将其转换为图。

第一个模型非常简单，对于给定的实体，HSimplE会根据实体在给定关系中的位置来自动嵌入的实体。

第二个模型HypE，除了学习实体嵌入外，还学习位置嵌入，这些位置嵌入从实体表示中分类出来，用于根据实体在关系中的位置转换实体的表示。这使得HypE对元组中实体位置的变化更实用。

为了评估两个模型，作者从知识图谱（FREEBASE）的子集中引入了两个新的数据集，并通过扩展现有的知识图谱模型处理为超图来确定baseline。

符号定义：

E：实体有限集

R：关系有限集

T：元组有限集：【元组的实体属于E，关系属于R】世界中的事实属于T的为TRUE不属于的为false，知识超图由元组T的子集组成。

详细方法：

方法的核心思想是实体表示用于预测的方式受实体在给定关系中所扮演的角色（或位置）的影响。在图1a中的示例中，蒙特利尔是出发城市；但它可能出现在另一个元组中的不同位置（例如到达城市）。这意味着使用蒙特利尔嵌入来计算预测的方式可能需要根据它在元组中的位置而变化。一般来说，当实体的嵌入不依赖于它在元组中的位置时，关系必须是对称的（这不是大多数关系的情况）。另一方面，当实体嵌入是基于位置而独立学习时，一个位置的信息不会与其他位置的信息交互。需要注意的是，在几种基于嵌入的知识图完成方法中，预测依赖于元组中每个实体的位置。

HSimplE：

HSimplE是一种基于嵌入的知识超图链接预测方法，其灵感来自SimplE。SimplE学习实体e的两个嵌入向量e（1）和e（2）（实体的每个可能位置对应一个），以及关系r的两个嵌入向量r（1）和r（2）（其中一个关系嵌入为另一个的逆）。然后计算三元组的分数：

在HSimplE中，采用了根据实体在关系中的位置对其进行不同表示的思想，并从单个训练元组中更新所有这些表示。通过将每个实体e表示为单个向量e（而不是简单的多个向量），将每个关系r表示为单个向量r。从概念上讲，每个e可以视为基于每个可能位置的e的不同表示的串联。例如，在一个知识超图中，与最大数的关系是α，一个实体可以出现在α不同的位置；因此e是α向量的串联，每个可能的位置对应一个。HSimplE使用以下函数对元组进行评分。

HypE：
HypE学习每个实体的一个表示，每个关系的一个表示，以及每个可能位置的位置卷积权重过滤器。当一个实体出现在特定位置时，首先使用适当的位置过滤器来转换给定事实中每个实体的嵌入；然后将这些转换后的实体嵌入与关系的嵌入结合起来生成分数，即输入元组为真的概率。HypE的架构如上图2b和2c所示。
学习从实体嵌入中分离出来的位置过滤器的好处有两个方面：一方面，学习每个实体的单个向量可以使实体表示简单，并且可以从给定事实中的位置分离出来。另一方面，与HSimplE不同，HypE从出现在给定位置的所有实体中学习位置过滤器；总体而言，这种实体、关系和位置表示的分离有助于表示具有任意数量实体的事实的知识库。它还为HypE提供了一个额外的健壮性，比如当作者在一个tuple上测试一个经过训练的HypE模型时，这个元组包含了一个在训练时从未见过的实体。

训练：

两种方法都使用小批量随机梯度下降进行训练。在每次学习迭代中，作者从知识超图中提取一批正元组。由于作者只有正实例可用，所以还需要在负实例上训练模型；因此，对于每个正实例，都生成一组负实例。对于负样本生成，遵循Bordes对知识图的对比方法，并将其扩展到知识超图：对于每个元组，作者通过将元组中的每个实体替换为N个随机实体来生成一组大小为N | r |的负样本。这里，N是训练集中阴性样本的比率，是一个超参数。

作者将知识超图中的元组划分为训练集、验证集和测试集三部分。对于每一个元组都会生成一个负例样本。

作者定义了如下的交叉熵loss函数：

实验：

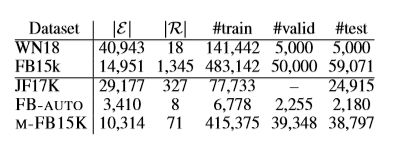
在三个数据集上进行了知识超图完备化的实验。第一个是由Wen等人提出的JF17K。（2016年）；由于JF17K没有提出验证集，作者随机选择20%的训练集作为验证。作者还从FREEBASE创建了两个数据集FB-AUTO和M-FB15K。对于具有二元关系的数据集的实验，使用两个标准基准来完成知识图：WN18[Bordes
et al.，2014]和FB15k[Bordes et
al.，2013]。数据集统计见表2。

为了将结果与现有工作的结果进行比较，作者首先设计了简单的基线，将当前模型扩展到使用知识超图。对于链路预测任务，作者只考虑允许简单扩展到更高二元关系的模型。此任务的基线分为以下几类：（1）处理二元关系且易于扩展到更高arity的方法，即r-SimplE、m-DistMult和m-CP；（2）可以处理更高arity关系的现有方法，即m-TransH。

基于JF17K、FB-AUTO和M-FB15K的基线知识超图完成结果及提出的方法。型号名称中的前缀“r”和“m”分别代表重新定位和多重性。提出的两种方法在所有数据集上都优于基线。

通过学习的位置相关卷积滤波器进行知识共享的能力表明，HypE需要比HSimplE更少的参数来获得良好的结果。为了测试这一点，作者用不同的嵌入维度训练两个模型。图3a显示了不同嵌入尺寸的每个模型在测试集中的MRR。基于MRR结果，可以看到HypE比HSimplE在嵌入维度50时的性能要好24%，这意味着HypE在预算受限的情况下工作得更好。

分离实体嵌入和位置过滤器的表示可以使HypE更好地了解位置在关系中的作用，因为学习过程考虑到在训练时出现在给定位置的所有实体的行为。当某些实体从未出现在训练集的某些位置时，这一点就显得尤为重要，但您仍然希望能够对它们进行推理，而不管它们在证明时间中出现在什么位置。为了在这个更具挑战性的场景中测试作者的模型的有效性，作者通过从原始测试集中选择元组来创建一个缺失位置测试集

至少有一个实体位于它从未出现在训练集中的位置。这些实验的结果（图3B）表明（1）HSimplE和HypE的性能都优于m-CP（它为每个实体位置对学习不同的嵌入），更重要的是，（2）对于这个具有挑战性的测试集，HypE显著优于HSimplE，让我们相信，在这种情况下，分离实体和位置表示可能是更好的策略。

为了证明HSimplE和HypE在更常见的知识图上也能很好地工作，作者在WN18和FB15K上对它们进行了评估。表3显示了WN18和FB15K的链路预测结果。基线结果取自原始论文，除了自己实现的m-TransH。作者没有调整HypE的参数以获得潜在的更好的结果，而是遵循Kazemi和Poole（2018）使用相同的网格搜索方法设置n=2、l=2和s=2。这导致表3中的所有模型都具有相同数量的参数，因此它们可以直接相互比较。注意，对于知识图完成（所有二元关系），HSimplE在理论上和实验上都等价于SimplE（如第4节所示）。结果表明，在WN18和FB15K上，HSimplE和HypE的表现优于所有基线。