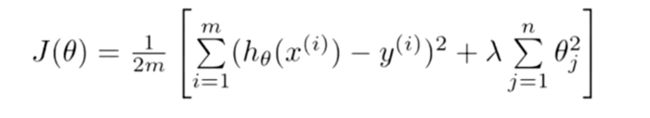机器学习笔记 - 过拟合和正则化

前言

上一篇博客简单总结了机器学习的概念和使用线性回归拟合一条直线。这篇主要介绍如何用线性回归拟合曲线，以及如何解决过拟合问题。

 

基本概念

　　　　　　　　　　　　　　　　　　　　图片来自吴恩达机器学习视频

欠拟合：模型不能很好的描述整个训练集数据。（左图）

过拟合：模型将训练数据中的特例或是误差也进行了描述，导致模型泛化能力差，不能准确预测新样本。（右图）

 

如何拟合曲线

     

如果我们的训练数据只有一个特征，并且特征和标签之间不是线性关系，我们要如何去建立模型呢？下面就来解决这个问题。

1、首先我们生成测试数据。上图的数据是用octave生成的，数据中包含三个特例。下面是生成测试数据的代码：

#生成训练数据
x = linspace(-10, 10, 20);
y = -x.^2 + 2 * x + 1;

#添加噪声
y(5) = y(5) + 50;
y(10) = y(10) - 40; 
y(15) = y(15) + 20;

plot(x, y,'rx', 'MarkerSize', 10);

 

 2、由于特性和标签之间不是线性相关，我们需要把已有的特征做映射，生成更多的特征。以下的代码就是把已有特征映射到1~6次幂。比如一条训练数据输入为2，那么这个函数的作用就是输出2¹，2²，2³ ，... ， 2⁶，和一列偏置量全为1。

function out = mapFeature(X)
  
  #最高次幂
  degree = 6;
  #初始化输出，输出的数据行数和输入一样，但列增多
  #如输入矩阵为 50x1， 那么输出则是 50x7 (第一列为偏置量，全都为1)
  out = ones(size(X(:,1)));
  for i = 1:degree
    out(:, end+1) = X.^i;
  end

end

 

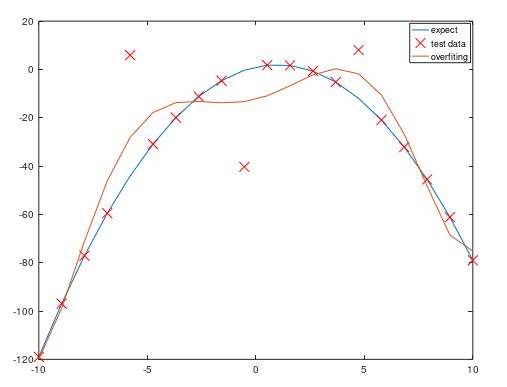
3、使用特征映射得到更多特征后，用得到的数据进行线性回归训练，我们就能得到（左下图）训练结果。可以看出因为有噪音数据的存在，并且模型较为复杂（最高6次幂），因此模型对测试数据拟合过度，可能会导致对新数据预测能力差（泛化误差大）。

比如图中的对特征为0值的预测，现有的模型会得出绿色的X为结果（输出标签大概是-20），而我们期望的结果是黄色的X（输出结果大概是0），预测误差较大。我们如何来解决过拟合问题呢。

 

　

 

正则化（regulation）缓解过拟合问题

   

图中，红色线代表训练模型，而蓝色线代表期望模型；可以看出训练模型明显比期望模型复杂，简化模型就是正则化的思想。为模型的损失函数增加一个复杂度的惩罚项，越复杂的模型受到的惩罚越重，从而达到简化模型的效果。对线性回归的损失函数加上正则化后的公式如下：

 

中括号中的最后一项就是正则项，其中λ表示正则化程度，程序中可作为参数传递。

 

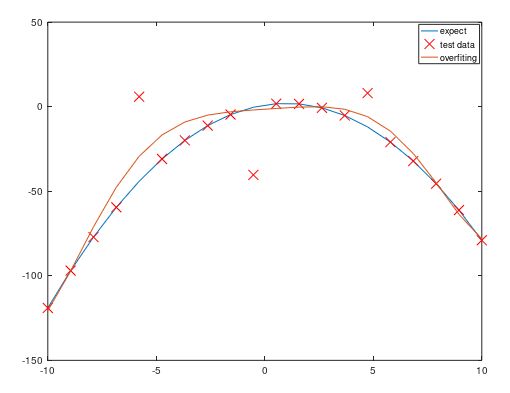
加入正则化后，权重值越大损失函数值越大，这和我们的目标（最小化损失函数）冲突。这样模型就会根据λ在减小模型复杂度和拟合训练数据之前进行折中，在λ选择合适时，我们就能得到一个满意的模型。而λ过大会导致欠拟合问题，过小又会导致过拟合问题。下图是加入正则化之后，训练数据的拟合情况，可以看出训练出的模型变得更加简单了。

  

 

 

Octave代码

 

 1 function out = mapFeature(X)
 2   
 3   #最高次幂
 4   degree = 6;
 5   #初始化输出，输出的数据行数和输入一样，但列增多
 6   #如输入矩阵为 50x1， 那么输出则是 50x7 (第一列为偏置量，全都为1)
 7   out = ones(size(X(:,1)));
 8   for i = 1:degree
 9     out(:, end+1) = X.^i;
10   end
11 
12 end

mapFeature.m

 

 1 function [J, grad] = costFunction(theta, X, y)
 2 
 3 m = length(y); 
 4 
 5 #初始化输出
 6 J = 0;
 7 grad = zeros(size(theta));
 8 
 9 #代价函数
10 J = (1/(2*m)) * sum((X * theta - y)' .^ 2);
11 #梯度
12 grad = (1 / m) * (X' * (X * theta - y));
13 
14 
15 end

costFunction.m

 

 1 clear ; close all; clc;
 2 
 3 #生成训练数据
 4 x = linspace(-10, 10, 20);
 5 y = -x.^2 + 2 * x + 1;
 6 
 7 #希望得到的结果
 8 plot(x, y);
 9 hold on;
10 
11 #添加噪声
12 #y = y + rand(size(y)) * 50;
13 y(5) = y(5) + 50;
14 y(10) = y(10) - 40; 
15 y(15) = y(15) + 20;
16  
17 plot(x, y,'rx', 'MarkerSize', 10);
18 hold on;
19 
20 
21 y = y';
22 x = x';
23 
24 #特征映射，将特征最高映射到6次幂
25 X = mapFeature(x);
26 
27 #获取训练数据数量和特征数量
28 [m, n] = size(X);
29 
30 #训练样本增加偏置量
31 X = [ones(m,1), X];
32 
33 init_theta = zeros(n + 1, 1);
34 
35 #优化算法参数配置
36 options = optimset('GradObj', 'on', 'MaxIter', 400);
37 #执行优化算法
38 [theta, cost] = ...
39     fminunc(@(t)(costFunction(t, X, y)), init_theta, options);
40   
41   
42 #训练测试
43 predict = X * theta;
44 plot(x, predict);
45 
46 legend('expect','test data','overfiting')

overfiting.m

 

转载于:https://www.cnblogs.com/hikari-1994/p/overfiting-and-regulation.html