【吴恩达机器学习笔记】第四章 正则化
【吴恩达机器学习笔记】第四章 正则化
正则化(Regularization)是一种可以解决过度拟合问题的技术
1、过度拟合问题
我们在拟合过程中可能会出现以下三种情况:
(1)欠拟合

也可以说这个算法具有高偏差,说明它并没有很好的拟合所有数据。
(2)拟合良好
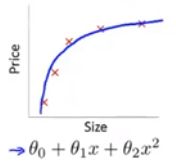
(3)过度拟合
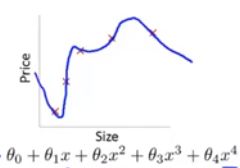
也可以说这个拟合算法具有高方差,如果我们拟合一个多项高阶多项式,那么这个函数几乎能拟合所有的数据,这就可能面临这个函数太过庞大,变量太多的问题,我们没有足够的数据去约束他来获得一个好的假设函数,这就是过度拟合。
概括来说,过度拟合问题将会在变量过多的时候出现,这时训练出的假设能很好的拟合训练集,所以代价函数很可能非常接近于0。但是它会千方百计地去拟合现有数据,导致它无法泛化到新的样本中,无法预测新样本的价格。(泛化:是指一个假设模型应用到新样本的能力)
解决方法:1、减少变量个数 2、正则化:保留全部的变量,但是减少参数的量级。
2、代价函数
正则化的思想是将参数的量级减小,为此我们对所有参数引进了一个惩罚机制,将代价函数修改成如下所示: J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J(\theta )=\frac{1}{2m}[\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}+\lambda \sum_{j=1}^{n}\theta _{j}^{2}] J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]
λ ∑ j = 1 n θ j 2 \lambda \sum_{j=1}^{n}\theta _{j}^{2} λ∑j=1nθj2 被称为正则化项。
λ \lambda λ 被称为正则化参数,其作用为控制两个不同目标之间的取舍,一个目标是更好的拟合数据,第二个目标就是使参数尽可能的小。
如果 λ \lambda λ 取值太大,使参数的惩罚程度太大,会导致各个参数都接近于0。
3、线性回归的正则化
(1)梯度下降算法:
Repeat {
θ 0 : = θ 0 − α [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) \theta _{0}:=\theta _{0}-\alpha [\frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{0}^{(i)} θ0:=θ0−α[m1∑i=1m(hθ(x(i))−y(i))x0(i)
θ j : = θ j − α [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] ( j = 1 , 2 , 3 , . . . , n ) \theta _{j}:=\theta _{j}-\alpha [\frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}+\frac{\lambda }{m}\theta _{j}]\quad(j=1,2,3,...,n) θj:=θj−α[m1∑i=1m(hθ(x(i))−y(i))xj(i)+mλθj](j=1,2,3,...,n)
}
合并后为
Repeat {
θ 0 : = θ 0 − α [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) \theta _{0}:=\theta _{0}-\alpha [\frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{0}^{(i)} θ0:=θ0−α[m1∑i=1m(hθ(x(i))−y(i))x0(i)
θ j : = θ j ( 1 − α λ m ) − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ( j = 1 , 2 , 3 , . . . , n ) \theta _{j}:=\theta _{j}(1-\alpha \frac{\lambda }{m})-\alpha \frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}\quad(j=1,2,3,...,n) θj:=θj(1−αmλ)−αm1∑i=1m(hθ(x(i))−y(i))xj(i)(j=1,2,3,...,n)
}
(2)正规方程法
θ = ( X T X + λ [ 0 1 1 . . . 1 ] ) − 1 X T y \theta =(X^{T}X+\lambda \begin{bmatrix} 0 & & & & \\ & 1& & & \\ & & 1& & \\ & & & ...& \\ & & & & 1 \end{bmatrix})^{-1}X^{T}y θ=(XTX+λ⎣⎢⎢⎢⎢⎡011...1⎦⎥⎥⎥⎥⎤)−1XTy
4、Logistic回归的正则化
(1)梯度下降
Repeat {
θ 0 : = θ 0 − α [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) \theta _{0}:=\theta _{0}-\alpha [\frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{0}^{(i)} θ0:=θ0−α[m1∑i=1m(hθ(x(i))−y(i))x0(i)
θ j : = θ j − α [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] ( j = 1 , 2 , 3 , . . . , n ) \theta _{j}:=\theta _{j}-\alpha [\frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}+\frac{\lambda }{m}\theta _{j}]\quad(j=1,2,3,...,n) θj:=θj−α[m1∑i=1m(hθ(x(i))−y(i))xj(i)+mλθj](j=1,2,3,...,n)
}
与线性回归的非常类似,但是假设函数不一样,为 h θ ( x ) = 1 1 + e − θ T X h_{\theta }(x)=\frac{1}{1+e^{-\theta ^{T}X}} hθ(x)=1+e−θTX1
(2)高级算法
与上一章中的结构相同,只是 J ( θ ) J(\theta ) J(θ) 因加入了参数的惩罚机制而不一样。