tensorflow基础学习—卷积神经网络_卷积层
卷积神经网络中的过滤器，可以将当前层神经网络上的一个节点矩阵转化成下一层神经网络的单位节点矩阵，单位节点矩阵指的是长和宽都为1，但深度不限的节点矩阵。
在一个卷积层中，过滤器所处理的节点矩阵的长和宽都是有人工指定的，这个节点矩阵的尺寸也被称之为过滤器的尺寸。常用的过滤器尺寸有33,或者55.因为过滤器处理的矩阵深度和当前称神经网络节点矩阵的深度一致的，所以虽然节点矩阵是三维的，但过滤器的尺寸只需要指定两个维度，过滤器中另外一个需要人工指定的设置是处理得到的单位矩阵的深度，这个设置被称为过滤前的深度。注意过滤器的尺寸指的是一个过滤器的输入节点的矩阵的大小，而深度指的是输出单位矩阵的深度。
下列展示如将一个223的节点矩阵变化成为一个115的单位节点矩阵，一个过滤器的前向传播过程和全连接层相似，他总共需要223*5+5=65个参数 g ( i ) = f ( ∑ x = 1 2 ∑ y = 1 2 ∑ z = 1 3 a x , y , z × w x , y , z i + b i ) g(i)=f\left(\sum_{x=1}^{2} \sum_{y=1}^{2} \sum_{z=1}^{3} a_{x, y, z} \times w_{x, y, z}^{i}+b^{i}\right) g(i)=f(x=1∑2y=1∑2z=1∑3ax,y,z×wx,y,zi+bi)其中 a x , y , z a_{x, y, z} ax,y,z为过滤节点 ( x , y , z ) (x,y,z) (x,y,z)的取值， f f f为激活函数。
以上样例已经介绍了在卷积层中计算一个过滤器的前向传播过程。卷积层结构的前向传播过程就是通过将一个过滤器从神经网络当前层的左上角移动到右下角，并且在移动中计算每一个对应的单位矩阵得到的。图6-10 展示了卷积层结构前向传播的过程。为了更好
地可视化过滤器的移动过程， 图6-10 中使用的节点矩阵深度都为l 。在图6 - 10 中，展示了在3 × 3 矩阵上使用2 × 2 过滤器的卷积层前传播过程。在这个过程中， 首先将这个过滤器用于左上角子矩阵，然后移动到右上角矩阵， 再到左下角矩阵，最后到右下角矩阵。过滤器每移动一次， 可以计算得到一个值（当深度为k 时会计算出k 个值〉。将这些数值拼接成一个新的矩阵， 就完成了卷积层前向传播的过程。图6- 10 的右侧显示了过滤器在移动过程中计算得到的结果与新矩阵中节点的对应关系。
当过滤器的大小不为l × l 时， 卷积层前向传播得到的矩阵的尺寸要小于当前层矩阵的尺寸。如图6-10 所示， 当前层矩阵的大小为3 × 3 （图6-10 左侧矩阵〉，而通过卷积层前向传播算法之后，得到的矩阵大小为2 × 2 （图6-10 右侧矩阵〉。为了避免尺寸的变化，可以
在当前层矩阵的边界上加入全0 填充 。这样可以使得卷积层前向传播结果矩阵的大小和当前层矩阵保持一致。图6- 1 l 显示了使用全0 填充后卷积层前向传播过程示意图。从医｜中可以看出，加入一层全0填充后，得到的结构矩阵大小就为3 × 3。
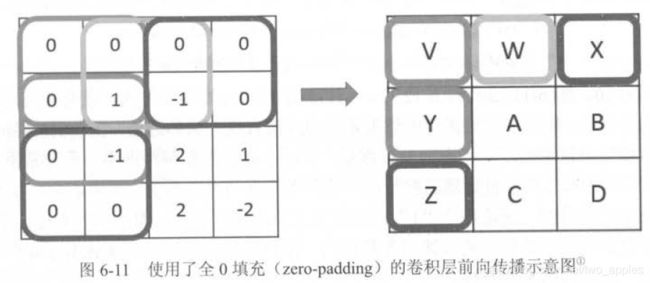
除了使用全0 填充，还可以通过设置过滤器移动的步长来调整结果矩阵的大小。在图6-10 和图6-11 中，过滤器每次都只移动一格。图6-12 中显示了当移动步长为2 且使用全0 填充时，卷积层前向传播的过程。
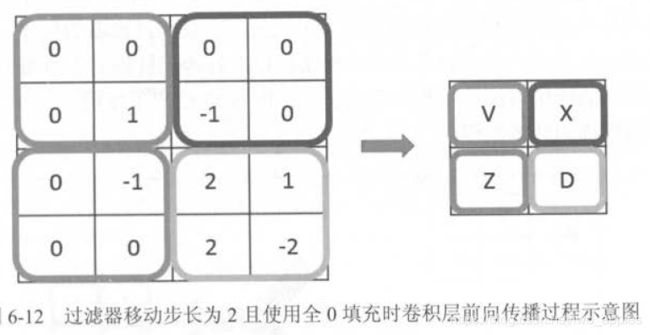以下公式给出了在同时使用全0 填充时结果矩阵的大小： o u t l e n g t h = ⌈ in length / stride length ⌉ \ { out_{length} }=\left\lceil\text { in }_{\text {length}} / \text {stride}_{\text {length}}\right\rceil outlength=⌈ in length/stridelength⌉ o u t w i d t h = ⌈ in width / stride width ⌉ out_{width}=\left\lceil\text { in }_{\text {width}} / \text {stride}_{\text {width}}\right\rceil outwidth=⌈ in width/stridewidth⌉其中 o u t l e n g h out_{lengh} outlengh表示输出层矩阵的宽度，它等于输入层矩阵长度除以长度方向的步长向上取值，宽度与此类推。
当不使用全0填充时， o u t l e n g t h = ⌈ in length − f i l t e r l e n g h + 1 / stride length ⌉ \ { out_{length} }=\left\lceil\text { in }_{\text {length}}-filter_{lengh}+1 / \text {stride}_{\text {length}}\right\rceil outlength=⌈ in length−filterlengh+1/stridelength⌉ o u t w i d t h = ⌈ in width − f i l t e r w i d t h + 1 / stride width ⌉ \ { out_{width} }=\left\lceil\text { in }_{\text {width}}-filter_{width}+1 / \text {stride}_{\text {width}}\right\rceil outwidth=⌈ in width−filterwidth+1/stridewidth⌉在卷积神经网络中，每一个卷积层中使用的过滤器中的参数都是一样的。这是卷积神经网络一个非常重要的性质。从直观上理解，共享过滤器的参数可以使得图像上的内容不受位置的影响。以MNIST手写体数字识别为例，无论数字“ l ”出现在左上角还是右下角，图片的种类都是不变的。因为在左上角和右下角使用的过滤器参数相同，所以通过卷积层之后无论数字在图像上的哪个位置，得到的结果都一样。
共享每一个卷积层中过滤器中的参数可以巨幅减少神经网络上的参数。以CIFAR-10问题为例， 输入层矩阵的维度是3 2x32 巧。假设第一层卷积层使用尺寸为5x5 ，深度为16的过滤器，那么这个卷积层的参数个数为队队队16+16=1216 个。6.2 节中提到过，使用500
个隐藏节点的全连接层将有1. 5 百万个参数。相比之下，卷积层的参数个数要远远小于全连接层。而且卷积层的参数个数和图片的大小无关，它只和过滤器的尺寸、深度以及当前层节点矩阵的深度有关。这使得卷积神经网络可以很好地扩展到更大的图像数据上。
TensorFlow 对卷积神经网络提供了非常好的支持，以下程序实现了一个卷积层的前向传播过程。从以下代码可以看出，通过TensorFlow 实现卷积层是非常方便的
import tensorflow as tf
from tensorflow.python.platform import gfile
#通过tf.get_variable的方式创建过滤器的权重变量和偏置想变量
#卷积层的参数个数只和过滤器的尺寸、深度以及当前层节点的的深
#度有关，所以这里申明的参数变量是一个四维矩阵，前面两个参数
#代表了过滤器的尺寸，第三个维度表示当前层的深度，第四个
#维度表示过滤器的深度。
fileter_weight=tf.get_variable(
"weight",[5,5,3,16],
initializer=tf.truncated_normal_initializer(stddev=0.1)
)
#和卷积层的权重类似，当前层矩阵上不同位置的偏置项也是共享的，
#所以总共有下一层深度个不同的偏置项。本样例代码中16为过滤器的
#深度，也是神经网络中下一层节点矩阵的深度。
#tf.nn.conv2d 提供了一个非常方便的函数来实现卷积层的前向传播算法
#这个函数的第一个输入为当前层的节点矩阵。注意这个矩阵是一个四维矩
#阵，后面三个维度对应一个节点矩阵，第一维度对应对应一个输入batch.
#比如在输入层，input[0,:,:,:]表示第一张图片，input[1,:,:,:]表
#示第二张图片，以此类推，tf.nn.conv2d第二个参数提供了卷积层的权重
#第三个参数为不同维度上的步长。虽然第三个参数提供的是一个长度为4
#的数组，但是第一维和最后一维的数字要求一定是l 。这是因为卷积层
#的步长只对矩阵的长和宽有效。最后一个参数是填充的方法。
#tensorflow中提供SAME或是VALID两种选择，其中SAME表示添加全0填充
#"VALID"表示不添加
conv=tf.nn.conv2d(
input,filter_weight,strides=[1,1,1,1],padding='SAME'
)
#tf.nn.bias_add 提供了一个方便的函数给每一个节点添加偏置项，这里
#不能直接使用加法，因为矩阵上不同位置上的节点都需要加上同样的偏置项
#虽然下一层神经网络的大小为2*2矩阵中的每一个值都需要加上一个偏置项
bias=tf.nn.bias_add(conv,biases)
#将计算结果通过ReLU激活函数完成去线性化
actived_conv=tf.nn.relu(bias)