逻辑回归（Logistic Regression）通俗解释

【机器学习】逻辑回归（Logistic Regression）

注：最近开始学习《人工智能》选修课，老师提纲挈领的介绍了一番，听完课只了解了个大概，剩下的细节只能自己继续摸索。

从本质上讲：机器学习就是一个模型对外界的刺激（训练样本）做出反应，趋利避害（评价标准）。

1. 什么是逻辑回归？

---

许多人对线性回归都比较熟悉，但知道逻辑回归的人可能就要少的多。从大的类别上来说，逻辑回归是一种有监督的统计学习方法，主要用于对样本进行分类。

在线性回归模型中，输出一般是连续的，例如

y=f(x)=ax+by=f(x)=ax+b

，对于每一个输入的x，都有一个对应的y输出。模型的定义域和值域都可以是[-∞, +∞]。但是对于逻辑回归，输入可以是连续的[-∞, +∞]，但输出一般是离散的，即只有有限多个输出值。例如，其值域可以只有两个值{0, 1}，这两个值可以表示对样本的某种分类，高/低、患病/健康、阴性/阳性等，这就是最常见的二分类逻辑回归。因此，从整体上来说，通过逻辑回归模型，我们将在整个实数范围上的x映射到了有限个点上，这样就实现了对x的分类。因为每次拿过来一个x，经过逻辑回归分析，就可以将它归入某一类y中。

逻辑回归与线性回归的关系

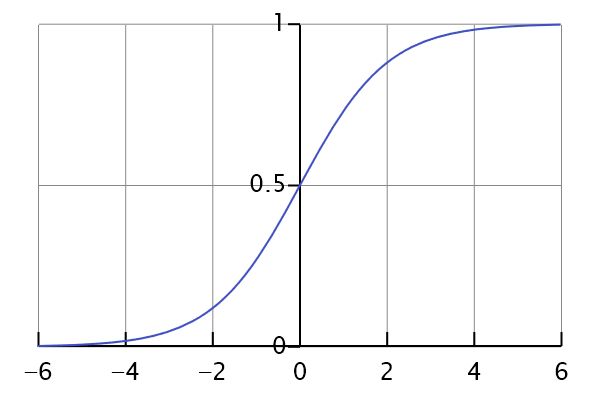
逻辑回归也被称为广义线性回归模型，它与线性回归模型的形式基本上相同，都具有 ax+b，其中a和b是待求参数，其区别在于他们的因变量不同，多重线性回归直接将ax+b作为因变量，即y = ax+b，而logistic回归则通过函数S将ax+b对应到一个隐状态p，p = S(ax+b)，然后根据p与1-p的大小决定因变量的值。这里的函数S就是Sigmoid函数

S(t)=11+e−tS(t)=11+e−t

将t换成ax+b，可以得到逻辑回归模型的参数形式：

p(x;a,b)=11+e−(ax+b)……（1）p(x;a,b)=11+e−(ax+b)……（1）

 

图1：sigmoid函数的图像

通过函数S的作用，我们可以将输出的值限制在区间[0， 1]上，p(x)则可以用来表示概率p(y=1|x)，即当一个x发生时，y被分到1那一组的概率。可是，等等，我们上面说y只有两种取值，但是这里却出现了一个区间[0, 1]，这是什么鬼？？其实在真实情况下，我们最终得到的y的值是在[0, 1]这个区间上的一个数，然后我们可以选择一个阈值，通常是0.5，当y>0.5时，就将这个x归到1这一类，如果y<0.5就将x归到0这一类。但是阈值是可以调整的，比如说一个比较保守的人，可能将阈值设为0.9，也就是说有超过90%的把握，才相信这个x属于1这一类。了解一个算法，最好的办法就是自己从头实现一次。下面是逻辑回归的具体实现。

逻辑回归模型的代价函数

逻辑回归一般使用交叉熵作为代价函数。关于代价函数的具体细节，请参考代价函数，这里只给出交叉熵公式：

J(θ)=−1m[∑i=1m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]J(θ)=−1m[∑i=1m(y(i)log⁡hθ(x(i))+(1−y(i))log⁡(1−hθ(x(i)))]

m：训练样本的个数；

hθ(x)：用参数θ和x预测出来的y值；

y：原训练样本中的y值，也就是标准答案

上角标(i)：第i个样本

2. 数据准备

---

下面的数据来自《机器学习实战》中的示例：

-0.017612	14.053064	0
-1.395634	4.662541	1
-0.752157	6.538620	0
-1.322371	7.152853	0
0.423363	11.054677	0
0.406704	7.067335	1
0.667394	12.741452	0
-2.460150	6.866805	1
0.569411	9.548755	0
-0.026632	10.427743	0

上面的数据一共是3列10行，其中前两列为x1和x2的值，第3列表示y的值；10行表示取了10个样本点。我们可以将这些数据当做训练模型参数的训练样本。

见到训练样本就可以比较直观的理解算法的输入，以及我们如何利用这些数据来训练逻辑回归分类器，进而用训练好的模型来预测新的样本（检测样本）。

从逻辑回归的参数形式，式子（1）我们可以看到逻辑回归模型中有两个待定参数a（x的系数）和b（常数项），我们现在给出来的数据有两个特征x1, x2，因此整个模型就增加了一项：ax1 + cx2 + b。为了形式上的统一，我们使用带下标的a表示不同的参数（a0表示常数项b并作x0的参数，a1、a2分别表示x1和x2的参数），就可以得到：

a0x0+a1x1+a2x2a0x0+a1x1+a2x2

 

这样统一起来后，就可以使用矩阵表示了（比起前面展开的线性表示方式，用矩阵表示模型和参数更加简便，而且矩阵运算的速度也更快）：

[a0a1a2]⎡⎣⎢x0x1x2⎤⎦⎥=aTX[a0a1a2][x0x1x2]=aTX

 将上面的式子带入到（1）式，我们就可以得到逻辑回归的另一种表示形式了：

p(x;a)=11+e−aTX……（2）p(x;a)=11+e−aTX……（2）

 此时，可以很清楚的看到，我们后面的行动都是为了确定一个合适的a（一个参数向量），使得对于一个新来的X（也是一个向量），我们可以尽可能准确的给出一个y值，0或者1.

注：数据是二维的，也就是说这组观察样本中有两个自变量，即两个特征（feature）。

3. 训练分类器

---

就像上面说的，训练分类器的过程，就是根据已经知道的数据（训练样本）确定一个使得代价函数的值最小的a（参数向量/回归系数）的过程。逻辑回归模型属于有监督的学习方法，上面示例数据中的第3列其实是训练样本提供的"标准答案"。也就是说，这些数据是已经分好类的（两类，0或者1）。在训练阶段，我们要做的就是利用训练样本和（2）式中的模型，估计一个比较合适的参数a，使得仅通过前面两列数据（观察值/测量值）就可以估计一个值h(a)，这个值越接近标准答案y，说明我们的模型预测的越准确。

下面是估计回归系数a的值的过程，还是借鉴了《机器学习实战》中的代码，做了少量修改：

其中计算参数梯度，即代价函数对每个参数的偏导数（下面代码中的第36-38行），的详细推导过程可以参考这里

 1 '''
 2 Created on Oct 27, 2010
 3 Logistic Regression Working Module
 4 @author: Peter
 5 '''
 6 from numpy import *
 7 import os
 8 
 9 path = 'D:\MechineLearning\MLiA_SourceCode\machinelearninginaction\Ch05'
10 training_sample = 'trainingSample.txt'
11 testing_sample = 'testingSample.txt'
12 
13 # 从文件中读入训练样本的数据，同上面给出的示例数据
14 # 下面第20行代码中的1.0表示x0 = 1
15 def loadDataSet(p, file_n):
16     dataMat = []; labelMat = []
17     fr = open(os.path.join(p, file_n))
18     for line in fr.readlines():
19         lineArr = line.strip().split()
20         dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])  # 三个特征x0, x1, x2
21         labelMat.append(int(lineArr[2]))  # 标准答案y
22     return dataMat,labelMat
23 
24 def sigmoid(inX):
25     return 1.0/(1+exp(-inX))
26 
27 # 梯度下降法求回归系数a，由于样本量少，我将迭代次数改成了1000次
28 def gradAscent(dataMatIn, classLabels):
29     dataMatrix = mat(dataMatIn)             #convert to NumPy matrix
30     labelMat = mat(classLabels).transpose() #convert to NumPy matrix
31     m,n = shape(dataMatrix)
32     alpha = 0.001  # 学习率
33     maxCycles = 1000
34     weights = ones((n,1))
35     for k in range(maxCycles):              # heavy on matrix operations
36         h = sigmoid(dataMatrix*weights)     # 模型预测值, 90 x 1
37         error = h - labelMat                # 真实值与预测值之间的误差, 90 x 1
38         temp = dataMatrix.transpose()* error # 交叉熵代价函数对所有参数的偏导数, 3 x 1
39         weights = weights - alpha * temp  # 更新权重
40     return weights
41 
42 # 下面是我自己写的测试函数
43 def test_logistic_regression():
44     dataArr, labelMat = loadDataSet(path, training_sample)  # 读入训练样本中的原始数据
45     A = gradAscent(dataArr, labelMat)  # 回归系数a的值
46     h = sigmoid(mat(dataArr)*A)  #预测结果h(a)的值
47     print(dataArr, labelMat)
48     print(A)
49     print(h)
50     # plotBestFit(A.getA())
51 
52 test_logistic_regression()

上面代码的输出如下：

• 一个元组，包含两个数组：第一个数组是所有的训练样本中的观察值，也就是X，包括x0, x1, x2；第二个数组是每组观察值对应的标准答案y。

([[1.0, -0.017612, 14.053064], [1.0, -1.395634, 4.662541], [1.0, -0.752157, 6.53862], [1.0, -1.322371, 7.152853], [1.0, 0.423363, 11.054677], [1.0, 0.406704, 7.067335], [1.0, 0.667394, 12.741452], [1.0, -2.46015, 6.866805], [1.0, 0.569411, 9.548755], [1.0, -0.026632, 10.427743]], [0, 1, 0, 0, 0, 1, 0, 1, 0, 0])  

• 本次预测出来的回归系数a，包括a0, a1, a2

[[ 1.39174871]
[-0.5227482 ]
[-0.33100373]]  

• 根据回归系数a和（2）式中的模型预测出来的h(a)。这里预测得到的结果都是区间(0, 1)上的实数。

[[ 0.03730313]
[ 0.64060602]
[ 0.40627881]
[ 0.4293251 ]
[ 0.07665396]
[ 0.23863652]
[ 0.0401329 ]
[ 0.59985228]
[ 0.11238742]
[ 0.11446212]]  

标准答案是{0, 1}，如何将预测到的结果与标准答案y进行比较呢？取0.5作为阈值，大于该值的样本就划分到1这一组，小于等于该值的样本就划分到0这一组，这样就可以将数据分为两类。检查一下结果可以看到，我们现在分出来的1这一类中包括原来y=1的两个样本，另一类包括原来y=0的所有样本和一个y=1的样本（分错了）。鉴于我们选择取的样本比较少（只有10个），这样的效果其实还算非常不错的！

 4. 结果展示

---

上面已经求出了一组回归系数，它确定了不同类别数据之间的分割线。可以利用X内部（x1与x2之间的关系）的关系画出该分割线，从而更直观的感受到分类的效果。

添加下面一段代码：

 1 # 分类效果展示，参数weights就是回归系数
 2 def plotBestFit(weights):
 3     import matplotlib.pyplot as plt
 4     dataMat,labelMat=loadDataSet()
 5     dataArr = array(dataMat)
 6     n = shape(dataArr)[0]
 7     xcord1 = []; ycord1 = []
 8     xcord2 = []; ycord2 = []
 9     for i in range(n):
10         if int(labelMat[i])== 1:
11             xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
12         else:
13             xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
14     fig = plt.figure()
15     ax = fig.add_subplot(111)
16     ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
17     ax.scatter(xcord2, ycord2, s=30, c='green')
18     x = arange(-3.0, 3.0, 0.1)
19     y = (-weights[0]-weights[1]*x)/weights[2]  # x2 = f(x1)
20     ax.plot(x, y)
21     plt.xlabel('X1'); plt.ylabel('X2');
22     plt.show()

将上面的test_logistic_regression()函数中的最后一句注释去掉，调用plotBestFit函数就可以看到分类的效果了。

这里说明一下上面代码中的第19行，这里设置了sigmoid函数的取值为1/2，也就是说取阈值为0.5来划分最后预测的结果。这样可以得到

e−aTX=1e−aTX=1

，即-aTX=0，可以推出x2 = (-a0x0 - a1x1)/a2，同第19行，也就是说这里的y实际上是x2，而x是x1。因此下图表示的是x1与x2之间的关系。

分类效果图如下：

三个红色的点是原来y=1的样本，有一个分错了。这里相当于将所有的数据用二维坐标(x1, x2)表示了出来，而且根据回归参数画出的线将这些点一分为二。如果有新的样本，不知道在哪一类，只用将该点画在图上，看它在这条直线的哪一边就可以分类了。

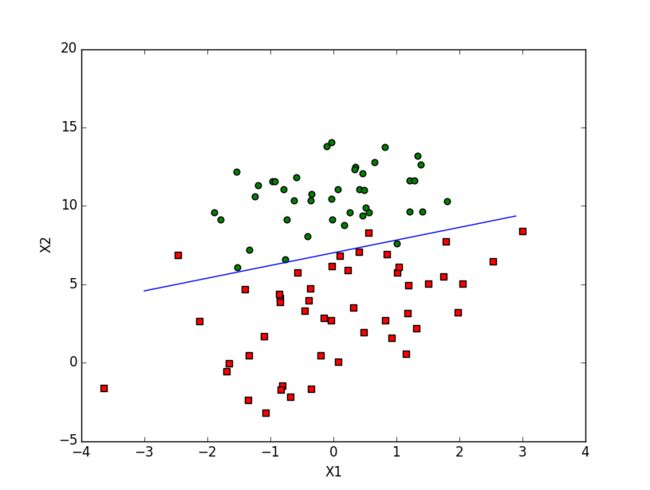
下面是使用90个训练样本得到的结果：

可以看出一个非常明显的规律是，y=1的这一类样本（红色的点）具有更小的x2值，当x2相近时则具有更大的x1值。

此时计算出来的回归系数a为：

[[ 5.262118 ]
[ 0.60847797]
[-0.75168429]]

5. 预测新样本

---

添加一个预测函数，如下：

直接将上面计算出来的回归系数a拿来使用，测试数据其实也是《机器学习实战》这本书中的训练数据，我拆成了两份，前面90行用来做训练数据，后面10行用来当测试数据。

1 def predict_test_sample():
2     A = [5.262118, 0.60847797, -0.75168429]  # 上面计算出来的回归系数a
3     dataArr, labelMat = loadDataSet(path, testing_sample)  
4     h_test = sigmoid(mat(dataArr) * mat(A).transpose())  # 将读入的数据和A转化成numpy中的矩阵
5     print(h_test)  # 预测的结果

调用上面的函数，可以得到以下结果，即h(a)：

[[ 0.99714035]
[ 0.04035907]
[ 0.12535895]
[ 0.99048731]
[ 0.98075409]
[ 0.97708653]
[ 0.09004989]
[ 0.97884487]
[ 0.28594188]
[ 0.00359693]]

下面是我们的测试数据（原来的训练样本后十行的数据，包括标准答案y）：

0.089392	-0.715300	1
1.825662	12.693808	0
0.197445	9.744638	0
0.126117	0.922311	1
-0.679797	1.220530	1
0.677983	2.556666	1
0.761349	10.693862	0
-2.168791	0.143632	1
1.388610	9.341997	0
0.317029	14.739025	0

比较我们预测得到的h(a)和标准答案y，如果按照0.5为分界线的话，我们利用前90个样本训练出来的分类器对后面10个样本的类型预测全部正确。

附件：

完整代码：https://github.com/OnlyBelter/MachineLearning_examples/tree/master/de_novo/regression

训练数据：https://github.com/OnlyBelter/MachineLearning_examples/blob/master/de_novo/data/Logistic_Regression-trainingSample.txt

测试数据：https://github.com/OnlyBelter/MachineLearning_examples/blob/master/de_novo/data/Logistic_Regression-testingSample.txt

参考：

http://baike.baidu.com/item/logistic%E5%9B%9E%E5%BD%92

https://en.wikipedia.org/wiki/Sigmoid_function

《机器学习实战》，哈林顿著，李锐等译，人民邮电出版社，2013年6月第一版